Đa thức một biến
Chuyên đề: Đa thức một biến
Chuyên đề Toán 7 Đa thức một biến được VnDoc gửi tới các bạn học sinh cùng quý thầy cô tham khảo.
A. Lý thuyết Đa thức một biến
1. Đa thức một biến là gì?
• Đa thức một biến là tổng của những đơn thức của cùng một biến.
• Một số được coi là một đơn thức một biến.
• Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.
Ví dụ: Đa thức 5x5 + 4x3 – 2x2 + x là đa thức một biến (biến x); bậc của đa thức là 5.
2. Sắp xếp một đa thức một biến
– Để thuận lợi cho việc tính toán đối với các đa thức một biến, người ta thường sắp xếp các hạng tử của chúng theo lũy thừa tăng hoặc giảm của biến.
Ví dụ 1: Đối với đa thức P(x) = 6x + 3 – 6x2 + x3 + 2x4
+ Khi sắp xếp các hạng tử của nó theo lũy thừa giảm của biến, ta được:
P(x) = 2x4 + x3 – 6x2 + 6x + 3
+ Khi sắp xếp các hạng tử của nó theo lũy thừa tăng của biến, ta được:
P(x) = 3 + 6x – 6x2 + x3 + 2x4
– Nhận xét: Mọi đa thức bậc 2 của biến x, sau khi đã sắp xếp các hạng tử của chúng theo lũy thừa giảm của biến, đều có dạng: ax2 + bx + c
Trong đó a, b, c là các số cho trước và a ≠ 0.
– Chú ý:
• Để sắp xếp các hạng tử của một đa thức, trước hết ta phải thu gọn đa thức đó.
• Những chữ đại diện cho các số xác định cho trước được goi là hằng số.
Ví dụ 2: Cho đa thức P(x) = 2 + 5x2 – 3x3 + 4x – 2x – x3 + 6x5. Thu gọn và sắp xếp đa thức.
P(x) = 2 + 5x2 – 3x3 + 4x2 – 2x – x3 + 6x5
= 6x5 + (– 3x3 – x3) + (5x2 + 4x2) – 2x + 2
= 6x5 – 4x3 + 9x2 – 2x + 2
3. Hệ số
– Hệ số của lũy thừa 0 của biến gọi là hệ số tự do; hệ số của lũy thừa cao nhất của biến gọi là hệ số cao nhất.
Ví dụ 3: Các hệ số của đa thức 6x5 – x4 + 5x2 – x + 2 là: 6; – 1; 5; – 1; 2
Hệ số tự do là: 2
Hệ số cao nhất là: 6
B. Bài tập đa thức một biến
I. Câu hỏi trắc nghiệm
Bài 1: Đa thức nào dưới đây là đa thức một biến?
|
A. x2 + y + 1 B. x3 – 2x2 + 3 |
C. xy + x2 – 3 D. xyz – yz + 3 |
Lời giải:
Đa thức x3 – 2x2 + 3 là đa thức một biến
Chọn đáp án B
Bài 2: Sắp xếp 6x3 + 5x4 – 8x6 – 3x2 + 4 theo lũy thừa giảm dần của biến ta được:
A. – 8x6 + 5x4 + 6x3 – 3x2 + 4
B. – 8x6 – 5x4 + 6x3 – 3x2 + 4
C. 8x6 + 5x4 + 6x3 – 3x2 + 4
D. 8x6 + 5x4 + 6x3 + 3x2 + 4
Ta có: 6x3 + 5x4 – 8x6 – 3x2 + 4
= – 8x6 + 5x4 + 6x3 – 3x2 + 4
Chọn đáp án A
Bài 3: Đa thức 7x12 – 8x10 + x11 – x5 + 6x6 + x – 10 được sắp xếp theo lũy thừa tăng dần của biến ta được:
A. – 10 + x + x5 + 6x6 – 8x10 + x11 + 7x12
B. 10 + x + x5 + 6x6 – 8x10 + x11 + 7x12
C. 10 + x – x5 + 6x6 – 8x10 + x11 + 7x12
D. – 10 + x – x5 + 6x6 – 8x10 + x11 + 7x12
Ta có: 7x12 – 8x10 + x11 – x5 + 6x6 + x – 10
= – 10 + x – x5 + 6x6 – 8x10 + x11 + 7x12
Chọn đáp án D
Bài 4: Với a, b, c là các hằng số, hệ số tự do của đa thức x2 + (a + b)x – 5a + 3b + 2 là:
|
A. 5a + 3b + 2 B. – 5a + 3b + 2 |
C. 2 D. 3b + 2 |
Hệ số tự do của đa thức x2 + (a + b)x – 5a + 3b + 2 là: – 5a + 3b + 2
Chọn đáp án B
Bài 5: Hệ số cao nhất của đa thức 5x6 + 6x5 + x4 – 3x2 + 7 là:
| A. 6 | B. 7 | C. 4 | D. 5 |
Hệ số cao nhất của đa thức 5x6 + 6x5 + x4 – 3x2 + 7 là: 5
Chọn đáp án D
Bài 6: Cho đa thức A = x4 – 4x3 + x – 3x2 + 1. Tính giá trị của A tại x = – 2
|
A. A = – 35 B. A = 53 |
C. A = 33 D. A = 35 |
Thay x = – 2 vào biểu thức A , ta có
A = (– 2)4 – 4.(– 2)3 + (– 2) – 3.(– 2)2 + 1
= 16 + 32 – 2 – 12 + 1 = 35
Vậy với x = – 2 thì A = 35
Chọn đáp án D
Câu 7: Hệ số cao nhất của đa thức – 7x5 – 9x2 + x6 – x4 + 10
| A. – 7 | B. – 1 | C. 10 | D. 1 |
Đáp án cần chọn là: D
Ta có: – 7x5 – 9x2 + x6 – x4 + 10= x6 – 7x5 – x4 – 9x2 + 10
Hệ số cao nhất của đa thức đã cho là 1
Câu 8: Cho đa thức – 3x2 + 5x6 – 7x. Tính giá trị của A tại x = – 1
|
A. A = – 9 B. A = – 15 |
C. A = – 5 D. A = 9 |
Đáp án cần chọn là: D
Thay x = – 1 vào đa thức A ta được:
A = – 3.(–1)2 + 5.(– 1)6 – 7.(– 1) = – 3 + 5 + 7 = 9
Vậy với x = – 1 thì A = 9
Câu 9: Bậc của đa thức 8x8 – x2 + x9 + x5 – 12x3 + 10 là
| A. 10 | B. 8 | C. 9 | D. 7 |
Đáp án cần chọn là: C
Ta có số mũ cao nhất của biến trong đa thức
8x8 – x2 + x9 + x5 – 12x3 + 10 là 9 nên bậc của đa thức 8x8 – x2 + x9 + x5 – 12x3 + 10 là 9
Câu 10: Bậc của đa thức 9x2 + x7 – x5 + 1 là:
| A. 14 | B. 9 | C. 5 | D. 7 |
Đáp án cần chọn là: D
Ta có số mũ cao nhất của biến trong đa thức
9x2 + x7 – x5 + 1 là 7 nên bậc của đa thức 9x2 + x7 – x5 + 1 là 7
II. Bài tập tự luận
Bài 1: Thu gọn các đa thức sau và sắp xếp theo lũy thừa giảm dần của biến
a) 2x3 – x5 + 3x4 + x2 – (1/2)x3 + 3x5 – 2x2 – x4 + 1
b) x7 – 3x4 + 2x3 – x2 – x4 – x + x7 – x3 + 5
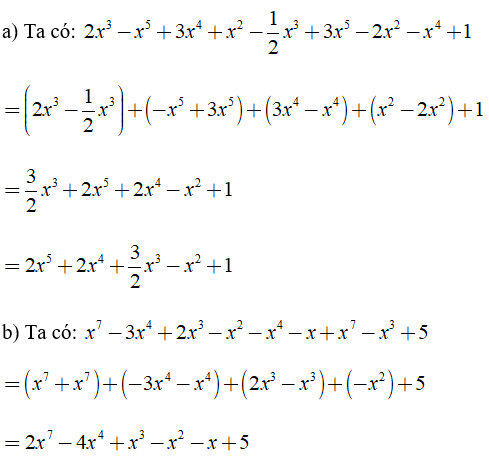
Bài 2: Tính giá trị của các biểu thức sau:
a) x + x2 + x3 + x4 + .... + x99 + x100 tại x = – 1
b) x2 + x4 + x6 + .... + x98 + x100 tại x = – 1
Đáp án
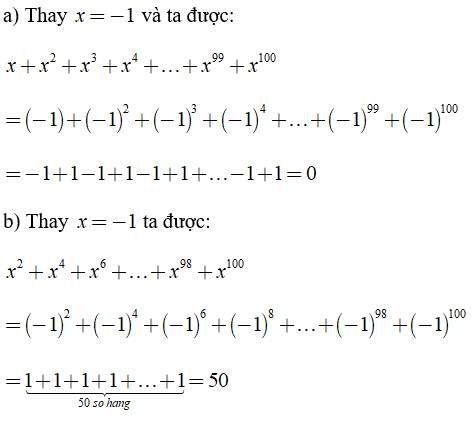
Bài 3: Cho đa thức: A(x) = – 2x2 + 3x – x4 + 5 + 3x2 – 4x
a) Thu gọn, sắp xếp các hạng tử theo lũy thừa giảm của biến.
b) Xác định các hệ số của các đa thức.
Bài 4: Cho đa thức ax4 – 2x3 + 3x2 – 2x4 – 7x +1. Biết rằng đa thức này có bậc bằng 4 và a là số nguyên tố nhỏ hơn 5. Tìm a.
..........................







