Toán 7 Bài 28: Phép chia đa thức một biến
Giải Toán 7 KNTT tập 2 trang 43
Giải Toán 7 Bài 28: Phép chia đa thức một biến sách Kết nối tri thức hướng dẫn giải bài tập trong SGK Toán 7 Kết nối tri thức tập 2 trang 40, 41 42, 43, giúp các em học sinh ôn tập, củng cố kiến thức được học trong bài 28 Toán 7 KNTT. Sau đây mời các bạn tham khảo chi tiết.
1. Làm quen với phép chia đa thức
HĐ1 trang 40 Toán 7 Tập 2: Tìm thương của mỗi phép chia hết sau:
a) 12x3 : 4x;
b) (-2x4) : x4;
c) 2x5 : 5x2.
Hướng dẫn giải:
a) 12x3 : 4x = (12 : 4). (x3 : x) = 3x2.
b) (-2x4) : x4 = (-2). (x4 : x4) = -2.
c) 2x5 : 5x2 = (2 : 5). (x5 : x2) = x3.
Luyện tập 1 trang 40 Toán 7 Tập 2: Thực hiện các phép chia sau:
a) 3x7 : x4;
b) (-2x) : x;
c) 0,25x5 : (-5x2).
Hướng dẫn giải:
a) 3x7 : x4 = (3 : ). (x7 : x4) = 3.2.x3 = 6x3.
b) (-2x) : x = -2. (x : x) = -2.
c) 0,25x5 : (-5x2) = [0,25 : (-5)]. (x5 : x2) = -0,05x3.
2. Chia đa thức cho đa thức, trường hợp chia hết
Câu hỏi trang 41 Toán 7 Tập 2: Kiểm tra lại rằng ta có phép chia hết A : B = 2x2 - 5x + 1, nghĩa là xảy ra
A = B . (2x2 - 5x + 1).
Hướng dẫn giải:
Ta có B . (2x2 - 5x + 1) = (x2 - 4x - 3) . (2x2 - 5x + 1)
= x2.(2x2 - 5x + 1) + (-4x).(2x2 - 5x + 1) + (-3).(2x2 - 5x + 1)
= x2 . 2x2 + x2 . (-5x) + x2 . 1 + (-4x) . 2x2 + (-4x) . (-5x) + (-4x) . 1 + (-3) . 2x2
+ (-3) . (-5x) + (-3) . 1
= 2x4 - 5x3 + x2 - 8x3 + 20x2 - 4x - 6x2 + 15x - 3
= 2x4 + (-5x3 - 8x3) + (x2 + 20x2 - 6x2) + (-4x + 15x) - 3
= 2x4 - 13x3 + 15x2 + 11x - 3
= A.
Vậy ta có phép chia hết A : B = 2x2 - 5x + 1.
Luyện tập 2 trang 41 Toán 7 Tập 2: Thực hiện phép chia:
a) (-x6 + 5x4 - 2x3) : 0,5x2.
b) (9x2 - 4) : (3x + 2).
Hướng dẫn giải:
a) (-x6 + 5x4 - 2x3) : 0,5x2
= -x6 : 0,5x2 + 5x4 : 0,5x2 + (-2x3) : 0,5x2
= (-1 : 0,5) . (x6 : x2) + (5 : 0,5) . (x4 : x2) + (-2 : 0,5) . (x3 : x2)
= (-1 : )x4 + (5 : )x2 + (-2 : )x
= (-1 . 2)x4 + (5 . 2)x2 + (-2 . 2)x
= -2x4 + 10x2 - 4x
b) Thực hiện theo các bước sau:
Bước 1. Lấy hạng tử có bậc cao nhất của đa thức 9x2 - 4 chia cho hạng tử có bậc cao nhất của đa thức 3x + 2:
9x2 : 3x = 3x.
Bước 2. Lấy đa thức 9x2 - 4 trừ đi (3x + 2).3x ta được dư thứ nhất là -6x - 4.
Bước 3. Lấy hạng tử có bậc cao nhất của dư thứ nhất chia cho hạng tử có bậc cao nhất của đa thức 3x + 2:
-6x : 3x = -2.
Bước 4. Lấy dư thứ nhất trừ đi -2(3x + 2) ta được dư thứ hai là 0 nên quá trình chia kết thúc.
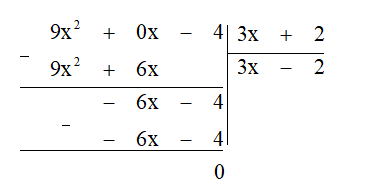
Vậy (9x2 - 4) : (3x + 2) = 3x - 2.
Vận dụng trang 41 Toán 7 Tập 2: Em hãy giải bài toán trong tình huống mở đầu
Hướng dẫn giải:
Thực hiện theo các bước sau:
Bước 1. Lấy hạng tử có bậc cao nhất của A chia cho hạng tử có bậc cao nhất của B:
2x4 : x2 = 2x2.
Bước 2. Lấy A trừ đi tích B. 2x2 ta được dư thứ nhất là -3x3 + x2 + 6x - 2.
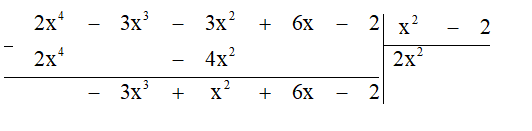
Bước 3. Lấy hạng tử cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:
(-3x3) : x2 = -3x.
Bước 4. Lấy dư thứ nhất trừ đi tích B. (-3x) ta được dư thứ hai là x2 - 2.
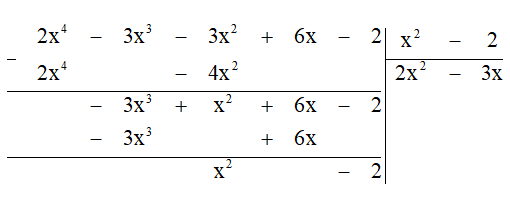
Bước 5. Lấy hạng tử cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:
x2 : x2 = 1.
Bước 6. Lấy dư thứ nhất trừ đi tích B. 1 ta được dư thứ ba là 0.
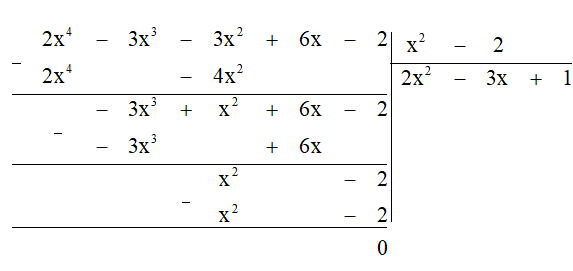
Bước 7. Dư cuối cùng bằng 0 nên quá trình chia kết thúc.
Vậy A : B = 2x2 - 3x + 1.
Bài tập
Bài 7.30 trang 43 SGK Toán 7 tập 2 KNTT
Tính:
a) 8x5 : 4x3
b) 120x7 : (-24x5)
c) ![]() \(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x\)
\(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x\)
d) -3,72x 4 : (-4x 2)
Hướng dẫn giải:
a) 8x5 : 4x3 = (8 : 4) . (x5 : x3) = 2.x2
b) 120x7 : (-24x5) = [120 : (-24)] . (x7 : x5) = -5.x2
c) ![]() \(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x = \dfrac{{ - 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ - 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = - 6{x^2}\)
\(\dfrac{3}{4}{( - x)^3}:\dfrac{1}{8}x = \dfrac{{ - 3}}{4}{x^3}:\dfrac{1}{8}x = \left( {\dfrac{{ - 3}}{4}:\dfrac{1}{8}} \right).({x^3}:x) = - 6{x^2}\)
d) -3,72x 4 : (-4x 2 ) = [(-3,72) : (-4)] . (x 4 : x 2 ) = 0,93x 2
Bài 7.31 trang 43 SGK Toán 7 tập 2 KNTT
Thực hiện các phép chia đa thức sau:
a) ![]() \((-5x^3 + 15x^2 + 18x) : (-5x)\);
\((-5x^3 + 15x^2 + 18x) : (-5x)\);
b) ![]() \((-2x^5 – 4x^3 + 3x^2) : 2x^2\).
\((-2x^5 – 4x^3 + 3x^2) : 2x^2\).
Hướng dẫn giải:
a) ![]() \((-5x^3 + 15x^2 + 18x) : (-5x)\)
\((-5x^3 + 15x^2 + 18x) : (-5x)\)
![]() \(= (-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)\)
\(= (-5x^3) : (-5x) + 15x^2 : (-5x) + 18x : (-5x)\)
![]() \(= x^2 – 3x - \frac{18}{5}\)
\(= x^2 – 3x - \frac{18}{5}\)
b) ![]() \((-2x^5 – 4x^3 + 3x^2) : 2x^2\)
\((-2x^5 – 4x^3 + 3x^2) : 2x^2\)
![]() \(= (-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)\)
\(= (-2x^5 : 2x^2) + (-4x^3 : 2x^2) + (3x^2 : 2x^2)\)
![]() \(= -x^3 – 2x - \frac{3}{2}\)
\(= -x^3 – 2x - \frac{3}{2}\)
Bài 7.32 trang 43 SGK Toán 7 tập 2 KNTT
Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:
a) ![]() \((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
\((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
b) ![]() \((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
\((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
Hướng dẫn giải:
a) ![]() \((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
\((6x^3 – 2x^2 – 9x + 3) : (3x – 1)\);
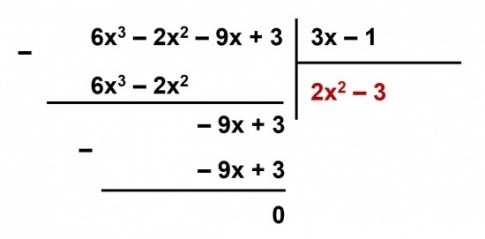
b) ![]() \((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
\((4x^4 + 14x^3 – 21x – 9) : (2x^2 – 3)\).
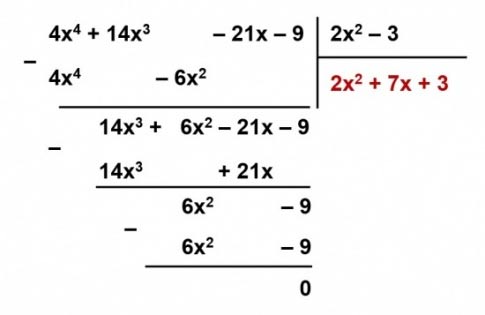
Bài 7.33 trang 43 SGK Toán 7 tập 2 KNTT
Thực hiện phép chia ![]() \(0,5x^5 + 3,2x^3 – 2x^2\) cho
\(0,5x^5 + 3,2x^3 – 2x^2\) cho ![]() \(0,25x^n\) trong mỗi trường hợp sau:
\(0,25x^n\) trong mỗi trường hợp sau:
a) n = 2;
b) n = 3.
Hướng dẫn giải:
a) n = 2
![]() \((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2\)
\((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^2\)
![]() \(= (0,5x^5 : 0,25x^2) + (3,2x^3 : 0,25x^2) + (– 2x^2 : 0,25x^2)\)
\(= (0,5x^5 : 0,25x^2) + (3,2x^3 : 0,25x^2) + (– 2x^2 : 0,25x^2)\)
![]() \(= 2x^3 + 12,8x - 8\)
\(= 2x^3 + 12,8x - 8\)
b) n = 3
![]() \((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^3\)
\((0,5x^5 + 3,2x^3 – 2x^2) : 0,25x^3\)
![]() \(= (0,5x^5 : 0,25x^3) + (3,2x^3 : 0,25x^3) + (– 2x^2 : 0,25x^3)\)
\(= (0,5x^5 : 0,25x^3) + (3,2x^3 : 0,25x^3) + (– 2x^2 : 0,25x^3)\)
![]() \(= 2x^2 + 12,8 - \frac{8}{x}\)
\(= 2x^2 + 12,8 - \frac{8}{x}\)
Bài 7.34 trang 43 SGK Toán 7 tập 2 KNTT
Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng:
F(x) = G(x) . Q(x) + R(x).
a) ![]() \(F(x) = 6x^4 – 3x^3 + 15x^2 + 2x – 1; G(x) = 3x^2\).
\(F(x) = 6x^4 – 3x^3 + 15x^2 + 2x – 1; G(x) = 3x^2\).
b) ![]() \(F(x) = 12x^4 + 10x^3 – x – 3; G(x) = 3x^2 + x + 1\).
\(F(x) = 12x^4 + 10x^3 – x – 3; G(x) = 3x^2 + x + 1\).
Hướng dẫn giải:
a) ![]() \((6x^4 – 3x^3 + 15x^2 + 2x – 1) : 3x^2\)
\((6x^4 – 3x^3 + 15x^2 + 2x – 1) : 3x^2\)
* Cách 1: Phân tích ta thấy (2x – 1) có bậc nhỏ hơn ![]() \(3x^2\) nên (2x – 1) là số dư R(x) của đa thức trên.
\(3x^2\) nên (2x – 1) là số dư R(x) của đa thức trên.
![]() \(= (6x^4 – 3x^3 + 15x^2) : 3x^2\)
\(= (6x^4 – 3x^3 + 15x^2) : 3x^2\)
![]() \(= (6x^4 : 3x^2) + (– 3x^3 : 3x^2) + (15x^2 : 3x^2)\)
\(= (6x^4 : 3x^2) + (– 3x^3 : 3x^2) + (15x^2 : 3x^2)\)
![]() \(= 2x^2 – x + 5\)
\(= 2x^2 – x + 5\)
* Cách 2: Đặt tính:
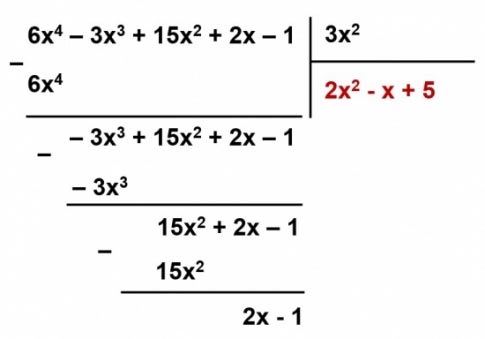
* Vậy: R(x) = 2x – 1
![]() \(Q(x) = 2x^2 – x + 5\)
\(Q(x) = 2x^2 – x + 5\)
![]() \(F(x) = 3x^2 . (2x^2 – x + 5) + 2x – 1\)
\(F(x) = 3x^2 . (2x^2 – x + 5) + 2x – 1\)
b) ![]() \((12x^4 + 10x^3 – x – 3) : (3x^2 + x + 1)\).
\((12x^4 + 10x^3 – x – 3) : (3x^2 + x + 1)\).
Đặt tính:
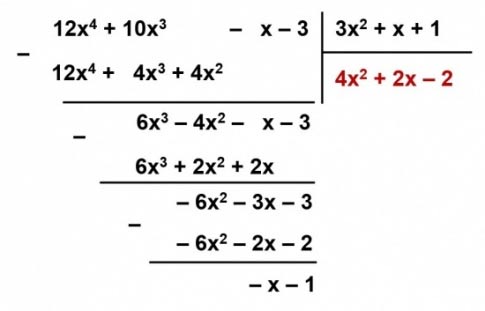
Vậy: R(x) = - x - 1
![]() \(Q(x) = 4x^2 + 2x - 2\)
\(Q(x) = 4x^2 + 2x - 2\)
![]() \(F(x) = (3x^2 + x + 1) . (4x^2 + 2x - 2) - x - 1\)
\(F(x) = (3x^2 + x + 1) . (4x^2 + 2x - 2) - x - 1\)
Bài 7.35 trang 43 SGK Toán 7 tập 2 KNTT
Bạn Tâm lúng túng khi muốn tìm thương và dư trong phép chia đa thức 21x – 4 cho ![]() \(3x^2\). Em có thể giúp bạn Tâm được không?
\(3x^2\). Em có thể giúp bạn Tâm được không?
Hướng dẫn giải:
Phân tích ta thấy (21x – 4) có bậc nhỏ hơn ![]() \(3x^2\) nên (21x – 4) của đa phép chia đa thức 21x – 4 cho
\(3x^2\) nên (21x – 4) của đa phép chia đa thức 21x – 4 cho ![]() \(3x^2\).
\(3x^2\).
* Vậy: Phép chia đa thức 21x – 4 cho ![]() \(3x^2\) có:
\(3x^2\) có:
- Thương là 0.
- Số dư là (21x – 4).







