Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
VnDoc.com Lớp 7 Toán 7 Kết nối - Tập 2

Toán 7 Bài 22: Đại lượng tỉ lệ thuận

Giải Toán 7 Kết nối tri thức
13 3.195
Bài viết đã được lưu

Giải Toán 7 Kết nối tri thức trang 11, 12, 13, 14 tập 2

Mời các bạn tham khảo Giải Toán 7 Bài 22: Đại lượng tỉ lệ thuận sách Kết nối tri thức bao gồm lời giải và đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 2 chương trình sách mới. Lời giải Toán 7 được trình bày chi tiết, dễ hiểu, giúp các em học sinh ôn tập, củng cố kiến thức được học trong bài 22 Toán 7 KNTT. Sau đây mời các bạn tham khảo chi tiết.

Mở đầu trang 11 Toán 7 Tập 2:

Bột sắn dây được làm từ củ sắn dây, là một loại thực phẩm có nhiều tác dụng tốt với sức khỏe. Ông An nhận thấy cứ 4,5 kg củ sắn dây tươi thì thu được khoảng 1 kg bột. Hỏi với 3 tạ củ sắn dây tươi, ông An sẽ thu được khoảng bao nhiêu kilôgam bột sắn dây?

Hướng dẫn giải

Đổi 3 tạ = 300 kg.

Ông An thu được số kilôgam bột sắn dây là:

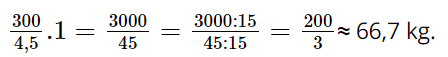
Vậy với 3 tạ củ sắn dây tươi, ông An thu được khoảng 66,7 kg bột sắn dây.

Hoạt động 1 trang 11 SGK Toán 7 Tập 2 KNTT

Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h)

Thay mỗi dấu “?” trong bảng sau bằng số thích hợp:

t (h)

1

1,5

2

3

s (km)

?

?

?

?

Hướng dẫn giải:

Ta đã biết quãng đường vật đi được bằng thời gian vật di chuyển nhân với vận tốc.

Do đó với t = 1 thì s = 60.1 = 60 km.

Với t = 1,5 thì s = 60.1,5 = 90 km.

Với t = 2 thì s = 60.2 = 120 km.

Với t = 3 thì s = 60.3 = 180 km.

Ta có bảng sau:

t (h)

1

1,5

2

3

s (km)

60

90

120

180

Hoạt động 2 trang 11 SGK Toán 7 Tập 2 KNTT

Một xe ô tô di chuyển với vận tốc không đổi 60 km/h. Gọi s (km) là quãng đường ô tô đi được trong khoảng thời gian t (h)

Viết công thức tính quãng đường s theo thời gian di chuyển tương ứng t.

Hướng dẫn giải:

Công thức tính quãng đường s theo thời gian di chuyển tương ứng t là:

s = 60t.

Câu hỏi trang 11 SGK Toán 7 Tập 2 KNTT

Trong HĐ2, quãng đường a tỉ lệ thuận với thời gian t không? Thời gian t có tỉ lệ thuận với quãng đường s không?

Hướng dẫn giải:

Kết quả hoạt động 2: s = 60t

=> Quãng đường s tỉ lệ thuận với thời gian t.

s = 60t => \frac{s}{{60}} = \frac{1}{{60}}.s

=> Thời gian t tỉ lệ thuận với quãng đường s.

Luyện tập 1 trang 12 SGK Toán 7 Tập 2 KNTT

Theo Viện Dinh dưỡng Quốc gia, cứ trong 100 g đậu tương (đậu nành) thì có 34 g protein. Khối lượng protein trong đậu tương có tỉ lệ thuận với khối lượng đậu tương không? Nếu có thì hệ số tỉ lệ là bao nhiêu?

Hướng dẫn giải:

Ta có:

Cứ trong 100 g đậu tương thì có 34 g protein

=> Khối lượng protein trong đậu tương tỉ lệ thuận với khối lượng đậu tương

=> Hệ số tỉ lệ bằng: 34:100 = \frac{{34}}{{100}} = \frac{{17}}{{50}}

Vận dụng trang 12 SGK Toán 7 Tập 2 KNTT

Em hãy giải bài toán mở đầu:

Bột sắn dây được làm từ củ sắn dây, là một loại thực phẩm có nhiều tác dụng tốt với sức khỏe. Ông An nhận thấy cứ 4,5 kg củ sắn dây tươi thì thu được khoảng 1 kg bột. Hỏi với 3 tạ củ sắn dây tươi, ông An sẽ thu được khoảng bao nhiêu kilôgam bột sắn dây?

Hướng dẫn giải:

Đổi 3 tạ = 300 kg

Gọi số kilôgam bột sắn dây ông An thu hoạch được từ 3 tạ củ là x (kg)

Điều kiện: x > 0

Theo bài ra ta có:

Số kilôgam củ sắn dây tươi và số kilôgam bột sắn dây thu được là hai đại lượng tỉ lệ thuận

=> 4,5. x = 300 . 1

=> 4,5x = 300

=> x = \frac{{300}}{{4,5}} \approx 66,7\left( {tm} \right)

Vậy với 3 tạ củ sắn dây tươi, ông An thu được khoảng 66,7 kg bột sắn dây.

Luyện tập 2 trang 13 SGK Toán 7 Tập 2 KNTT

Hai thanh kim loại đồng chất có thể tích tương ứng là 10 cm 3 và 15 cm 3 . Hỏi mỗi thanh nặng bao nhiêu gam, biết rằng một thanh nặng hơn thanh kia 40 g?

Hướng dẫn giải:

Kiến thức quan trọng: Khối lượng của một vật đồng chất tỉ lệ thuận với thể tích của nó.

Gọi khối lượng thanh kim loại có thể tích 10cm3 là x (g)

Khối lượng thanh kim loại có thể tích15 cm3 là: y (g)

Điều kiện: x > 0, y > 0

Do 10 < 15 => x < y

Ta có: Một thanh nặng hơn thanh kia 40 g

=> y – x = 40

Mặt khác khối lượng của một vật tỉ lệ thuận với thể tích của nó

=> \frac{x}{{10}} = \frac{y}{{15}}

Áp dụng tính chất của dãy tỉ số bằng nhau

=> \frac{x}{{10}} = \frac{y}{{15}} = \frac{{y - x}}{{15 - 10}} = \frac{{40}}{5} = 8

=> x = 8 . 10 = 80 (thỏa mãn)

=> y = 8 . 15 = 120 (thỏa mãn)

(hoặc y = x + 40 = 80 + 40 = 120 (g)

Vậy khối lượng thanh kim loại có thể tích 10cm3 là 80g

Khối lượng thanh kim loại có thể tích15 cm3 là 120g

Luyện tập 3 trang 14 SGK Toán 7 Tập 2 KNTT

Hãy chia 1 tấn gạo thành ba phần có khối lượng tỉ lệ thuận với 2; 3; 5

Hướng dẫn giải

Đổi: 1 tấn = 1000kg

Gọi số gạo của ba phần chia lần lượt là x, y, z (kg)

Điều kiện: x > 0, y > 0, z > 0

Theo bài ra ta có:

Tổng số gạo là 1000 kg => x + y + z = 1000

Chia số lượng gạo thành ba phần có khối lượng tỉ lệ thuận với 2; 3; 5

=> \frac{x}{2} = \frac{y}{3} = \frac{z}{5}

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\frac{x}{2} = \frac{y}{3} = \frac{z}{5} = \frac{{x + y + z}}{{2 + 3 + 5}} = \frac{{1000}}{{10}} = 100

=> x = 100 . 2 = 200 (thỏa mãn)

=> y = 100 . 3 = 300 (thỏa mãn)

=> z = 5 . 100 = 500 (thỏa mãn)

Vậy số gạo của ba phần chia lần lượt là 200kg, 300kg, 500kg

Bài 6.17 trang 14 SGK Toán 7 Tập 2 KNTT

Cho biết x, y là hai đại lượng tỉ lệ thuận. Thay mỗi dấu “?” trong bảng sau bằng số thích hợp.

x

2

4

5

?

?

?

y

-6

?

?

9

18

1,5

Viết công thức mô tả mối quan hệ phụ thuộc giữa hai đại lượng x và y.

Hướng dẫn giải:

x

2

4

5

-3

-6

-0,5

y

-6

-12

-15

9

18

1,5

Vì x và y là hai đại lượng tỉ lệ thuận, có \dfrac{{{y_1}}}{{{x_1}}} = \dfrac{{ - 6}}{2} = - 3 nên ta có công thức y = -3. x

Bài 6.18 trang 14 SGK Toán 7 Tập 2 KNTT

Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ thuận không?

Bài 6.18

Hướng dẫn giải:

a) Ta có: \dfrac{5}{{15}} = \dfrac{9}{{27}} = \dfrac{{15}}{{45}} = \dfrac{{24}}{{72}}

nên 2 đại lượng x, y là hai đại lượng tỉ lệ thuận.

b) Ta có: \dfrac{4}{8} = \dfrac{8}{{16}} = \dfrac{{25}}{{50}} \ne \dfrac{{16}}{{30}} nên 2 đại lượng x, y không là hai đại lượng tỉ lệ thuận. \dfrac{5}{{15}} = \dfrac{9}{{27}} = \dfrac{{15}}{{45}} = \dfrac{{24}}{{72}}

Bài 6.19 trang 14 SGK Toán 7 Tập 2 KNTT

Cho biết y tỉ lệ thuận với x theo hệ số tỉ lệ a, x tỉ lệ thuận với z theo hệ số tỉ lệ b. Hỏi y có tỉ lệ thuận với z không? Nếu có thì hệ số tỉ lệ là bao nhiêu?

Hướng dẫn giải:

Vì y tỉ lệ thuận với x theo hệ số tỉ lệ a nên y = a.x

Vì x tỉ lệ thuận với z theo hệ số tỉ lệ b nên x = b.z

Do đó, y = a.x = a.(b.z ) = (a.b).z ( a,b là hằng số vì a,b là các hằng số)

Vậy y có tỉ lệ thuận với z và hệ số tỉ lệ là a.b

Bài 6.20 trang 14 SGK Toán 7 Tập 2 KNTT

Hai bể nước hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau, nhưng chiều cao của bể thứ nhất bằng \dfrac{3}{4} chiều cao của bể thứ hai. Để bơm đầy nước vào bể thứ nhất mất 4,5 giờ. Hỏi phải mất bao nhiêu thời gian để bơm đầy nước vào bể thứ hai (nếu dùng máy bơm có cùng công suất)?

Hướng dẫn giải:

Gọi thời gian để bơm đầy nước vào bể thứ hai là x (giờ) (x > 0)

Vì 2 bể nước hình hộp chữ nhật có chiều dài và chiều rộng tương ứng bằng nhau và máy bơm có cùng công suất nên chiều cao bể nước và thời gian đầy bể là hai đại lượng tỉ lệ thuận.

Áp dụng tính chất của hai đại lượng tỉ lệ thuận, ta có:

\dfrac{3}{4} = \dfrac{{4,5}}{x} \Rightarrow x = \dfrac{{4.4,5}}{3} = 6(thỏa mãn)

Vậy thời gian để bơm đầy nước vào bể thứ hai là 6 giờ

Bài 6.21 trang 14 SGK Toán 7 Tập 2 KNTT

Để chuẩn bị cho học sinh làm thí nghiệm, cô Hương chia 1,5 lít hóa chất thành ba phần tỉ lệ thuận với 4;5;6 và đựng trong ba chiếc lọ. Hỏi mỗi chiếc lọ đựng bao nhiêu lít hóa chất đó?

Hướng dẫn giải:

Gọi thể tích 3 phần lần lượt là x,y,z (lít) (x,y,z > 0)

Vì cô Hương chia 1,5 lít hóa chất thành ba phần nên x+y+z=1,5

Vì ba phần tỉ lệ thuận với 4;5;6 nên \dfrac{x}{4} = \dfrac{y}{5} = \dfrac{z}{6}

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\begin{array}{l}\dfrac{x}{4} = \dfrac{y}{5} = \dfrac{z}{6} = \dfrac{{x + y + z}}{{4 + 5 + 6}} = \dfrac{{1,5}}{{15}} = 0,1\\ \Rightarrow x = 0,1.4 = 0,4\\y = 0,1.5 = 0,5\\z = 0,1.6 = 0,6\end{array}

Vậy 3 chiếc lọ đựng lần lượt là 0,4 lít, 0,5 lít, 0,6 lít hóa chất.

.....................

Ngoài Giải Toán 7 Bài 2: Đại lượng tỉ lệ thuận, mời các bạn tham khảo thêm tài liệu học tập lớp 7 khác như Ngữ văn 7 , Toán 7 và các Đề thi học kì 1 lớp 7 , Đề thi học kì 2 lớp 7 ... được cập nhật liên tục trên VnDoc.com.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau đây:

Nhóm Tài liệu học tập lớp 7

Nhóm Sách Kết nối tri thức THCS

Bài tiếp theo: Giải Toán 7 Bài 23: Đại lượng tỉ lệ nghịch

Đánh giá bài viết
13 3.195
Tìm thêm: giải sgk toán 7 giải bài tập toán 7 soạn toán 7
Sắp xếp theo
Xóa Đăng nhập để Gửi
     

    Tham khảo thêm

    Toán 7 Kết nối - Tập 2

    Xem thêm