Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên

Giải Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên được biên soạn nhằm đồng hành cùng các em học sinh trong quá trình chinh phục chương trình SGK Kết nối tri thức với cuộc sống (Tập 2). Với hệ thống lời giải chi tiết và phương pháp giải tối ưu cho các bài tập trang 64, 65, nội dung này không chỉ giúp các em hoàn thiện bài tập về nhà mà còn là công cụ hữu hiệu để ôn tập, củng cố lý thuyết và rèn luyện tư duy hình học sắc bén. Hy vọng đây sẽ là nguồn tham khảo giá trị giúp các em tự tin hơn trong môn Toán lớp 7. Mời các em cùng theo dõi chi tiết nội dung dưới đây.

Hoạt động trang 64 SGK Toán 7 tập 2 KNTT

Cho điểm A không nằm trên đường thẳng d.

a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.

b) Em hãy giải thích vì sao AH < AM.

Hướng dẫn giải

a) Hình vẽ minh họa

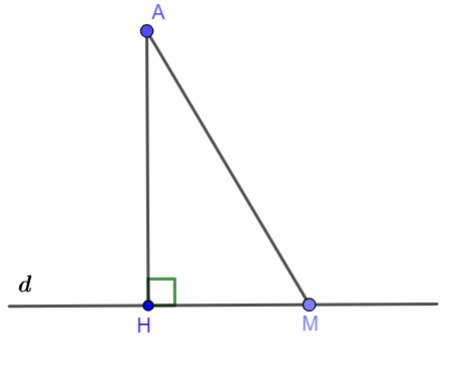
b) Ta có: AH ⊥ d =>

=> là góc lớn nhất trong ∆AHM

=> Cạnh AM là cạnh lớn nhất trong ∆AHM.

=> AH < AM

Luyện tập trang 64 SGK Toán 7 tập 2 KNTT

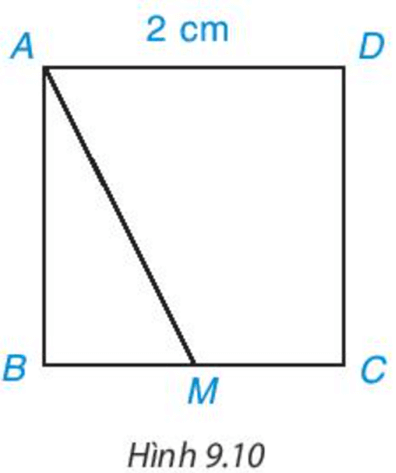
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.

a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.

b) So sánh hai đoạn thẳng AB và AM.

c) Tìm khoảng cách từ điểm C đến đường thẳng AB.

Hướng dẫn giải

a) Đường vuông góc kẻ từ A đến đường thẳng BC là AB.

Đường xiên kẻ từ A đến đường thẳng BC là AM.

b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AM > AB.

c) Khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn BC.

Do ABCD là hình vuông nên BC = AD = 2 cm.

Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.

Vận dụng trang 64 Toán lớp 7 Tập 2:

Em hãy trả lời câu hỏi trong tình huống mở đầu.

Hướng dẫn giải

Ta có OA là đường vuông góc kẻ từ O đến AC.

OB và OC là các đường xiên kẻ từ O đến AC nên OB > OA và OC > OA.

Do đó để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.

Thử thách trang 64 Toán lớp 7 Tập 2:

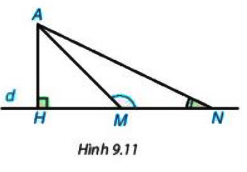
a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.

b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?

Hướng dẫn giải

a) Với HM < HN ta có:

(Do là góc ngoài tại đỉnh M của ∆AHM)

=> là góc tù

=> là góc lớn nhất trong ∆AMN

=> Cạnh AN là cạnh lớn nhất trong ∆AMN

=> AM < AN

b)

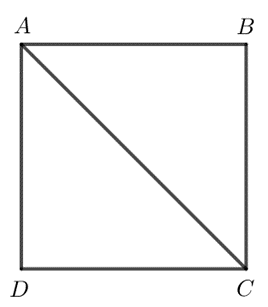
Nếu M nằm trên AB hoặc AD thì AM ≤ AB (*)

Nếu M nằm trên BC hoặc CD thì AM ≤ AC (**)

Ta lại có:

AB là đường vuông góc kẻ từ A đến BC

AC là đường xiên kẻ từ A đến BC

=> AC > AB

Từ (*) và (**) => Giá trị của đoạn AM lớn nhất bằng đoạn AC

Điều đó xảy ra khi điểm M trùng với điểm C

Vậy AM lớn nhất khi M trùng C

Bài 9.6 trang 65 SGK Toán 7 tập 2 KNTT

Chiều cao của tam giác ứng với một cạnh của nó có phải khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?

Hướng dẫn giải:

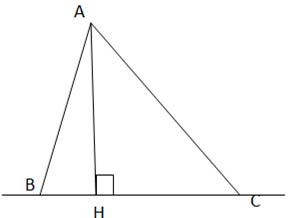
Dựa theo hình thì AH chính là chiều cao của tam giác ABC. AH ⊥ BC và AH là đoạn ngắn nhất so với AB và AC nên AH chính là khoảng cách từ a đến đoạn thẳng BC.

Bài 9.7 trang 65 SGK Toán 7 tập 2 KNTT

Cho hình vuông ABCD. Hỏi trong 4 đỉnh của hình vuông

a) Đỉnh nào cách đều hai điểm A và C

b) Đỉnh nào cách đều hai đường thẳng AB và AD

Hướng dẫn giải:

a) Đỉnh B và đỉnh D

b) Đỉnh C

Bài 9.8 trang 65 SGK Toán 7 tập 2 KNTT

Cho tam giác cân ABc, AB=AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12)

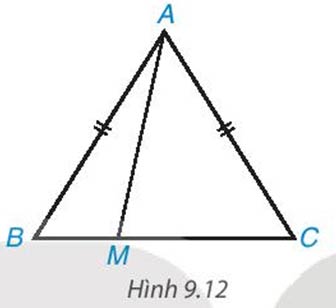
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M đê độ dài AM nhỏ nhất

b) Chứng minh răng với mọi điểm M thì AM<AB

Hướng dẫn giải:

a)

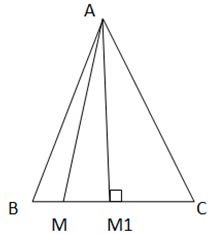
Gọi M1 là trung điểm của cạnh đáy BC. Suy ra AM1 ⊥ BC. AM1 chính là khoảng cách từ A đến BC

Theo định lí về đường xiên và đường vuông góc thì AM1 chính là đường ngắn nhất trong tam giác ABC

Vậy nếu M là trung điểm của BC thì AM sẽ có độ dài nhỏ nhất

b) Khi M nằm giữa C và B

Nếu BM < MC thì ta sẽ được góc tù . Theo định lý về góc và cạnh đối diện, AB sẽ lớn hơn AM

Tương tự khi BM>MC. ta sẽ được góc tù . Theo định lý về góc và cạnh đối diện, AC sẽ lớn hơn AM

Mà AB=AC. Suy ra, bất cứ điểm nào nằm giữa B và C, AM luôn bé hơn AB.

Bài 9.9 trang 65 SGK Toán 7 tập 2 KNTT

Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC ( M,N không phải là đỉnh của tam giác). (H.9.13). Chứng minh rằng MN < BC. Gợi ý, so sánh MN với NB, NB với BC).

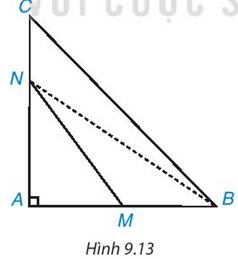
Hướng dẫn giải: