Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác

Giải Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác sách Kết nối tri thức bao gồm lời giải và đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 2 chương trình sách mới. Lời giải Toán 7 được trình bày chi tiết, dễ hiểu, giúp các em học sinh ôn tập, củng cố kiến thức được học, từ đó luyện giải Toán 7 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.

Mở đầu trang 72 SGK Toán 7 tập 2 KNTT

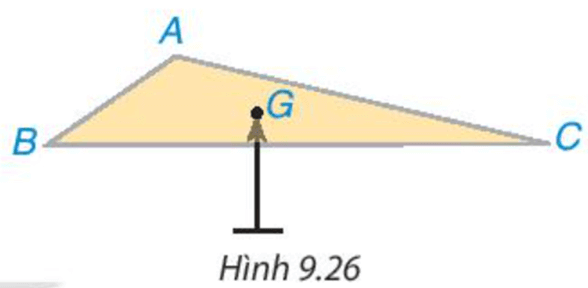
Hình 9.26 mô phỏng một miếng bìa hình tam giác ABC đặt thăng bằng trên giá nhọn tại điểm G. Điểm đó được xác định như thế nào và có gì đặc biệt?

Hướng dẫn giải:

Điểm G là giao điểm ba đường trung tuyến của ∆ABC và G là trọng tâm của ∆ABC .

Câu hỏi trang 72 SGK Toán 7 tập 2 KNTT

Mỗi tam giác có mấy đường trung tuyến?

Hướng dẫn giải:

Mỗi tam giác có ba đường trung tuyến xuất phát từ ba đỉnh của tam giác tới trung điểm của cạnh đối diện.

HĐ1 trang 72 SGK Toán 7 tập 2 KNTT

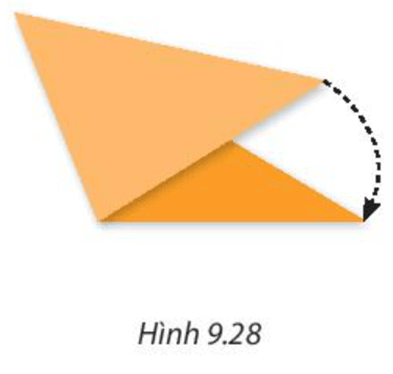
Hãy lấy một mảnh giấy hình tam giác, gấp giấy đánh dấu trung điểm của các cạnh. Sau đó, gấp giấy để được các nếp gấp đi quả đỉnh và trung điểm của cạnh đối diện (tức là các đường trung tuyến của tam giác). Mở tờ giấy ra, quan sát và cho biết ba nếp gấp (ba đường trung tuyến) có cùng đi qua một điểm không (H.9.28)

Hướng dẫn giải:

Học sinh tự thực hiện gấp giấy.

Ba nếp gấp (ba đường trung tuyến) cùng đi qua một điểm.

HĐ2 trang 73 SGK Toán 7 tập 2 KNTT

Trên mảnh giấy kẻ ô vuông, mỗi chiều 10 ô, hãy đếm dòng, đánh dấu các đỉnh A, B, C rồi vẽ tam giác ABC (H.9.29).

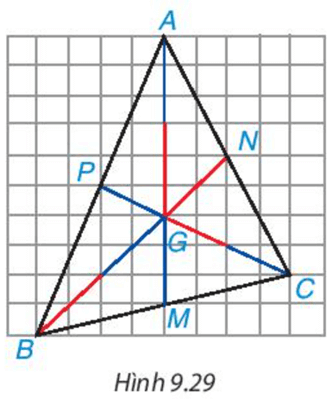
Vẽ hai đường trung tuyến BN, CP, chúng cắt nhau tại G; tia AG cắt BC tại M.

- AM có phải là đường trung tuyến của tam giác ABC không?

- Hãy xác định các tỉ số

Hướng dẫn giải:

- Ta có: MB = MC và M nằm giữa B và C nên M là trung điểm của BC.

Do đó, AM có là đường trung tuyến của tam giác ABC

- Ta có:

Luyện tập 1 trang 73 SGK Toán 7 tập 2 KNTT

Trong tam giác ABC ở Ví dụ 1, với AM là đường trung tuyến và G là trọng tâm của tam giác. Cho trung tuyến BN và GN = 1 cm. Tính GB và NB.

Hướng dẫn giải:

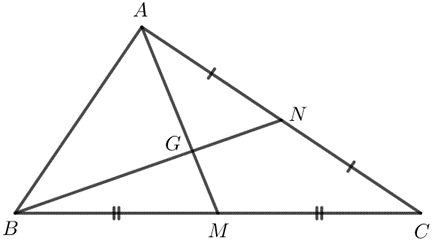
Vì G là trọng tâm của tam giác ABC nên

Ta có: GN = NB – GB = NB - =

Mà GN = 1 cm nên 1 = ( cm)

GB = = = 2 ( cm)

Vậy GB = 2 cm, NB = 3 cm.

Tranh luận trang 74 SGK Toán 7 tập 2 KNTT

Vuông: “Tớ tìm trọng tâm của một tam giác bằng cách lấy giao điểm của hai đường trung tuyến”.

Tròn: “Tớ còn cách khác nữa cơ”.

Anh Pi: “Các em có những cách nào?”

Hướng dẫn giải:

Các cách để tìm trọng tâm của tam giác:

Cách 1. Lấy giao điểm của hai đường trung tuyến của tam giác.

Cách 2. Trên một đường trung tuyến của tam giác, chọn một điểm sao cho khoảng cách từ điểm đó đến đỉnh bằng độ dài đường trung tuyến đó.

Vận dụng 1 trang 74 SGK Toán 7 tập 2 KNTT

Trong tình huống mở đầu, người ta chứng minh được G chính là trọng tâm của tam giác ABC. Em hãy cắt một mảnh bìa hình tam giác. Xác định trọng tâm của tam giác và đặt mảnh bìa đó lên một giá nhọn tại trọng tâm vừa xác định. Quan sát xem mảnh bìa có thăng bằng không.

Hướng dẫn giải:

Học sinh tự thực hiện việc cắt và đặt mảnh bìa.

Sau khi đặt mảnh bìa, ta thấy mảnh bìa có thăng bằng.

HĐ3 trang 74 SGK Toán 7 tập 2 KNTT

Cắt một tam giác bằng giấy. Hãy gấp tam giác vừa cắt để được ba đường phân giác của nó. Mở tờ giấy ra, hãy quan sát và cho biết ba nếp gấp đó có cùng đi qua một điểm không (H.9.33).

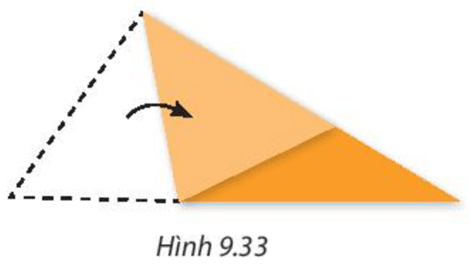
Hướng dẫn giải:

Học sinh thực hiện theo hướng dẫn.

Ba nếp gấp đo cùng đi qua một điểm.

Vận dụng 2 trang 75 Toán 7 Tập 2:

Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Hướng dẫn giải:

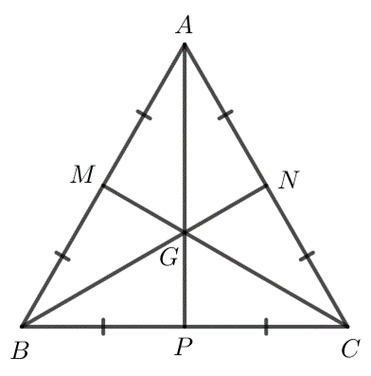
Vì đều nên AB = AC = BC (tính chất tam giác đều)

Vì I là điểm cách đều 3 cạnh của tam giác nên là giao điểm của 3 đường phân giác của tam giác ABC

Áp dụng ví dụ 2, ta được, AI là đường trung tuyến của

Tương tự, ta cũng được BI, CI là đường trung tuyến của

Vậy I là giao điểm của ba đường đường trung tuyến của nên I là trọng tâm của

Chú ý:

Với tam giác đều, giao điểm của 3 đường trung tuyến cũng là giao điểm của 3 đường phân giác.

Bài 9.20 trang 76 SGK Toán 7 tập 2 KNTT

Cho tam giác ABC với hai đường trung tuyến BN,CP và trọng tâm G. Hãy tìm số thích hợp đặt vào dấu ''?'' để được các đẳng thức:

BG = ? BN, CG = ? CP; BG = ? GN, CG = ? GP

Hướng dẫn giải:

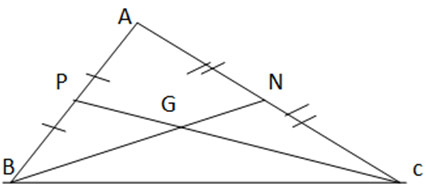
G là trọng tâm của tam giác ABC

Tương tự:

Bài 9.21 trang 76 SGK Toán 7 tập 2 KNTT

Chứng minh rằng

a) Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên là hai đoạn thẳng bằng nhau

b) Ngược lại nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân

Hướng dẫn giải:

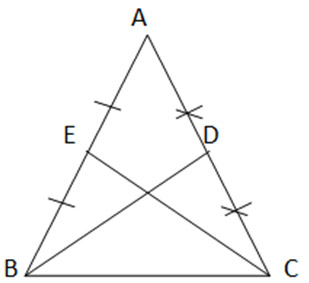
a) Ta có ∆ ABC cân tại A. BD và CE là trung tuyến với E là trung điểm của AB, D là trung điểm của AC

∆ ABC cân tại A => AB = AC

Có:

=> AE= AD

Xét ∆ ABD và ∆ ACE ta có:

chung

AE=AD

AB= AC

=> ∆ ABD = ∆ ACE => BD= CE

b)

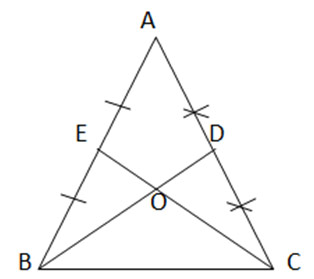
Gọi O là giao điểm của CE và BD

Ta có CE và BD là 2 đường trung tuyến nên O sẽ là trọng tâm của tam giác ∆ ABC

CE= BD

=> BO= CO. OD= OE

Xét ∆ EOB và ∆ DOC ta có:

BO= OC

OD= OE

(2 góc đối đỉnh)

=> ∆ EOB = ∆ DOC

=> EB= DC

Có

=> AB= AC

=> ∆ ABC cân tại A

Bài 9.22 trang 76 SGK Toán 7 tập 2 KNTT

Cho tam giác ABC có các đường trung tuyến BM và CN cắt nhau tại G. Biết góc GBC lớn hơn góc GCB. Hãy so sánh BM và CN.

Hướng dẫn giải:

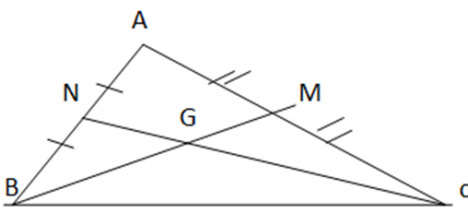
BM, CN là 2 đường trung tuyến cắt nhau tại

=> G là trọng tâm của tám giác ABC

(1)

Xét theo định lí quan hệ giữa góc và cạnh tỏng tam giác ta có

Trong tam giác GBC:

=> CG > GB (2)

Từ (1) và (2) => CN > BM

Bài 9.23 trang 76 SGK Toán 7 tập 2 KNTT

Kí hiệu I là điểm đồng quy của ba đường phân giác trong tam giác ABC. Tính góc BIC khi biết góc BAC = 120°

Hướng dẫn giải:

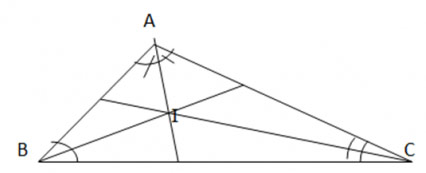
Có I là điểm đồng quy của ba đường phân giác trong tam giác ABC

=> AI, BI, CI lần lượt là đường phân giác của 3 góc

Ta có:

Xét trong tam giác IBC ta có:

Bài 9.24 trang 76 SGK Toán 7 tập 2 KNTT

Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chúng minh BE= CF

Hướng dẫn giải:

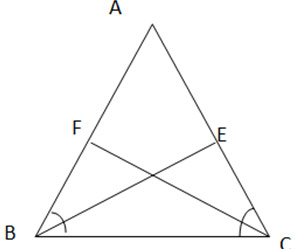
∆ABC cân tại A

BE là đường phân giác của

CF là đường phân giác của

Từ (1), (2), (3)

Xét ∆ ABE và ∆ ACF, ta có:

chung

AB= AC

=> ∆ ABE = ∆ ACF

=> BE = CF

Bài 9.25 trang 76 SGK Toán 7 tập 2 KNTT

Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB

a) Hãy giải thích tại sao DP = DR

b) Hãy giải thích tại sao DP = DQ

c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A

Hướng dẫn giải:

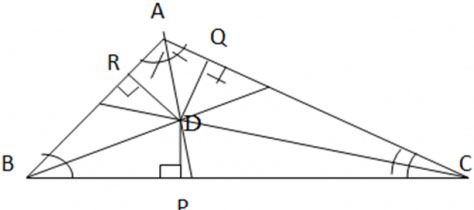
a) Ta có ∆ BPD và ∆ BRD đều là tam giác vuông tại và

Xét 2 tam giác vuông là ∆BRD và ∆BPD ta có:

Chung cạnh BD

(BD là phân giác của hay )

=> ∆BRD = ∆BPD

=> DR=DP

b) Ta có ∆ CPD và ∆ CQD đều là tam giác vuông tại và

Xét 2 tam giác vuông là ∆CPD và ∆CQD ta có:

Chung cạnh CD

(CD là phân giác của hay )

=> ∆ CPD = ∆CQD

=> DP = DQ

c) Từ a và b ta có DR = DQ

Xét 2 tam giác vuông là ∆ARD và ∆AQD ta có:

Chung cạnh AD

DR = DQ

=> ∆ ARD = ∆AQD

=> D nằm trên đường phân giác của

.....................

Trên đây VnDoc đã gửi tới các bạn tài liệu Giải Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác. Ngoài tài liệu trên, mời các bạn tham khảo thêm tài liệu học tập lớp 7 khác như Ngữ văn 7 , Toán 7 và các Đề thi học kì 1 lớp 7 , Đề thi học kì 2 lớp 7 ... được cập nhật liên tục trên VnDoc.com.

Bài tiếp theo: Giải Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác.