VnDoc.com

Toán 7 Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc

Giải Toán 7 Cánh diều

Bài trước

Tải về

Bài sau

Lớp: Lớp 7

Môn: Toán

Dạng tài liệu: Giải bài tập

Bộ sách: Cánh diều

Loại File: PDF

Phân loại: Tài liệu Tính phí

Giải Toán 7 Cánh diều Bài 4: Thứ tự thực hiện các phép tính. Quy tắc dấu ngoặc hướng dẫn giải bài tập trong SGK Toán 7 Cánh diều tập 1 trang 23, 24, 25, 26, giúp các em nắm vững kiến thức được học trong bài và luyện giải bài tập môn Toán lớp 7. Mời các bạn tham khảo chi tiết.

Giải Toán 7 tập 1 trang 25, 26 Cánh diều

I. Thứ tự thực hiện các phép tính
- Luyện tập 1 trang 23 Toán lớp 7 Tập 1:
- Luyện tập 2 trang 24 Toán lớp 7 Tập 1:
II. Quy tắc dấu ngoặc
- Luyện tập 3 trang 25 Toán lớp 7 Tập 1:
- Luyện tập 4 trang 25 Toán lớp 7 Tập 1:
Giải bài tập trang 25 Toán 7 tập 1 Cánh diều

I. Thứ tự thực hiện các phép tính

Luyện tập 1 trang 23 Toán lớp 7 Tập 1:

Tính giá trị của mỗi biểu thức sau:

a) $0,2 + 2,5:\frac{7}{2}$ $0,2 + 2,5:\frac{7}{2}$

b) $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$ $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$

Hướng dẫn giải:

a) $0,2 + 2,5:\frac{7}{2}$ $0,2 + 2,5:\frac{7}{2}$

$\begin{matrix} = \dfrac{2}{{10}} + \dfrac{5}{2}:\dfrac{7}{2} = \dfrac{1}{5} + \dfrac{5}{2}.\dfrac{2}{7} \hfill \\ = \dfrac{1}{5} + \dfrac{5}{7} = \dfrac{7}{{35}} + \dfrac{{25}}{{35}} = \dfrac{{32}}{{35}} \hfill \\ \end{matrix}$ $\begin{matrix} = \dfrac{2}{{10}} + \dfrac{5}{2}:\dfrac{7}{2} = \dfrac{1}{5} + \dfrac{5}{2}.\dfrac{2}{7} \hfill \\ = \dfrac{1}{5} + \dfrac{5}{7} = \dfrac{7}{{35}} + \dfrac{{25}}{{35}} = \dfrac{{32}}{{35}} \hfill \\ \end{matrix}$

b) $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$ $9.{\left( { - \frac{1}{3}} \right)^2} - {\left( { - 0,1} \right)^3}:\frac{2}{{15}}$

$\begin{matrix} = 9.\dfrac{1}{9} - {\left( { - \dfrac{1}{{10}}} \right)^3}:\dfrac{2}{{15}} \hfill \\ = 1 - \left( { - \dfrac{1}{{1000}}} \right):\dfrac{2}{{15}} \hfill \\ = 1 + \dfrac{1}{{1000}}:\dfrac{2}{{15}} = 1 + \dfrac{1}{{1000}}.\dfrac{{15}}{2} = 1 + \dfrac{3}{{400}} = \dfrac{{403}}{{400}} \hfill \\ \end{matrix}$ $\begin{matrix} = 9.\dfrac{1}{9} - {\left( { - \dfrac{1}{{10}}} \right)^3}:\dfrac{2}{{15}} \hfill \\ = 1 - \left( { - \dfrac{1}{{1000}}} \right):\dfrac{2}{{15}} \hfill \\ = 1 + \dfrac{1}{{1000}}:\dfrac{2}{{15}} = 1 + \dfrac{1}{{1000}}.\dfrac{{15}}{2} = 1 + \dfrac{3}{{400}} = \dfrac{{403}}{{400}} \hfill \\ \end{matrix}$

Luyện tập 2 trang 24 Toán lớp 7 Tập 1:

Tính giá trị của mỗi biểu thức sau:

a) $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$ $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$

b) $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$ $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$

Hướng dẫn giải:

a) $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$ $\left( {0,25 - \frac{5}{6}} \right).1,6 + \frac{{ - 1}}{3}$

$\begin{matrix} = \left( {\dfrac{{25}}{{100}} - \dfrac{5}{6}} \right).\dfrac{{16}}{{10}} + \dfrac{{ - 1}}{3} \hfill \\ = \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right).\dfrac{8}{5} + \dfrac{{ - 1}}{3} \hfill \\ = \dfrac{2}{5} - \dfrac{4}{3} + \dfrac{{ - 1}}{3} = \dfrac{2}{5} + \left( { - \dfrac{4}{3} + \dfrac{{ - 1}}{3}} \right) \hfill \\ = \dfrac{2}{5} + \left( {\dfrac{{ - 5}}{3}} \right) = \dfrac{6}{{15}} - \dfrac{{25}}{{15}} = \dfrac{{ - 19}}{{15}} \hfill \\ \end{matrix}$ $\begin{matrix} = \left( {\dfrac{{25}}{{100}} - \dfrac{5}{6}} \right).\dfrac{{16}}{{10}} + \dfrac{{ - 1}}{3} \hfill \\ = \left( {\dfrac{1}{4} - \dfrac{5}{6}} \right).\dfrac{8}{5} + \dfrac{{ - 1}}{3} \hfill \\ = \dfrac{2}{5} - \dfrac{4}{3} + \dfrac{{ - 1}}{3} = \dfrac{2}{5} + \left( { - \dfrac{4}{3} + \dfrac{{ - 1}}{3}} \right) \hfill \\ = \dfrac{2}{5} + \left( {\dfrac{{ - 5}}{3}} \right) = \dfrac{6}{{15}} - \dfrac{{25}}{{15}} = \dfrac{{ - 19}}{{15}} \hfill \\ \end{matrix}$

b) $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$ $3 - 2.\left[ {0,5 + \left( {0,25 - \frac{1}{6}} \right)} \right]$

$\begin{matrix} = 3 - 2.\left[ {\dfrac{5}{{10}} + \left( {\dfrac{{25}}{{100}} - \dfrac{1}{6}} \right)} \right] \hfill \\ = 3 - 2.\left[ {\dfrac{1}{2} + \left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)} \right] \hfill \\ = 3 - 2.\dfrac{1}{2} - 2.\left( {\dfrac{1}{4} - \dfrac{1}{6}} \right) \hfill \\ = 3 - 1 - 2.\dfrac{1}{4} + 2.\dfrac{1}{6} = 2 - \dfrac{1}{2} + \dfrac{1}{3} \hfill \\ = \dfrac{{12}}{6} - \dfrac{3}{6} + \dfrac{2}{6} = \dfrac{{11}}{6} \hfill \\ \end{matrix}$ $\begin{matrix} = 3 - 2.\left[ {\dfrac{5}{{10}} + \left( {\dfrac{{25}}{{100}} - \dfrac{1}{6}} \right)} \right] \hfill \\ = 3 - 2.\left[ {\dfrac{1}{2} + \left( {\dfrac{1}{4} - \dfrac{1}{6}} \right)} \right] \hfill \\ = 3 - 2.\dfrac{1}{2} - 2.\left( {\dfrac{1}{4} - \dfrac{1}{6}} \right) \hfill \\ = 3 - 1 - 2.\dfrac{1}{4} + 2.\dfrac{1}{6} = 2 - \dfrac{1}{2} + \dfrac{1}{3} \hfill \\ = \dfrac{{12}}{6} - \dfrac{3}{6} + \dfrac{2}{6} = \dfrac{{11}}{6} \hfill \\ \end{matrix}$

II. Quy tắc dấu ngoặc

Luyện tập 3 trang 25 Toán lớp 7 Tập 1:

Tính một cách hợp lí:

a) $1,8 - \left( {\frac{3}{7} - 0,2} \right)$ $1,8 - \left( {\frac{3}{7} - 0,2} \right)$

b)

Hướng dẫn giải:

a) $1,8 - \left( {\frac{3}{7} - 0,2} \right)$ $1,8 - \left( {\frac{3}{7} - 0,2} \right)$

$\begin{matrix} = 1,8 - \dfrac{3}{7} + 0,2 \hfill \\ = \left( {1,8 + 0,2} \right) - \dfrac{3}{7} \hfill \\ = 2 - \dfrac{3}{7} = \dfrac{{14}}{7} - \dfrac{3}{7} = \dfrac{{11}}{7} \hfill \\ \end{matrix}$ $\begin{matrix} = 1,8 - \dfrac{3}{7} + 0,2 \hfill \\ = \left( {1,8 + 0,2} \right) - \dfrac{3}{7} \hfill \\ = 2 - \dfrac{3}{7} = \dfrac{{14}}{7} - \dfrac{3}{7} = \dfrac{{11}}{7} \hfill \\ \end{matrix}$

b) $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$ $12,5 - \frac{{16}}{{13}} + \frac{3}{{13}}$

$\begin{matrix} = 12,5 + \left( { - \dfrac{{16}}{{13}} + \dfrac{3}{{13}}} \right) \hfill \\ = 12,5 + \left( {\dfrac{{ - 13}}{{13}}} \right) \hfill \\ = 12,5 + \left( { - 1} \right) = 12,5 - 1 = 11,5 \hfill \\ \end{matrix}$ $\begin{matrix} = 12,5 + \left( { - \dfrac{{16}}{{13}} + \dfrac{3}{{13}}} \right) \hfill \\ = 12,5 + \left( {\dfrac{{ - 13}}{{13}}} \right) \hfill \\ = 12,5 + \left( { - 1} \right) = 12,5 - 1 = 11,5 \hfill \\ \end{matrix}$

Luyện tập 4 trang 25 Toán lớp 7 Tập 1:

Tính một cách hợp lí:

a) $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$ $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$

b) $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$ $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$

Hướng dẫn giải:

a) $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$ $\left( { - \frac{5}{6}} \right) - \left( { - 1,8} \right) + \left( { - \frac{1}{6}} \right) - 0,8$

$\begin{matrix} = \left[ {\left( { - \dfrac{5}{6}} \right) + \left( { - \dfrac{1}{6}} \right)} \right] + \left[ { - 0,8 - \left( { - 1,8} \right)} \right] \hfill \\ = - \dfrac{6}{6} + \left[ { - 0,8 + 1,8} \right] \hfill \\ = - 1 + 1 = 0 \hfill \\ \end{matrix}$ $\begin{matrix} = \left[ {\left( { - \dfrac{5}{6}} \right) + \left( { - \dfrac{1}{6}} \right)} \right] + \left[ { - 0,8 - \left( { - 1,8} \right)} \right] \hfill \\ = - \dfrac{6}{6} + \left[ { - 0,8 + 1,8} \right] \hfill \\ = - 1 + 1 = 0 \hfill \\ \end{matrix}$

b) $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$ $\left( { - \frac{9}{7}} \right) + \left( { - 1,23} \right) - \left( { - \frac{2}{7}} \right) - 0,77$

$\begin{matrix} = \left[ {\left( { - \dfrac{9}{7}} \right) - \left( { - \dfrac{2}{7}} \right)} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right] \hfill \\ = \left[ {\left( { - \dfrac{9}{7}} \right) + \dfrac{2}{7}} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right] \hfill \\ = - \dfrac{7}{7} + \left( { - 2} \right) = - 1 - 2 = - 3 \hfill \\ \end{matrix}$ $\begin{matrix} = \left[ {\left( { - \dfrac{9}{7}} \right) - \left( { - \dfrac{2}{7}} \right)} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right] \hfill \\ = \left[ {\left( { - \dfrac{9}{7}} \right) + \dfrac{2}{7}} \right] + \left[ {\left( { - 1,23} \right) - 0,77} \right] \hfill \\ = - \dfrac{7}{7} + \left( { - 2} \right) = - 1 - 2 = - 3 \hfill \\ \end{matrix}$

Giải bài tập trang 25 Toán 7 tập 1 Cánh diều

Bài 1 trang 25 Toán 7 tập 1 Cánh diều

Tính

$a) \frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};$ $a) \frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3};$

$b) {\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.$ $b) {\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}.$

Hướng dẫn giải:

a) $\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3}$ $\frac{1}{9} - 0,3.\frac{5}{9} + \frac{1}{3}$

$\begin{matrix} = \dfrac{1}{9} - \dfrac{3}{{10}}.\dfrac{5}{9} + \dfrac{1}{3} \hfill \\ = \dfrac{1}{9} - \dfrac{1}{6} + \dfrac{1}{3} \hfill \\ = \dfrac{2}{{18}} - \dfrac{3}{{18}} + \dfrac{6}{{18}} = \dfrac{5}{{18}} \hfill \\ \end{matrix}$ $\begin{matrix} = \dfrac{1}{9} - \dfrac{3}{{10}}.\dfrac{5}{9} + \dfrac{1}{3} \hfill \\ = \dfrac{1}{9} - \dfrac{1}{6} + \dfrac{1}{3} \hfill \\ = \dfrac{2}{{18}} - \dfrac{3}{{18}} + \dfrac{6}{{18}} = \dfrac{5}{{18}} \hfill \\ \end{matrix}$

b) ${\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}$ ${\left( {\frac{{ - 2}}{3}} \right)^2} + \frac{1}{6} - {\left( { - 0,5} \right)^3}$

$\begin{matrix} = {\left( {\dfrac{{ - 2}}{3}} \right)^2} + \dfrac{1}{6} - {\left( { - \dfrac{1}{2}} \right)^3} = \dfrac{4}{9} + \dfrac{1}{6} - \left( { - \dfrac{1}{8}} \right) \hfill \\ = \dfrac{4}{9} + \dfrac{1}{6} + \dfrac{1}{8} = \dfrac{{32}}{{72}} + \dfrac{{12}}{{72}} + \dfrac{9}{{72}} = \dfrac{{53}}{{72}} \hfill \\ \end{matrix}$ $\begin{matrix} = {\left( {\dfrac{{ - 2}}{3}} \right)^2} + \dfrac{1}{6} - {\left( { - \dfrac{1}{2}} \right)^3} = \dfrac{4}{9} + \dfrac{1}{6} - \left( { - \dfrac{1}{8}} \right) \hfill \\ = \dfrac{4}{9} + \dfrac{1}{6} + \dfrac{1}{8} = \dfrac{{32}}{{72}} + \dfrac{{12}}{{72}} + \dfrac{9}{{72}} = \dfrac{{53}}{{72}} \hfill \\ \end{matrix}$

Bài 2 trang 25 Toán 7 tập 1 Cánh diều

Tính

$a) \left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5$ $a) \left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5$

$b) 1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}$ $b) 1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}$

$c)\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4$ $c)\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4$

$d) 0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}$ $d) 0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}$

Hướng dẫn giải:

a)

$\begin{array}{l}\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\\ = \frac{{ - 1}}{5}.\frac{5}{3} - \frac{2}{3}.\frac{1}{2}\\ = \frac{{ - 1}}{3} - \frac{1}{3}\\ = \frac{{ - 2}}{3}\end{array}$ $\begin{array}{l}\left( {\frac{4}{5} - 1} \right):\frac{3}{5} - \frac{2}{3}.0,5\\ = \frac{{ - 1}}{5}.\frac{5}{3} - \frac{2}{3}.\frac{1}{2}\\ = \frac{{ - 1}}{3} - \frac{1}{3}\\ = \frac{{ - 2}}{3}\end{array}$

b)

$\begin{array}{l}1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{5}{9} - \frac{6}{9}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{{ - 1}}{9}} \right)^2}.\frac{{27}}{4}\\ = 1 - \frac{1}{{81}}.\frac{{27}}{4}\\ = 1 - \frac{1}{{12}}\\ = \frac{{11}}{{12}}\end{array}$ $\begin{array}{l}1 - {\left( {\frac{5}{9} - \frac{2}{3}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{5}{9} - \frac{6}{9}} \right)^2}:\frac{4}{{27}}\\ = 1 - {\left( {\frac{{ - 1}}{9}} \right)^2}.\frac{{27}}{4}\\ = 1 - \frac{1}{{81}}.\frac{{27}}{4}\\ = 1 - \frac{1}{{12}}\\ = \frac{{11}}{{12}}\end{array}$

c)

$\begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array} \begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array}$ $\begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array} \begin{array}{l}\left[ {\left( {\frac{3}{8} - \frac{5}{{12}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\left( {\frac{9}{{24}} - \frac{{10}}{{24}}} \right).6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{{24}}.6 + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 1}}{4} + \frac{1}{3}} \right].4\\ = \left[ {\frac{{ - 3}}{{12}} + \frac{4}{{12}}} \right].4\\ = \frac{1}{{12}}.4 = \frac{1}{3}\end{array}$

d)

$\begin{array}{l}0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{1}{6} + \left( {\frac{{10}}{{42}} - \frac{{15}}{{42}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{7}{{42}} + \frac{{ - 5}}{{42}}} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\frac{1}{{21}}} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - \frac{1}{3}} \right\}\\ = \frac{4}{5}:\frac{{ - 2}}{{15}}\\ = \frac{4}{5}.\frac{{ - 15}}{2}\\ = - 6\end{array}$ $\begin{array}{l}0,8:\left\{ {0,2 - 7.\left[ {\frac{1}{6} + \left( {\frac{5}{{21}} - \frac{5}{{14}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{1}{6} + \left( {\frac{{10}}{{42}} - \frac{{15}}{{42}}} \right)} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\left[ {\frac{7}{{42}} + \frac{{ - 5}}{{42}}} \right]} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - 7.\frac{1}{{21}}} \right\}\\ = \frac{4}{5}:\left\{ {\frac{1}{5} - \frac{1}{3}} \right\}\\ = \frac{4}{5}:\frac{{ - 2}}{{15}}\\ = \frac{4}{5}.\frac{{ - 15}}{2}\\ = - 6\end{array}$

Bài 4 trang 26 Toán 7 tập 1 Cánh diều

Chọn dấu " "=", " $\ne$ $\ne$" thích hợp cho dấu “?” :

$a) \left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 ? 3,9 + \frac{1}{2} \cdot 2,6:13;$ $a) \left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 ? 3,9 + \frac{1}{2} \cdot 2,6:13;$

$b) \frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} ? {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2};$ $b) \frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} ? {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2};$

$c) \frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 ? \frac{{28}}{9} \cdot (0,7 + 0,5);$ $c) \frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 ? \frac{{28}}{9} \cdot (0,7 + 0,5);$

$d) \frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 ? \frac{{36}}{{13}}:(4 + 9).$ $d) \frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 ? \frac{{36}}{{13}}:(4 + 9).$

Hướng dẫn giải:

a)

$\begin{array}{l}\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{1}{2} \cdot \frac{{13}}{5}} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{{26}}{{10}}} \right).\frac{1}{{13}}\\ = \frac{{65}}{{10}}.\frac{1}{{13}} = \frac{1}{2}\end{array}$ $\begin{array}{l}\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{1}{2} \cdot \frac{{13}}{5}} \right):13\\ = \left( {\frac{{39}}{{10}} + \frac{{26}}{{10}}} \right).\frac{1}{{13}}\\ = \frac{{65}}{{10}}.\frac{1}{{13}} = \frac{1}{2}\end{array}$

$\begin{array}{l}3,9 + \frac{1}{2} \cdot 2,6:13\\ = \frac{{39}}{{10}} + \frac{1}{2}.\frac{{13}}{5}.\frac{1}{{13}}\\ = \frac{{39}}{{10}} + \frac{1}{{10}}\\ = \frac{{40}}{{10}} = 4\end{array}$ $\begin{array}{l}3,9 + \frac{1}{2} \cdot 2,6:13\\ = \frac{{39}}{{10}} + \frac{1}{2}.\frac{{13}}{5}.\frac{1}{{13}}\\ = \frac{{39}}{{10}} + \frac{1}{{10}}\\ = \frac{{40}}{{10}} = 4\end{array}$

Suy ra: $\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 \ne 3,9 + \frac{1}{2} \cdot 2,6:13$ $\left( {3,9 + \frac{1}{2} \cdot 2,6} \right):13 \ne 3,9 + \frac{1}{2} \cdot 2,6:13$

b)

$\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} = \frac{{20}}{{16}} - \frac{1}{{16}} = \frac{{19}}{{16}}$ $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} = \frac{{20}}{{16}} - \frac{1}{{16}} = \frac{{19}}{{16}}$

${\left( {\frac{5}{4} - \frac{1}{4}} \right)^2} = {1^2} = 1$ ${\left( {\frac{5}{4} - \frac{1}{4}} \right)^2} = {1^2} = 1$

Suy ra: $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} \ne {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2}$ $\frac{5}{4} - {\left( {\frac{1}{4}} \right)^2} \ne {\left( {\frac{5}{4} - \frac{1}{4}} \right)^2}$

c)

$\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 = \frac{{28}}{9}.\left( {0,7 + 0,5} \right)$ $\frac{{28}}{9} \cdot 0,7 + \frac{{28}}{9} \cdot 0,5 = \frac{{28}}{9}.\left( {0,7 + 0,5} \right)$

d)

$\begin{array}{l}\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\\ = \frac{{36}}{{13}}.\frac{1}{4} + \frac{{36}}{{13}}.\frac{1}{9}\\ = \frac{{36}}{{13}}.\left( {\frac{1}{4} + \frac{1}{9}} \right)\\ = \frac{{36}}{{13}}.\frac{{13}}{{36}} = 1\end{array}$ $\begin{array}{l}\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9\\ = \frac{{36}}{{13}}.\frac{1}{4} + \frac{{36}}{{13}}.\frac{1}{9}\\ = \frac{{36}}{{13}}.\left( {\frac{1}{4} + \frac{1}{9}} \right)\\ = \frac{{36}}{{13}}.\frac{{13}}{{36}} = 1\end{array}$

$\begin{array}{l}\frac{{36}}{{13}}:(4 + 9)\\ = \frac{{36}}{{13}}:13\\ = \frac{{36}}{{13}}.\frac{1}{{13}}\\ = \frac{{36}}{{169}}\end{array}$ $\begin{array}{l}\frac{{36}}{{13}}:(4 + 9)\\ = \frac{{36}}{{13}}:13\\ = \frac{{36}}{{13}}.\frac{1}{{13}}\\ = \frac{{36}}{{169}}\end{array}$

Suy ra $\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 \ne \frac{{36}}{{13}}:(4 + 9).$ $\frac{{36}}{{13}}:4 + \frac{{36}}{{13}}:9 \ne \frac{{36}}{{13}}:(4 + 9).$

Bài 4 trang 26 Toán 7 tập 1 Cánh diều

Tính một cách hợp lí:

$a) \frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right);$ $a) \frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right);$

$b) ( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3);$ $b) ( - 36,75) + \left( {\frac{{37}}{{10}} - 63,25} \right) - ( - 6,3);$

$c) 6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}};$ $c) 6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}};$

$d) ( - 39,1) \cdot \frac{{13}}{{25}} - 60,9 \cdot \frac{{13}}{{25}}.$ $d) ( - 39,1) \cdot \frac{{13}}{{25}} - 60,9 \cdot \frac{{13}}{{25}}.$

Hướng dẫn giải:

a) $\frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right)$ $\frac{4}{{15}} - \left( {2,9 - \frac{{11}}{{15}}} \right)$

$\begin{matrix} = \dfrac{4}{{15}} - 2,9 + \dfrac{{11}}{{15}} \hfill \\ = \left( {\dfrac{4}{{15}} + \dfrac{{11}}{{15}}} \right) - 2,9 \hfill \\ = \dfrac{{15}}{{15}} - 2,9 = 1 - 2,9 = - 1,9 \hfill \\ \end{matrix}$ $\begin{matrix} = \dfrac{4}{{15}} - 2,9 + \dfrac{{11}}{{15}} \hfill \\ = \left( {\dfrac{4}{{15}} + \dfrac{{11}}{{15}}} \right) - 2,9 \hfill \\ = \dfrac{{15}}{{15}} - 2,9 = 1 - 2,9 = - 1,9 \hfill \\ \end{matrix}$

b) $\left( { - 36,75} \right) + \left( {\frac{{37}}{{10}} - 63,25} \right) - \left( { - 6,3} \right)$ $\left( { - 36,75} \right) + \left( {\frac{{37}}{{10}} - 63,25} \right) - \left( { - 6,3} \right)$

$\begin{matrix} = - 36,75 + \dfrac{{37}}{{10}} - 63,25 + 6,3 \hfill \\ = - 36,75 - 63,25 + 3,7 + 6,3 \hfill \\ = - \left( {36,75 + 63,25} \right) + \left( {3,7 + 6,3} \right) \hfill \\ = - 100 + 10 = - 90 \hfill \\ \end{matrix}$ $\begin{matrix} = - 36,75 + \dfrac{{37}}{{10}} - 63,25 + 6,3 \hfill \\ = - 36,75 - 63,25 + 3,7 + 6,3 \hfill \\ = - \left( {36,75 + 63,25} \right) + \left( {3,7 + 6,3} \right) \hfill \\ = - 100 + 10 = - 90 \hfill \\ \end{matrix}$

c) $6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}}$ $6,5 + \left( { - \frac{{10}}{{17}}} \right) - \left( { - \frac{7}{2}} \right) - \frac{7}{{17}}$

$\begin{matrix} = 6,5 + 3,5 - \dfrac{7}{{17}} + \left( { - \dfrac{{10}}{{17}}} \right) \hfill \\ = \left( {6,5 + 3,5} \right) + \left[ { - \dfrac{7}{{17}} + \left( { - \dfrac{{10}}{{17}}} \right)} \right] \hfill \\ = 10 + \dfrac{{ - 17}}{{17}} = 10 - 1 = 9 \hfill \\ \end{matrix}$ $\begin{matrix} = 6,5 + 3,5 - \dfrac{7}{{17}} + \left( { - \dfrac{{10}}{{17}}} \right) \hfill \\ = \left( {6,5 + 3,5} \right) + \left[ { - \dfrac{7}{{17}} + \left( { - \dfrac{{10}}{{17}}} \right)} \right] \hfill \\ = 10 + \dfrac{{ - 17}}{{17}} = 10 - 1 = 9 \hfill \\ \end{matrix}$

d) $\left( { - 39,1} \right).\frac{{13}}{{25}} - 60,9.\frac{{13}}{{25}}$ $\left( { - 39,1} \right).\frac{{13}}{{25}} - 60,9.\frac{{13}}{{25}}$

$\begin{matrix} = \dfrac{{13}}{{25}}.\left[ { - 39,1 - 60,9} \right] \hfill \\ = \dfrac{{13}}{{25}}.\left( { - 100} \right) = - 52 \hfill \\ \end{matrix}$ $\begin{matrix} = \dfrac{{13}}{{25}}.\left[ { - 39,1 - 60,9} \right] \hfill \\ = \dfrac{{13}}{{25}}.\left( { - 100} \right) = - 52 \hfill \\ \end{matrix}$

Bài 5 trang 26 Toán 7 tập 1 Cánh diều

Một mảnh vườn có dạng hình chữ nhật với độ dài hai cạnh là 5,5 m và 3,75 m. Dọc theo các cạnh của mảnh vườn, người ta trồng các khóm hoa, cứ $\frac{1}{4}m$ $\frac{1}{4}m$ trồng một khóm hoa. Tính số khóm hoa cần trồng.

Hướng dẫn giải:

Chu vi mảnh vườn hình chữ nhật là:

$\left( {5,5 + 3,75} \right).2 = 18,5 (m)$ $\left( {5,5 + 3,75} \right).2 = 18,5 (m)$

Số khóm hoa cần trồng là:

$18,5:\frac{1}{4} = 74$ $18,5:\frac{1}{4} = 74$ (khóm)

Bài 6 trang 26 Toán 7 tập 1 Cánh diều

Cho miếng bìa có kích thước như hình vẽ bên (các số đo trên hình tính theo đơn vị đề-xi-mét).

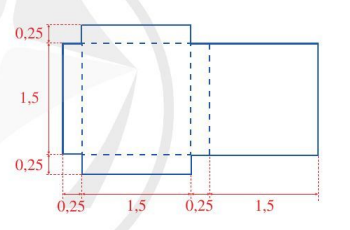
Bài 6 trang 26 Toán 7 tập 1 SGK Cánh Diều

a) Tính diện tích của miếng bìa.

b) Từ miếng bìa đó, người ta gấp thành một hình hộp chữ nhật. Tính thể tích của hình hộp chữ nhật đó.

Hướng dẫn giải:

a. Diện tích miếng bìa là: (0,25 + 1,5 + 0,25 + 1,5) . 1,5 + 2 . 0,25 . 1,5 = 6 (dm²)

b. Thể tích hình hộp chữ nhật là: 1,5 . 0,25 . 1,5 = 0,5625 (dm³)

Bài 7 trang 26 Toán 7 tập 1 Cánh diều

Trong đợt tri ân khách hàng, một cửa hàng bán xe đạp giảm giá 25% của giá niêm yết cho khách mua hàng. Cửa hàng vẫn được lãi 20% của giá nhập về đối với mỗi chiếc xe đạp bán ra. Tính giá nhập về và giá niêm yết của một chiếc xe đạp, biết rằng với mỗi chiếc xe đạp bán ra như thế, cửa hàng vẫn lãi được 600 000 đồng.

Hướng dẫn giải:

Giá nhập về của một chiếc xe đạp là:

$600\,\,000:\frac{{20}}{{100}} = 3\,\,000\,\,000$ $600\,\,000:\frac{{20}}{{100}} = 3\,\,000\,\,000$ (đồng)

Giá bán ra là: 3 000 000 + 600 000 =3 600 000 (đồng)

Do cửa hàng bán xe đạp giảm giá 25\% của giá niêm yết nên giá niêm yết bằng 125% giá bán ra.

Giá niêm yết là: $3 600 000 . \frac{{125}}{{100}} = 4 500 000$ $3 600 000 . \frac{{125}}{{100}} = 4 500 000$ (đồng)

Bài 8 trang 26 Toán 7 tập 1 Cánh diều

Một chủ cửa hàng bỏ ra 35 000 000 đồng mua gạo để bán. Vì kho chứa gạo bị hỏng nên khi phát hiện thì $\frac{1}{7}$ $\frac{1}{7}$ lượng gạo mua về đó đã bị giảm chất lượng, chủ cửa hàng đã bán số gạo còn lại với giá bán cao hơn 10% so với giá gạo lúc mua vào và đã bán số gạo bị giảm chất lượng với giá bán thấp hơn 25% so với giá gạo lúc mua vào.

a) Tính số tiền chủ cửa hàng thu về khi bán hết số gạo đó.

b) Chủ cửa hàng đã lãi hay lỗ bao nhiêu phần trăm?

Hướng dẫn giải:

a) Số gạo bị hỏng mua về có giá gốc là:

$\frac{1}{7}.35 000 000 = 5 000 000$ $\frac{1}{7}.35 000 000 = 5 000 000$ (đồng)

Số gạo không bị hỏng có giá gốc là:

35 000 000 – 5 000 000 = 30 000 000 (đồng)

Cửa hàng bán số gạo bị hỏng được số tiền là:

$5 000 000 .\frac{{75}}{{100}} = 3 750 000$ $5 000 000 .\frac{{75}}{{100}} = 3 750 000$ (đồng)

Cửa hàng bán số gạo không bị hỏng được số tiền là:

$30 000 000 . \frac{{110}}{{100}}= 33 000 000$ $30 000 000 . \frac{{110}}{{100}}= 33 000 000$ (đồng)

Số tiền cửa hàng thu về khi bán hết số gạo là:

3 750 000 + 33 000 000 =36 750 000 (đồng)

b) Chủ cửa hàng lãi số tiền là:

36 750 000 – 35 000 000 = 1 750 000 (đồng)

Chủ cửa hàng lãi:

$\frac{{1\,\,750\,\,000}}{{35\,000\,000}}.100\% = 5\%$ $\frac{{1\,\,750\,\,000}}{{35\,000\,000}}.100\% = 5\%$

Tải về

Chọn file muốn tải về: