Giải Toán 7 trang 86 tập 1 Kết nối tri thức
Giải Toán 7 trang 86 Tập 1
Giải Toán 7 trang 86 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 7 Kết nối tri thức tập 1 trang 86.
Bài 4.29 trang 86 Toán 7 tập 1 Kết nối
Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ.
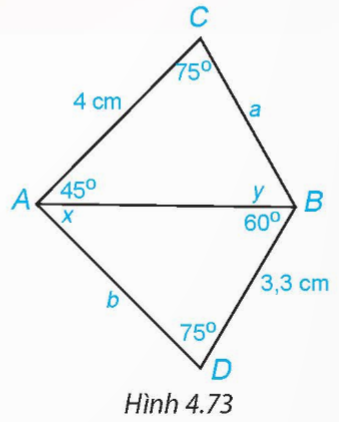
Hướng dẫn giải:
Xét tam giác ABC có: 
\(\widehat {CAB} + \widehat {ABC} + \widehat {BCA} = {180^0}\)
⇒ \(\widehat {ABC} = {180^0} - \left( {\widehat {CAB} + \widehat {BCA}} \right)\)
⇒ \(y = {180^0} - \left( {{{45}^0} + {{75}^0}} \right) = {60^0}\)
Xét tam giác ABD có: \(\widehat {BAD} + \widehat {ADB} + \widehat {DBA} = {180^0}\)
⇒ \(\widehat {BAD} = {180^0} - \left( {\widehat {ADB} + \widehat {DBA}} \right)\)
⇒ \(x = {180^0} - \left( {{{75}^0} + {{60}^0}} \right) = {45^0}\)
Xét ∆ ABC và ∆ ABD ta có:
\(\widehat {CAB} = \widehat {DAB} = {45^0}\)
AB là cạnh chung
\(\widehat {CBA} = \widehat {DBA} = {60^0}\)
Do đó ∆ ABC = ∆ ABD (g – c – g)
⇒ AC = AD = 4 cm hay b = 4 cm
⇒ CB = BD = 3,3 cm hay a = 3,3 cm
Bài 4.30 trang 86 Toán 7 tập 1 Kết nối
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:
a) ∆ OAN = ∆ OBM
b) ∆ AMN = ∆ BNM
Hướng dẫn giải:
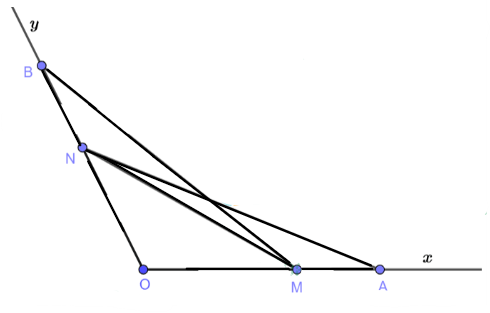
a) Xét ∆ OAN và ∆ OBM ta có:
OA = OB (giả thiết)
ON = OM (giả thiết)
Góc \(\widehat O\) chung
Do đó ∆ OAN = ∆ OBM (c – g – c)
b) Ta có: ∆ OAN = ∆ OBM ⇒ MB = AN (hai cạnh tương ứng)
Mặt khác: OA = MA + OM ⇒ MA = OA – OM (1)
OB = NB + ON ⇒ NB = OB – ON (2)
Mà OA = OB, ON = OM (3)
Từ (1), (2), (3) ⇒ MA = NB
Xét ∆ AMN và ∆ BNM ta có:
MA = NB
NA = BM (cmt)
MN là cạnh chung
Do đó ∆ AMN = ∆ BNM (c – g – c)
Bài 4.31 trang 86 Toán 7 tập 1 Kết nối
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
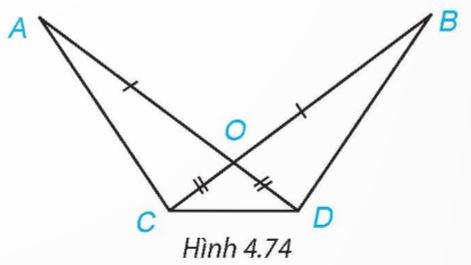
a) AC = BD;
b) ∆ ACD = ∆ BDC.
Hướng dẫn giải:
a) Xét ∆ ACO và ∆ BDO ta có:
OA = OB (gt)
\(\widehat {AOC} = \widehat {BOD}\)(hai góc đối đỉnh)
OC = OD (gt)
⇒ ∆ ACO = ∆ BDO (c – g – c)
⇒ AC = BD (hai cạnh tương ứng)
b) Ta có: OA = OB
OD = OC
⇒ OA + OD = OB + OC
⇒ AD = BC
Xét tam giác ACD và tam giác BDC ta có:
CD là cạnh chung
AC = BD (cma)
AD = BC (cmt)
⇒ ∆ ACD = ∆ BDC (c – c – c)
Bài 4.32 trang 86 Toán 7 tập 1 Kết nối
Cho tam giác MBC vuông tại M có \(\widehat B = 60^{\circ}\). Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.
Hướng dẫn giải:
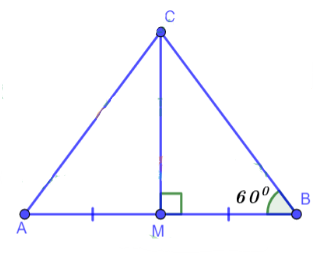
Ta có: A nằm trên tia đối của tia MB ⇒ Ba điểm A, M, B thẳng hàng
Mà ∆ CMB vuông tại M nên CM ⊥ MB ⇒ CM ⊥ AB
Mặt khác: AM = MB
⇒ CM là đường trung trực của đoạn thẳng AB
⇒ CA = CB ⇒ ∆ ABC cân tại C
Lại có \(\widehat B = {60^0}\)
⇒ ∆ ABC là tam giác đều.
-----------------------------------------------
Lời giải Toán 7 trang 86 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 7 Kết nối tri thức bài Luyện tập chung trang 85, được VnDoc biên soạn và đăng tải!
