Toán 7 Bài 15: Các trường hợp bằng nhau của tam giác vuông
Giải bài tập Toán 7 trang 79 Kết nối tri thức
1. Ba trường hợp bằng nhau của tam giác vuông
Hoạt động 1 trang 75 Toán 7 Tập 1
Hai tam giác vuông ABC (vuông tại đỉnh A) và A’B’C’ (vuông tại đỉnh A’) có các cặp cạnh góc vuông bằng nhau: AB = A'B', AC = A'C' (H.4.45). Dựa vào trường hợp bằng nhau cạnh - góc - cạnh của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
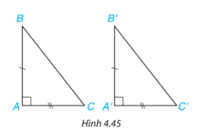
Hướng dẫn giải:
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'} (gt)\)
AC=A’C’ (gt)
\(\Rightarrow \Delta ABC = \Delta A'B'C'(c.g.c)\)
Hoạt động 2 trang 76 Toán 7 Tập 1
\(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và ABC bằng nhau.
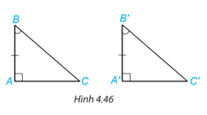
Hướng dẫn giải:
Xét 2 tam giác ABC và A'B'C' có:
\(\widehat B = \widehat {B'} (gt)\)
AB=A’B’ (gt)
\(\widehat A = \widehat {A'} (gt)\)
\(\Rightarrow \Delta ABC = \Delta A'B'C'(g.c.g)\)
Luyện tập 1 trang 76 Toán 7 Tập 1
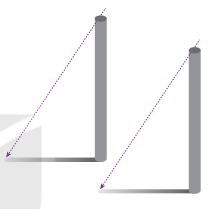
Hướng dẫn giải:
Lí do mà bạn Tròn đưa ra là đúng. Vì hai tam giác vuông này bằng nhau ( g-c-g)
Hoạt động 3 trang 76 Toán 7 Tập 1
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B’C’ và các góc B, B’. Khi đó AC, A’C’ mô tả độ cao của hai con dốc.
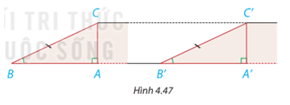
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
Hướng dẫn giải:
a)Xét hai tam giác vuông ABC và A’B’C’ có:
BC=B’C’ (gt)
\(\widehat {ABC} = \widehat {A'B'C'} (gt)\)
\(\Rightarrow \Delta ABC = \Delta A'B'C'\)(cạnh huyền – góc nhọn)
b)Do \(\Delta ABC = \Delta A'B'C'\) nên AC=A’C’ ( 2 cạnh tương ứng)
Vậy độ cao hai con dốc bằng nhau.
Câu hỏi trang 77 Toán 7 Tập 1
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
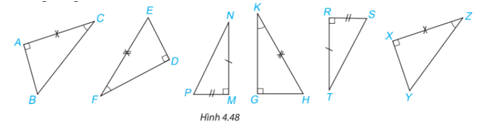
Hướng dẫn giải:
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ ) (gt)\)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\(\Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
EF = HK (gt)
\(\widehat {EFD} = \widehat {GKH} (gt)\)
\(\Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
MN = TR (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
PM = SR (gt)
\(\Rightarrow \Delta MNP = \Delta RTS (c.g.c)\)
Luyện tập 2 trang 77 Toán 7 Tập 1
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
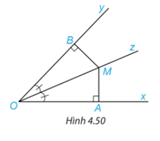
Hướng dẫn giải:
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM} (gt)\)
\(\Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
2. Trường hợp bằng nhau đặc biệt của tam giác vuông
Hoạt động 4 trang 78 Toán 7 Tập 1
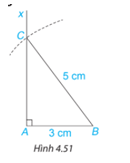
Vẽ tam giác vuông ABC có A = 90°, AB = 3 cm, BC = 5 cm theo các bước sau:
• Dùng thước thẳng có vạch chia vẽ đoạn thẳng AB = 3 cm.
• Vẽ tia Ax vuông góc với AB và cung tròn tâm B bán kính 5 cm như Hình 4.51.
Cung tròn cắt tia Ax tại điểm C.
•Vẽ đoạn thẳng BC ta được tam giác ABC.
Hướng dẫn giải:
Hoạt động 5 trang 78 Toán 7 Tập 1
Tương tự, vẽ thêm tam giác ABC có A = 90°, AB = 3 cm, BC = 5 cm.
a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra xem AC có bằng A'C' không?
b) Hai tam giác ABC và A'B'C' có bằng nhau không?
Hướng dẫn giải:
a) Dùng thước thẳng có vạch chia hoặc compa kiểm tra được AC = A'C'
b) Hai tam giác ABC và A'B'C' có bằng nhau vì 3 cặp cạnh đều bằng nhau
Câu hỏi trang 78 Toán 7 Tập 1
Hãy chỉ ra các cặp tam giác vuông bằng nhau dưới đây.
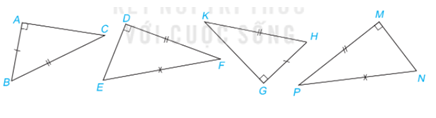
Hướng dẫn giải:
Xét hai tam giác ABC vuông tại A và GHK vuông tại G có:
AB = GH (gt)
BC = HK (gt)
Do đó Δ A B C = Δ G H K (cạnh huyền – cạnh góc vuông).
Xét hai tam giác DEF vuông tại D và MNP vuông tại M có:
DF = MP (gt)
EF = NP (gt)
Do đó Δ D EF = Δ M N P (cạnh huyền – cạnh góc vuông).
Vậy Δ A B C = Δ G H K , Δ D EF = Δ M N P .
Luyện tập 3 trang 79 Toán 7 Tập 1
Cho ba điểm A, B, C nằm trên đường tròn tâm O và các điểm M, N, P như Hình 4.54. Hãy chỉ ra ba cặp tam giác vuông bằng nhau trong hình.
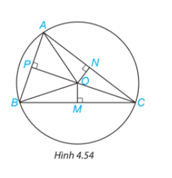
Hướng dẫn giải:
Vì A, B, C nằm trên đường tròn tâm O nên OA = OB = OC.
Xét hai tam giác ONA vuông tại N và ONC vuông tại N có:
OA = OC (cmt)
ON chung
Do đó Δ O N A = Δ O N C (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OMB vuông tại M và OMC vuông tại M có:
OB = OC (cmt)
OM chung
Do đó Δ O M B = Δ O M C (cạnh huyền – cạnh góc vuông).
Xét hai tam giác OPA vuông tại P và OPB vuông tại P có:
OA = OB (cmt)
OP chung
Do đó Δ OPA = Δ OPB (cạnh huyền – cạnh góc vuông).
Giải bài tập trang 79 Toán 7 tập 1 KNTT
Bài 4.20 trang 79 Toán 7 tập 1 KNTT
Mỗi hình sau có các cặp tam giác vuông nào bằng nhau? Vì sao?
Hướng dẫn giải:
a) Xét 2 tam giác vuông ABC và ADC có:
\(\widehat {ACB} = \widehat {ACD}( = 90^\circ )\)
AC chung
\(\widehat {BAC} = \widehat {DAC}(gt)\)
\(=>\Delta ABC = \Delta ADC(g.c.g)\)
b) Xét 2 tam giác vuông HEG và GFH có:
HE=GF(gt)
HG chung
\(=>\Delta HEG = \Delta GFH(c.h-c.g.v)\)
c) Xét 2 tam giác vuông QMK và NMP có:
QK=NP
\(\widehat K = \widehat P\)
\(=>\Delta QMK = \Delta NMP\)(cạnh huyền – góc nhọn)
d) Xét 2 tam giác vuông VST và UTS có:
VS=UT
ST chung
\(=>\Delta VST = \Delta UTS(c.g.c)\)
Bài 4.21 trang 79 Toán 7 tập 1 KNTT
Cho hình 4.56, biết \(AB=CD, \widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).
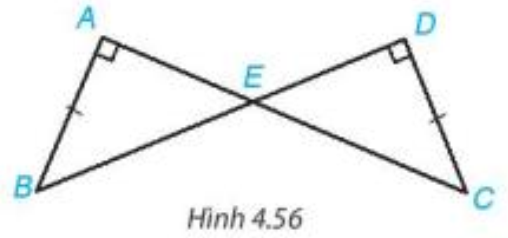
Hướng dẫn giải:
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AED và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {AEB} = \widehat {DEC}\)
Xét 2 tam giác vuông AEB và DEC có:
AB=DC
\(\widehat {AEB} = \widehat {DEC}\)
\(=>\Delta AEB = \Delta DEC(g.c.g)\)
Bài 4.22 trang 79 Toán 7 tập 1 KNTT
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC.
Chứng minh rằng \(\Delta ABM = \Delta DCM\).
Hướng dẫn giải:
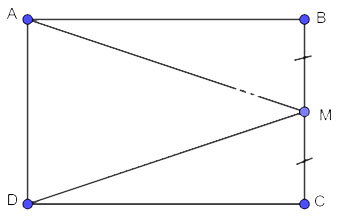
Xét 2 tam giác vuông ABM và DCM có:
AB=DC (tính chất hình chữ nhật)
BM=CM (gt)
\(=>\Delta ABM = \Delta DCM(c.g.c)\)
