Giải Toán 7 trang 81 tập 1 Kết nối tri thức

Giải Toán 7 trang 81 Tập 1

Hoạt động 1 trang 81 Toán 7 tập 1 Kết nối
Hoạt động 2 trang 81 Toán 7 tập 1 Kết nối
Luyện tập 1 trang 81 Toán 7 tập 1 Kết nối
Hoạt động 3 trang 81 Toán 7 tập 1 Kết nối

Giải Toán 7 trang 81 Tập 1 Kết nối tri thức hướng dẫn giải chi tiết cho các câu hỏi và bài tập trong SGK Toán 7 Kết nối tri thức tập 1 trang 81.

Hoạt động 1 trang 81 Toán 7 tập 1 Kết nối

Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.

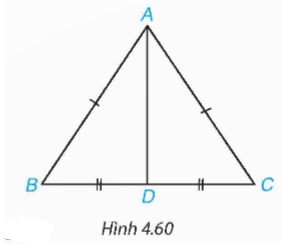
a) Chứng minh rằng Δ ABD = Δ ACD theo trường hợp cạnh – cạnh – cạnh.

b) Hai góc B và C của tam giác ABC có bằng nhau không?

Hướng dẫn giải:

a) Xét Δ ABD và Δ ACD có:

AB = AC (Δ ABC cân tại A)

AD chung

BD = CD (D là trung điểm của BC)

⇒ Δ ABD = Δ ACD (c – c – c)

b) Ta có: Δ ABD = Δ ACD (cm a)

Suy ra $\widehat {ABD} = \widehat {ACD}$ $\hat{A B D} = \hat{A C D}$ hay $\widehat {ABC} = \widehat {ACB}$ $\hat{A B C} = \hat{A C B}$ (hai góc tương ứng)

Hoạt động 2 trang 81 Toán 7 tập 1 Kết nối

Cho tam giác MNP có $\widehat M = \widehat N$ $\hat{M} = \hat{N}$ . Vẽ tia phân giác PK của góc MPN (K ∈ MN).

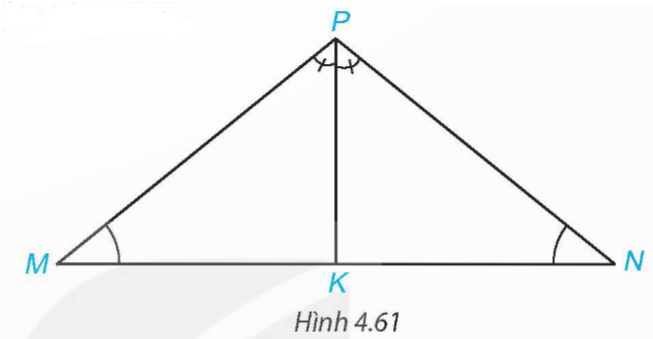
Chứng minh rằng:

a) $\widehat {MKP} = \widehat {NKP}$ $\hat{M K P} = \hat{N K P}$

b) Δ MPK = Δ NPK

c) Tam giác MNP có cân tại P không?

Hướng dẫn giải:

a) Xét tam giác MPK ta có:

$\widehat {MPK} + \widehat {PMK} + \widehat {MKP} = {180^0}$ $\hat{M P K} + \hat{P M K} + \hat{M K P} = 180^{0}$

$\Rightarrow \widehat {MKP} = {180^0} - \left( {\widehat {MPK} + \widehat {PMK}} \right)$ $\Rightarrow \hat{M K P} = 180^{0} - (\hat{M P K} + \hat{P M K})$

Xét tam giác NPK ta có:

$\widehat {NPK} + \widehat {PNK} + \widehat {NKP} = {180^0}$ $\hat{N P K} + \hat{P N K} + \hat{N K P} = 180^{0}$

$\Rightarrow \widehat {NKP} = {180^0} - \left( {\widehat {NPK} + \widehat {PNK}} \right)$ $\Rightarrow \hat{N K P} = 180^{0} - (\hat{N P K} + \hat{P N K})$

Mà PK là tia phân giác của góc MPN ⇒ $\widehat {MPK} = \widehat {NPK}$ $\hat{M P K} = \hat{N P K}$

Mặt khác $\widehat {PMK} = \widehat {PNK}$ $\hat{P M K} = \hat{P N K}$ (gt)

⇒ $\widehat {MKP} = \widehat {NKP}$ $\hat{M K P} = \hat{N K P}$

b) Xét Δ MPK và Δ NPK ta có:

PK là cạnh chung

$\widehat {MPK} = \widehat {NPK}$ $\hat{M P K} = \hat{N P K}$

$\widehat {MKP} = \widehat {NKP}$ $\hat{M K P} = \hat{N K P}$

⇒ Δ MPK = Δ NPK (g . c . g)

c) Do Δ MPK = Δ NPK ⇒ PM = PN (hai cạnh tương ứng).

Tam giác MNP có PM = PN hay MNP là tam giác cân tại P

Luyện tập 1 trang 81 Toán 7 tập 1 Kết nối

Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.

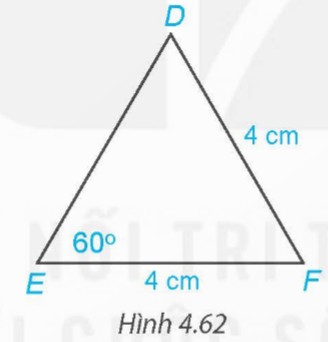
Hướng dẫn giải:

Tam giác FDE có FD = FD = 4 cm nên Δ FDE cân tại F

Suy ra $\widehat D = \widehat E = {60^0}$ $\hat{D} = \hat{E} = 60^{0}$

Xét tam giác FDE có $\widehat D + \widehat E + \widehat F = {180^0}$ $\hat{D} + \hat{E} + \hat{F} = 180^{0}$ (định lí tổng các góc trong một tam giác)

⇒ $\widehat F = {180^0} - \left( {\widehat D + \widehat E} \right)$ $\hat{F} = 180^{0} - (\hat{D} + \hat{E})$

$\Rightarrow \widehat F = {180^0} - \left( {{{60}^0} + {{60}^0}} \right) = {60^0}$ $\Rightarrow \hat{F} = 180^{0} - (60^{0} + 60^{0}) = 60^{0}$

Xét tam giác DEF có: $\widehat D=\widehat F = \widehat E = {60^0}$ $\hat{D} = \hat{F} = \hat{E} = 60^{0}$ nên tam giác DEF đều

Vậy DE = DF = 4 cm.

Hoạt động 3 trang 81 Toán 7 tập 1 Kết nối

Đánh dấu hai điểm a và B nằm trên hai mép tờ giấy A4, nối A và B để được đoạn thẳng AB.

Gấp mảnh giấy lại như Hình 4.63 sao cho vị trí các điểm A và B trùng nhau.

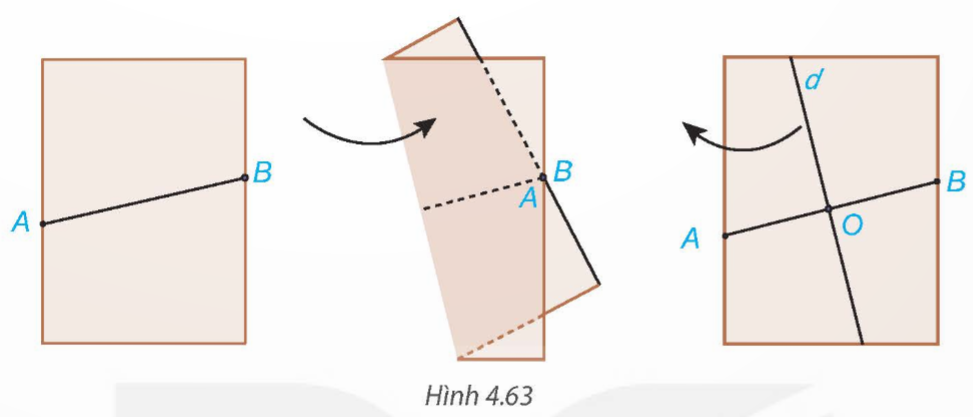
Mở mảnh giấy ra, kẻ một đường thẳng d theo nếp gấp.

a) Gọi O là giao điểm của đường thẳng d và AB. O có là trung điểm của đoạn thẳng AB không?

b) Dùng thước đo góc, kiểm tra đường thẳng d có vuông góc với AB không?

Hướng dẫn giải:

Thực hiện gấp giấy như đề bài. Nhận xét:

a) O có là trung điểm của đoạn thẳng AB.

b) Đường thẳng d vuông góc với đoạn thẳng AB.

-----------------------------------------------

Lời giải Toán 7 trang 81 Tập 1 Kết nối tri thức với các câu hỏi nằm trong Giải Toán 7 Kết nối tri thức bài Tam giác cân. Đường trung trực của đoạn thẳng, được VnDoc biên soạn và đăng tải!

Chia sẻ, đánh giá bài viết

1

140

Bài trước

Bài sau

Chia sẻ bởi:
Lê Jelar

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!