Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Toán 7 Luyện tập chung trang 68

Giải Toán 7 Kết nối tri thức

Bài trước

Tải về

Bài sau

Lớp: Lớp 7

Môn: Toán

Dạng tài liệu: Giải bài tập

Bộ sách: Kết nối tri thức với cuộc sống

Loại File: PDF

Phân loại: Tài liệu Tính phí

Giải Toán 7: Luyện tập chung trang 68 được biên soạn nhằm đồng hành cùng các em học sinh trong lộ trình chinh phục chương trình SGK Kết nối tri thức với cuộc sống (Tập 1). Với hệ thống lời giải chi tiết và phương pháp tiếp cận hiện đại cho các bài tập tại trang 69, nội dung này giúp các em tổng hợp lại toàn bộ kiến thức trọng tâm đã học. Qua việc thực hành các dạng toán đa dạng, học sinh không chỉ củng cố vững chắc lý thuyết mà còn rèn luyện kỹ năng tính toán chuẩn xác và tư duy logic. Đây là nguồn tham khảo hữu ích giúp các em tự tin đạt kết quả cao trong các bài kiểm tra. Mời các em cùng theo dõi chi tiết!

Bài 4.7 trang 69 Toán 7 tập 1 KNTT

Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?

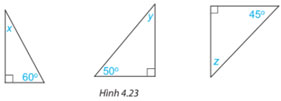
Bài 4.7

Hướng dẫn giải:

Ta có:

$x + {60^o} = {90^o} \Rightarrow x = {30^o}$

$y + {50^o} = {90^o} \Rightarrow y = {40^o}$

$z + {45^o} = {90^o} \Rightarrow z = {45^o}$

Bài 4.8 trang 69 Toán 7 tập 1 KNTT

Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.

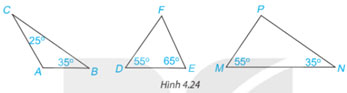
Bài 4.8

Hướng dẫn giải:

Ta có:

$\widehat A + \widehat B + \widehat C = {180^o}$ (Định lí tổng 3 góc trong một tam giác)

$\Rightarrow \widehat A + {25^o} + {35^o} = {180^o} \Rightarrow \widehat A = {120^o}$

$\widehat D + \widehat E + \widehat F = {180^o}$ (Định lí tổng 3 góc trong một tam giác)

$\Rightarrow {55^o} + {65^o} + \widehat F = {180^o} \Rightarrow \widehat F = {60^o}$

$\widehat M + \widehat N + \widehat P = {180^o}$ (Định lí tổng 3 góc trong một tam giác)

$\Rightarrow {55^o} + {35^o} + \widehat P = {180^o} \Rightarrow \widehat P = {90^o}$

Vậy tam giác MNP vuông tại P

Bài 4.9 trang 69 Toán 7 tập 1 KNTT

Cho Hình 4.25, biết $\widehat {DAC} = {60^\circ },AB = AC,DB = DC$ . Hãy tính $\widehat {DAB}$ .

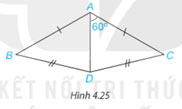
Hình 4.25

Hướng dẫn giải:

Xét hai tam giác ADB và ADC có:
AB = AC (theo giả thiết).

BD = CD (theo giả thiết).

AD chung.

$\Rightarrow \Delta ADB = ADC(c.c.c)$

$\Rightarrow \widehat {DAB} = \widehat {DAC} = {60^o}$

Bài 4.10 trang 69 Toán 7 tập 1 KNTT

Cho tam giác ABC có $\widehat {BCA} = {60^o}$ và điểm M nằm trên cạnh BC sao cho $\widehat {BAM} = {20^\circ },\widehat {AMC} = {80^\circ }({\rm{H}}.4.26)$ . Tính số đo các góc AMB, ABC, BAC

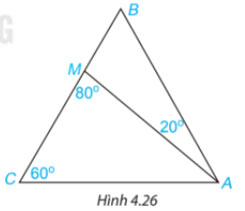
Hình 4.26

Hướng dẫn giải:

Ta có:

$\widehat {AMB} + \widehat {AMC} = {180^o}$ (2 góc kề bù)

$\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}$

+) Xét tam giác AMB có:

$\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}$

+) Xét tam giác ABC có:

$\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}$

Bài 4.11 trang 69 Toán 7 tập 1 KNTT

Cho $\Delta ABC = \Delta DEF$ . Biết rằng $\widehat A = {60^\circ },\hat E = {80^\circ }$ , tính số đo các góc B, C, D, F.

Hướng dẫn giải:

Do $\Delta ABC = \Delta DEF$ nên:

$\widehat B = \widehat E = {80^o}$

$\widehat D = \widehat A = {60^o}$

Xét tam giác ABC có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 60^\circ + 80^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 60^\circ - 80^\circ = 40^\circ \end{array}$

Do 2 tam giác $\Delta ABC = \Delta DEF$ nên $\widehat C = \widehat F = 40^\circ$ (2 góc tương ứng)

Tải về

Chọn file muốn tải về: