Toán 7 bài 2: Đại lượng tỉ lệ thuận

Giải Toán 7 Chân trời sáng tạo

Mời các bạn tham khảo Giải Toán 7 Bài 2: Đại lượng tỉ lệ thuận sách Chân trời sáng tạo bao gồm lời giải và đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 2 chương trình sách mới. Lời giải Toán 7 được trình bày chi tiết, dễ hiểu, giúp các em học sinh ôn tập, củng cố kiến thức được học trong bài 1 chương 6 Toán 7. Sau đây mời các bạn tham khảo chi tiết.

Giải Toán 7 Chân trời sáng tạo trang 14, 15 tập 2

Khám phá 1 trang 11 Toán lớp 7 Tập 2:
Thực hành 1 trang 11 Toán lớp 7 Tập 2:
Vận dụng 1 trang 11 Toán lớp 7 Tập 2:
Hoạt động 2 trang 12 Toán lớp 7 Tập 2:
Thực hành 2 trang 11 Toán lớp 7 Tập 2:
Vận dụng 2 trang 13 Toán lớp 7 Tập 2:
Bài 1 trang 14 SGK Toán 7 tập 1
Bài 2 trang 14 SGK Toán 7 tập 1
Bài 3 trang 14 SGK Toán 7 tập 1
Bài 4 trang 14 SGK Toán 7 tập 1
Bài 5 trang 14 SGK Toán 7 tập 1
Bài 6 trang 15 SGK Toán 7 tập 1
Bài 7 trang 14 SGK Toán 7 tập 1
Bài 8 trang 14 SGK Toán 7 tập 1
Bài 9 trang 14 SGK Toán 7 tập 1

Khám phá 1 trang 11 Toán lớp 7 Tập 2:

a) Học sinh trường Nguyễn Huệ tham gia phong trào “Trồng cây xanh bảo vệ môi trường”, mỗi em đều trồng được 4 cây. Gọi c là số cây trồng được, h là số học sinh đã tham gia. Em hãy viết công thức tính c theo h.

b) Tìm điểm giống nhau giữa hai công thức y = 10x và c = 4h.

Hướng dẫn giải:

a) Do mỗi em trồng được 4 cây, có h em học sinh tham gia nên số cây trồng được là 4h cây.

Do đó c = 4h.

b) Trong hai công thức này, có 1 đại lượng gấp k lần đại lượng còn lại (k ≠ 0).

Thực hành 1 trang 11 Toán lớp 7 Tập 2:

a) Cho hai đại lượng f và x liên hệ với nhau theo công thức f = 5x. Hãy cho biết đại lượng x có tỉ lệ thuận với đại lượng f hay không. Hệ số tỉ lệ là bao nhiêu?

b) Cho đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8. Hãy viết công thức tính P theo m.

Hướng dẫn giải

a) Ta có: f = 5x => $x = \frac{f}{5} = \frac{1}{5}f$ $x = \frac{f}{5} = \frac{1}{5}f$

=> Đại lượng x tỉ lệ thuận với đại lượng f với hệ số tỉ lệ là $\frac{1}{5}$ $\frac{1}{5}$

b) Ta có: Đại lượng P tỉ lệ thuận với đại lượng m theo hệ số tỉ lệ g = 9,8

=> P = 9,8 . m

Vận dụng 1 trang 11 Toán lớp 7 Tập 2:

Cho biết khối lượng mỗi mét khối của một số kim loại như sau: đồng: 8 900 kg; vàng: 19 300 kg; bạc: 10 500 kg.

Hãy viết công thức tính khối lượng m (kg) theo thể tích V (m³) của mỗi kim loại và cho biết m tỉ lệ thuận với V theo hệ số tỉ lệ là bao nhiêu.

Hướng dẫn giải

Với kim loại đồng ta có mỗi m³ đồng có khối lượng 8 900 kg

=> m = 8 900.V

Với kim loại vàng ta có mỗi m³ vàng có khối lượng 19 300 kg

=> m = 19 300.V

Với kim loại bạc ta có mỗi m³ đồng có khối lượng 10 500 kg

=> m = 10 500.V

Hoạt động 2 trang 12 Toán lớp 7 Tập 2:

Cho biết giá trị tương ứng của hai đại lượng y và x tỉ lệ thuận với nhau trong bảng sau:

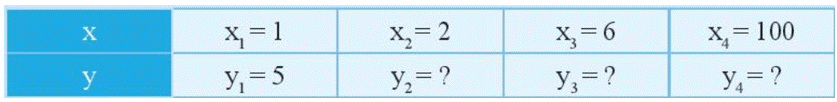
Hoạt động 2 trang 12 Toán 7 tập 2 SGK Chân trời sáng tạo

a) Hãy xác định hệ số tỉ lệ của y đối với x.

b) Tính các giá trị tương ứng chưa biết của y.

c) So sánh các tỉ số giữa hai giá trị tương ứng của y và x. $\frac{{{y_1}}}{{{x_1}}};\frac{{{y_2}}}{{{x_2}}};\frac{{{y_3}}}{{{x_3}}};\frac{{{y_4}}}{{{x_4}}}$ $\frac{{{y_1}}}{{{x_1}}};\frac{{{y_2}}}{{{x_2}}};\frac{{{y_3}}}{{{x_3}}};\frac{{{y_4}}}{{{x_4}}}$

Hướng dẫn giải

a) Đại lượng y tỉ lệ thuận với đại lượng x và y₁= 5x₁nên hệ số tỉ lệ của y đối với x là 5.

b) Ta có: Hệ số tỉ lệ của y đối với x là 5 ta có:

Với x₂ = 2 => y₂ = 5.2 = 10

Với x₃ = 6 => y₃ = 5.6 = 30

Với x₄ = 100 => y₄ = 5.100 = 500

c) Ta có:

$\begin{matrix} \dfrac{{{y_1}}}{{{x_1}}} = \dfrac{5}{1} = 5 \hfill \\ \dfrac{{{y_2}}}{{{x_2}}} = \dfrac{{10}}{2} = 5 \hfill \\ \dfrac{{{y_3}}}{{{x_3}}} = \dfrac{{30}}{6} = 5 \hfill \\ \dfrac{{{y_4}}}{{{x_4}}} = \dfrac{{500}}{{100}} = 5 \hfill \\ \end{matrix}$ $\begin{matrix} \dfrac{{{y_1}}}{{{x_1}}} = \dfrac{5}{1} = 5 \hfill \\ \dfrac{{{y_2}}}{{{x_2}}} = \dfrac{{10}}{2} = 5 \hfill \\ \dfrac{{{y_3}}}{{{x_3}}} = \dfrac{{30}}{6} = 5 \hfill \\ \dfrac{{{y_4}}}{{{x_4}}} = \dfrac{{500}}{{100}} = 5 \hfill \\ \end{matrix}$

Tỉ số giữa hai giá trị tương ứng của y và x bằng nhau và bằng 5.

Thực hành 2 trang 11 Toán lớp 7 Tập 2:

Trong các trường hợp sau, hãy kiểm tra xem hai đại lượng m và n có tỉ lệ thuận với nhau hay không.

a)

m	2	4	6	8	10
n	4	16	36	64	100

b)

m	1	2	3	4	5
n	-5	-10	-15	-20	-25

Hướng dẫn giải

a) Với n = 4 , m = 2 => $\frac{n}{m} = \frac{4}{2} = 2$ $\frac{n}{m} = \frac{4}{2} = 2$

với n = 16; m = 4 => $\frac{n}{m} = \frac{{16}}{4} = 4 \ne 2$ $\frac{n}{m} = \frac{{16}}{4} = 4 \ne 2$

vậy m và n không là hai đại lượng tỉ lệ thuận với nhau.

b) Với n = -5, m = 1 => $\frac{n}{m} = \frac{{ - 5}}{1} = - 5$ $\frac{n}{m} = \frac{{ - 5}}{1} = - 5$

Với n = -10; m = 2 => $\frac{n}{m} = \frac{{ - 10}}{2} = - 5$ $\frac{n}{m} = \frac{{ - 10}}{2} = - 5$

Với n = -15; m = 3 => $\frac{n}{m} = \frac{{ - 15}}{2} = - 5$ $\frac{n}{m} = \frac{{ - 15}}{2} = - 5$

Với n = -20; m = 4 => $\frac{n}{m} = \frac{{ - 20}}{2} = - 5$ $\frac{n}{m} = \frac{{ - 20}}{2} = - 5$

Với n = -25; m = 5 => $\frac{n}{m} = \frac{{ - 25}}{2} = - 5$ $\frac{n}{m} = \frac{{ - 25}}{2} = - 5$

Vậy m và n là hai đại lượng tỉ lệ thuận với nhau

Hệ số tỉ lệ k của n đối với m là -5

Vận dụng 2 trang 13 Toán lớp 7 Tập 2:

Cho biết hai đại lượng m và n tỉ lệ thuận với nhau. Hãy tìm giá trị của a và b.

m	2	3	4	b
n	-6	-9	a	-18

Hướng dẫn giải

Với m = 2, n = -6 => $\frac{n}{m} = \frac{{ - 6}}{2} = - 3$ $\frac{n}{m} = \frac{{ - 6}}{2} = - 3$

Hai đại lượng m và n tỉ lệ thuận với nhau

=> Hệ số tỉ lệ của n đối với m là -3

Với m = 4; n = a => $\frac{n}{m} = \frac{a}{4} = - 3 \Rightarrow a = 4.\left( { - 3} \right) = - 12$ $\frac{n}{m} = \frac{a}{4} = - 3 \Rightarrow a = 4.\left( { - 3} \right) = - 12$

Với n = -18, m = b => $\frac{n}{m} = \frac{{ - 18}}{b} = - 3 \Rightarrow b = \frac{{ - 18}}{{ - 3}} = 6$ $\frac{n}{m} = \frac{{ - 18}}{b} = - 3 \Rightarrow b = \frac{{ - 18}}{{ - 3}} = 6$

Hoàn thành bảng số liệu như sau:

m	2	3	4	6
n	-6	-9	-12	-18

Bài 1 trang 14 SGK Toán 7 tập 1

Cho hai đại lượng a và b tỉ lệ thuận với nhau. Biết rằng khi a = 2 thì b = 18.

a. Tìm hệ số tỉ lệ k của a đối với b.

b. Tính giá trị của b khi a = 5.

Hướng dẫn giải:

a) Do a tỉ lệ thuận với b theo hệ số tỉ lệ k, nên a = k.b

Suy ra: $k=\frac{a}{b}=\frac{2}{18}=\frac{1}{9}$ $k=\frac{a}{b}=\frac{2}{18}=\frac{1}{9}$.

b) Theo a, ta có: $a=\frac{1}{9}.b$ $a=\frac{1}{9}.b$

$\Rightarrow b = 9. a = 9. 5 = 45$ $\Rightarrow b = 9. a = 9. 5 = 45$

Bài 2 trang 14 SGK Toán 7 tập 1

Hai cho hai đại lượng x và y tỉ lệ thuận với nhau biết biết rằng khi x = 7 thì y = 21.

a. Tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x.

b. Tìm hệ số tỉ lệ của x đối với y và biểu diễn x theo y.

Hướng dẫn giải:

a) Hệ số tỉ lệ của y đối với x là: k = 21 : 7 = 3.

Vậy ta có: y = 3. x

b) Hệ số tỉ lệ của x đối với y là: .

Vậy ta có: $x = \frac{1}{3}y$ $x = \frac{1}{3}y$.

Bài 3 trang 14 SGK Toán 7 tập 1

Cho m và n là hai đại lượng tỉ lệ thuận với nhau. Hãy viết công thức tính m theo n và tính các giá trị chưa biết trong bảng sau:

n	-2	-1	0	1	2
m	?	?	?	-5	?

Giải

Với n = -1; m = -5 => $\frac{m}{n} = \frac{{ - 5}}{1} = - 5$ $\frac{m}{n} = \frac{{ - 5}}{1} = - 5$

Do m và n là hai đại lượng tỉ lệ thuận với nhau

=> Hệ số tỉ lệ là k = -5

Với n = -2 => m = (-2) . (-5) = 0

Với n = -1 => m = (-1) . (-5) = 5

Với n = 0 => m = 0 . (-5) = 0

Với n = 2 => m = 2 . (-5) = -10

Hoàn thành bảng số liệu:

n	-2	-1	0	1	2
m	10	5	0	-5	-10

Bài 4 trang 14 SGK Toán 7 tập 1

Cho biết hai đại lượng S và t tỉ lệ thuận với nhau:

S	1	2	3	4	5
t	-3	?	?	?	?

a) Tính các giá trị chưa biết trong bảng trên.

b) Viết công thức tính t theo S.

Hướng dẫn giải:

a) Với S = 1; t = -3 => $\frac{t}{S} = \frac{{ - 3}}{1} = - 3$ $\frac{t}{S} = \frac{{ - 3}}{1} = - 3$

Hai đại lượng S và t tỉ lệ thuận với nhau

Vậy hệ số tỉ lệ k = -3

Với S = 2 => t = 2.(-3) = -6

Với S = 3 => t = 3. (-3) = -9

Với S = 4 => t = 4.(-3) = -12

Với S = 5 => t = 5.(-3) = -15

Hoàn thành bảng số liệu:

S	1	2	3	4	5
t	-3	-6	-9	-12	-15

b) Hệ số tỉ lệ của t đối với S là: k = (-3) : 1 = -3

Vậy ta có: t = (-3).S

Bài 5 trang 14 SGK Toán 7 tập 1

Trong các trường hợp sau hãy kiểm tra xem đại lượng x có tỉ lệ thuận với đại lượng y hay không.

a)

x	2	4	6	-8
y	1,2	2,4	3,6	-4,8

b)

x	1	2	3	4	5
y	3	6	9	12	25

Hướng dẫn giải:

a) Ta có: $\frac{1,2}{2}=\frac{2,4}{4}=\frac{3,6}{6}=\frac{-4,8}{-8}$ $\frac{1,2}{2}=\frac{2,4}{4}=\frac{3,6}{6}=\frac{-4,8}{-8}$ nên x và y tỉ lệ thuận với nhau.

b) Ta có: $\frac{3}{1}=\frac{6}{2}=\frac{9}{3}=\frac{12}{4}\neq \frac{25}{5}$ $\frac{3}{1}=\frac{6}{2}=\frac{9}{3}=\frac{12}{4}\neq \frac{25}{5}$ nên x và y không tỉ lệ thuận với nhau.

Bài 6 trang 15 SGK Toán 7 tập 1

Hai chiếc nhẫn bằng kim loại đồng chất có thể tích là 3 $cm^{3}$ và 2 $cm^{3}$ mỗi chiếc nặng bao nhiêu gam biết rằng hai chiếc nhẫn nặng 96,5 g? (Cho biết khối lượng và thể tích là hai đại lượng tỉ lệ thuận với nhau.)

Hướng dẫn giải:

Gọi khối lượng 2 chiếc nhẫn lần lượt là a và b. $(a,b\neq 0)$ $(a,b\neq 0)$.

Theo đề bài ta có: khối lượng và thể tích tỉ lệ thuận với nhau nên: $\frac{a}{3}=\frac{b}{2}$ $\frac{a}{3}=\frac{b}{2}$, lại có: a + b = 96,5.

$\Rightarrow \frac{a}{3}=\frac{b}{2}=\frac{a+b}{3+2}=\frac{96,5}{5}=19,3$ $\Rightarrow \frac{a}{3}=\frac{b}{2}=\frac{a+b}{3+2}=\frac{96,5}{5}=19,3$

$\Rightarrow a = 19,3. 3 = 57,9; b = 19,3. 2 = 38,6$ $\Rightarrow a = 19,3. 3 = 57,9; b = 19,3. 2 = 38,6$.

Vậy khối lượng hai chiếc nhẫn lần lượt là: 57,9 g và 38,6 g.

Bài 7 trang 14 SGK Toán 7 tập 1

Bốn cuộn dây điện có cùng cùng cùng loại có tổng khối lượng là 26 kg.

a) Tính khối lượng từng cuộn biết cuộn thứ nhất nặng bằng $\frac{1}{2}$ $\frac{1}{2}$ cuộn thứ hai, bằng $\frac{1}{4}$ $\frac{1}{4}$ cuộn thứ ba và bằng $\frac{1}{6}$ $\frac{1}{6}$ cuộn thứ tư.

b) Biết cuộn thứ nhất dài 100 m. Hãy tính xem một mét dây điện nặng bao nhiêu gam.

Hướng dẫn giải:

a) Gọi khối lượng cuộn dây thứ nhất, thứ hai, thứ ba và thứ tư lần lượt là: a, b, c, d. (a, b, c, d > 0).

Theo đề bài có: $a = \frac{1}{2}b = \frac{1}{4}c = \frac{1}{6}d$ $a = \frac{1}{2}b = \frac{1}{4}c = \frac{1}{6}d$

$\Rightarrow \frac{a}{1}=\frac{b}{2}=\frac{c}{4}=\frac{d}{6}=\frac{a+b+c+d}{1+2+4+6}=\frac{26}{13}=2$ $\Rightarrow \frac{a}{1}=\frac{b}{2}=\frac{c}{4}=\frac{d}{6}=\frac{a+b+c+d}{1+2+4+6}=\frac{26}{13}=2$

$\Rightarrow a = 2; b = 2. 2 = 4; c = 2. 4 = 8; d = 2. 6 = 12$ $\Rightarrow a = 2; b = 2. 2 = 4; c = 2. 4 = 8; d = 2. 6 = 12$

Vậy khối lượng các cuộn dây thứ nhất, thứ hai, thứ ba, thứ tư lần lượt là: 2 kg; 4kg; 8 kg và 12 kg.

b) Cuộn dây thứ nhất nặng 2 kg tương ứng dài 100m. Nên một mét dây điện nặng: 2 : 100 = 0,02 kg = 20 g.

Bài 8 trang 14 SGK Toán 7 tập 1

Một tam giác có 3 cạnh tỉ lệ với 3, 4, 5 và có chu vi là 60 cm. Tính độ dài các cạnh của tam giác đó.

Hướng dẫn giải:

Gọi độ dài 3 cạnh của tam giác lần lượt là: a, b, c. (a,b,c > 0).

Theo đề bài có: a + b + c = 60 và $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$ $\frac{a}{3}=\frac{b}{4}=\frac{c}{5}$.

$\Rightarrow \frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5$ $\Rightarrow \frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5$.

$\Rightarrow a = 5. 3 =15; b = 5.4 = 20; c = 5.5 = 25$ $\Rightarrow a = 5. 3 =15; b = 5.4 = 20; c = 5.5 = 25$.

Vậy độ dài ba cạnh của tam giác là: 15 cm, 20 cm, 25 cm.

Bài 9 trang 14 SGK Toán 7 tập 1

Tiến, Hùng và Mạnh cùng đi câu cá trong dịp hè. Tiến câu được 12 con, Hùng câu được 8 con và Mạnh câu được 10 con. Số tiền bán cá thu được tổng cộng 180 nghìn đồng. Hỏi nếu đem số tiền trên chia cho các bạn theo tỉ lệ với số con cá từng người câu được thì mỗi bạn nhận được bao nhiêu tiền?

.....................

Ngoài Giải Toán 7 Bài 2: Đại lượng tỉ lệ thuận, mời các bạn tham khảo các tài liệu lớp 7 khác trên VnDoc và các Đề thi giữa kì 2 lớp 7, Đề thi học kì 2 lớp 7 để có sự chuẩn bị cho các kì thi sắp tới đạt kết quả cao.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau đây:

Nhóm Tài liệu học tập lớp 7

Nhóm Sách Chân trời sáng tạo THCS

Bài tiếp theo: Giải Toán 7 bài 3: Đại lượng tỉ lệ nghịch