Toán 7 Bài 8: Tính chất ba đường cao của tam giác

Giải Toán 7 Bài 8: Tính chất ba đường cao của tam giác hướng dẫn giải bài tập trong SGK Toán 7 Chân trời sáng tạo tập 2, giúp các bạn học sinh củng cố kiến thức, rèn luyện kỹ năng giải môn Toán lớp 7 hiệu quả. Mời các bạn tham khảo.

Khởi động trang 77 Toán 7 Tập 2:

Làm thế nào để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của một tam giác?

Hướng dẫn giải

Khoảng cách từ mỗi đỉnh đến cạnh đối diện của tam giác là độ dài đường cao xuất phát từ đỉnh đến cạnh đối diện của đỉnh đó.

Khám phá 1 trang 77 Toán 7 tập 2 CTST

Em hãy vẽ một tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B đến cạnh đối diện AC của tam giác.

Hướng dẫn giải

Ta thực hiện theo các bước sau:

Bước 1. Vẽ tam giác ABC.

Bước 2. Đặt êke sao cho một cạnh của êke trùng với cạnh AC, di chuyển êke sao cho cạnh còn lại đi qua đỉnh B.

Bước 3. Khi đó kẻ một đoạn thẳng từ B đến cạnh AC thông qua cạnh của êke vừa đặt ở bước 2 ta thu được đoạn thẳng vuông góc từ đỉnh B đến cạnh AC.

Ta có hình vẽ sau:

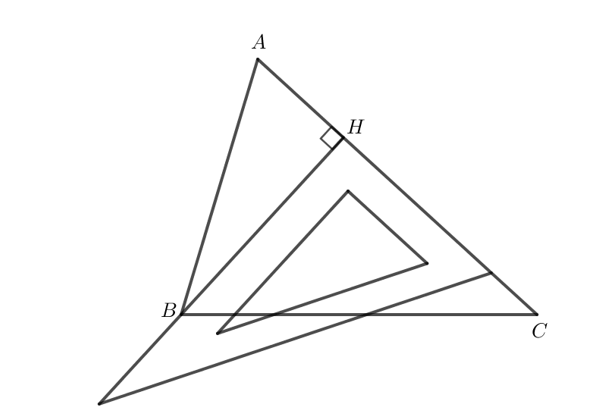
Thực hành 1 trang 77 Toán 7 tập 2 CTST

Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC.

Hướng dẫn giải

Để vẽ đường cao AH của tam giác nhọn ABC ta làm như sau:

Bước 1. Vẽ tam giác nhọn ABC.

Bước 2. Đặt êke sao cho 1 cạnh của êke trùng với cạnh BC, cạnh còn lại đi qua đỉnh A.

Khi đó kẻ 1 đường thẳng từ A đến BC thông qua cạnh đi đỉnh A vừa đặt, ta thu được đường cao đi qua đỉnh A. Đường thẳng này cắt cạnh BC tại một điểm, điểm này chính là điểm H.

Thực hiện tương tự đối với các đường cao BK và CE ta thu được hình vẽ sau:

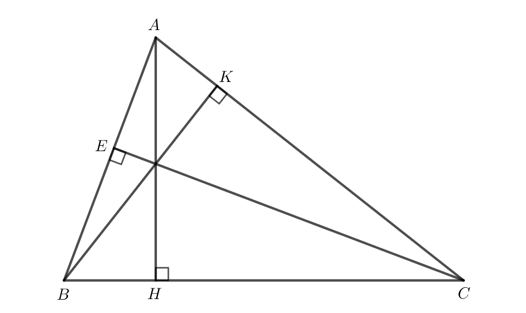
Vận dụng 1 trang 77 Toán 7 tập 2 CTST

Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a).

Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).

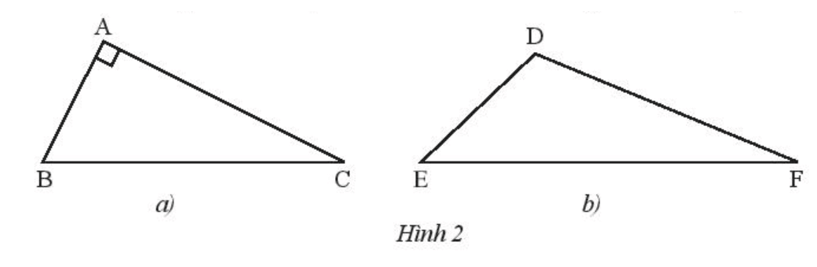Hướng dẫn giải

+) Hình 2a:

Tam giác ABC có góc BAC là góc vuông nên BA ⊥AC.

Do đó đường cao xuất phát từ đỉnh B của tam giác vuông ABC là BA.

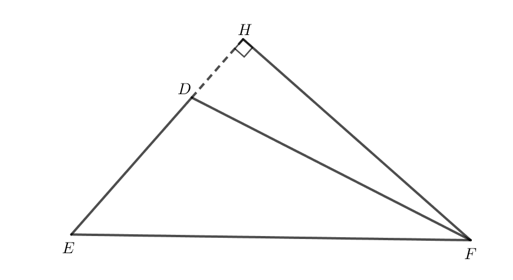
+) Hình 2b:

Tam giác DEF có góc EDF là góc tù nên đường cao xuất phát từ đỉnh F của tam giác DEF nằm ngoài tam giác.

Ta thực hiện theo các bước sau:

Bước 1. Vẽ tam giác tù DEF.

Bước 2. Kéo dài cạnh DE về phía D.

Bước 3. Đặt êke sao cho một cạnh của êke trùng với đường thẳng DE, di chuyển êke sao cho đỉnh còn lại đi qua đỉnh F.

Bước 4. Khi đó kẻ một đoạn thẳng từ F đến cạnh DE thông qua cạnh của êke vừa đặt ở bước 2 ta thu được đoạn thẳng vuông góc từ đỉnh F đến cạnh DE.

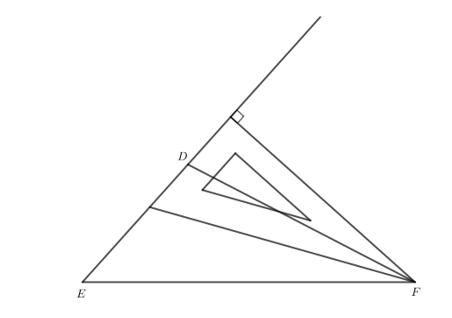
Bước 5. Thực hiện đánh dấu chân đường vuông góc từ F đến DE và xóa các đoạn thừa, ta thu được đường cao FH của tam giác DEF như sau:

Khám phá 2 trang 77 Toán 7 tập 2 CTST

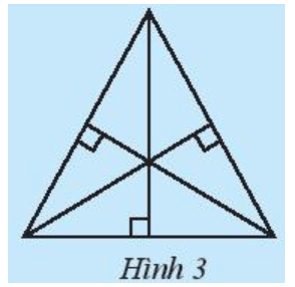
Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). Em hãy quan sát và cho biết các đường cao vừa vẽ có cùng đi qua một điểm hay không.

Hướng dẫn giải

Bước 1. Thực hiện đặt êke sao cho 1 cạnh của êke trùng với 1 cạnh của tam giác, cạnh còn lại đi qua đỉnh đối diện với cạnh đó. Khi đó ta thu được 1 đường cao của tam giác.

Bước 2. Thực hiện tương tự với 2 đỉnh còn lại, ta thu được 3 đường cao của tam giác.

Khi đó ta thấy ba đường cao vừa vẽ cùng đi qua một điểm.

Thực hành 2 trang 78 Toán 7 tập 2 CTST

Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6).

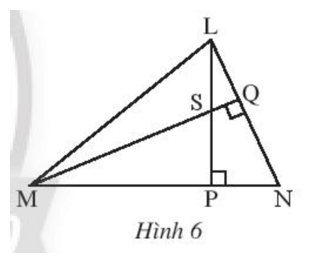
Chứng minh rằng NS vuông góc với ML.

Hướng dẫn giải

Tam giác LMN có hai đường cao LP và MQ cắt nhau tại S nên S là trực tâm của tam giác LMN.

Do đó NS vuông góc với ML.

Vận dụng 2 trang 78 Toán 7 tập 2 CTST

Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.

Hướng dẫn giải

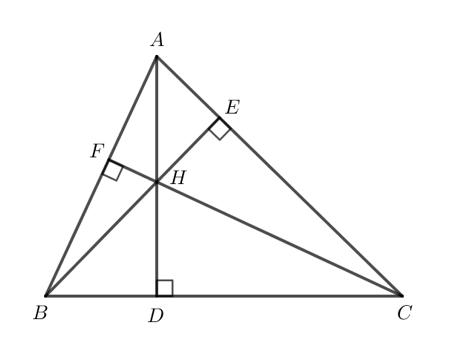
Tam giác HBC có HD ⊥BC, BF ⊥ HC nên HD và BF là hai đường cao của tam giác HBC.

Mà HD và BF cắt nhau tại A nên A là trực tâm của tam giác HBC.

Tam giác HAB có HF ⊥AB, BD ⊥ AH nên HF, BD là hai đường cao của tam giác HAB.

Mà HF và BD cắt nhau tại C nên C là trực tâm của tam giác HAB.

Tam giác HAC có HE ⊥AC, CD ⊥AH nên HE, CD là hai đường cao của tam giác HAC.

Mà HE và CD cắt nhau tại B nên B là trực tâm của tam giác HAC.

Bài 1 trang 78 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.

Hướng dẫn giải:

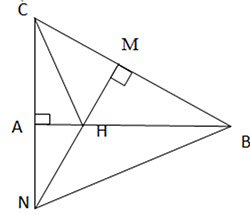
Xét tam giác CNB có:

BA ⊥ CA hay BA ⊥ CN => BA là đường cao của tam giác CNB

HM ⊥ CB hay NM ⊥ CB => NM là đường cao của tam giác CNB

NM giao với BA tại điểm H

=> H là trực tâm của tam giác CNB

=> CH ⊥ NB.

Bài 2 trang 78 Toán 7 tập 2 CTST

Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.

Hướng dẫn giải:

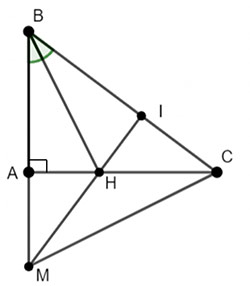
Gọi MH giao với BC tại điểm I.

+ Xét ∆MBH và ∆CBH có:

MB = MC

$\widehat{MBH}=\widehat{CBH}$

BH chung

=> ∆MBH = ∆CBH (c.g.c)

$=>\widehat{BMH}=\widehat{BCH}$

+ Xét tam giác ABC vuông tại A có: $\widehat{ABC}+\widehat{ACB}={90}^o$

+ Ta có: $\widehat{BMI}+\widehat{ABC}=\widehat{ACB}+\widehat{ABC}={90}^o$

+ Xét tam giác BMI có: $\widehat{BMI}+\widehat{ABC}={90}^o$

$=>\widehat{BIM}={90}^o$.

=> MI ⊥ BC hay MH vuông góc với BC.

Bài 3 trang 78 Toán 7 tập 2 CTST

Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:

a) DE vuông góc với BC.

b) BE vuông góc với DC.

Hướng dẫn giải:

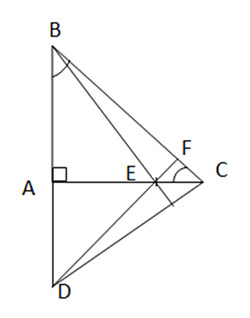
a) Gọi F là giao điểm của DE và BC

+ AD = AE => ∆ADE cân tại A

∆ABC vuông cân tại A => BA ⊥ AC hay EA ⊥ AD

=> ∆ ADE vuông cân tại A

$=>\widehat{AED}=\widehat{ADE}=45°$

+ ∆ ABC vuông cân tại A

$=>\widehat{ABC}=\widehat{ACB}=45°$

+ Xét ∆EFC có: $\widehat{FEC}+\widehat{FCE}+\widehat{EFC}=180°$

$=>45°+45°+\widehat{EFC}=180°$

$=>\widehat{EFC}=180°-90°=90°$

=> EF ⊥ BC hay DE ⊥ BC.

b) Xét tam giác BCD có: CA ⊥ BD => CA là đường cao của ∆ BCD

DE ⊥ BC => DE là đường cao của ∆ BCD

Mà DE giao với CA tại E

=> E là trực tâm của ∆ BCD

=> BE ⊥ CD.

Bài 4 trang 78 Toán 7 tập 2 CTST

Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.

Hướng dẫn giải:

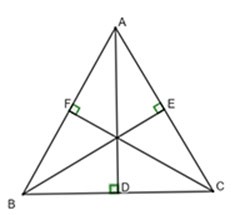
BE là đường cao của $∆ABC\Rightarrow ∆ABE$ vuông tại E.

CF là đường cao của $∆ABC\Rightarrow ∆AFC$ vuông tại F.

AD là đường cao của $∆ABC\Rightarrow ∆ADC$ vuông tại D.

+ Xét ∆ ABE vuông tại E và ∆ AFC vuông tại F có:

BE = CF

$\widehat{EAF}$ chung

$\Rightarrow ∆ABE=∆AFC$ (góc nhọn và một cạnh góc vuông).

$\Rightarrow AB=AC(1)$

+ Xét ∆CDA vuông tại D và ∆ AFC vuông tại F có:

AC chung

AD = CF

$\Rightarrow ∆CDA=∆AFC$ (cạnh huyền và một cạnh góc vuông).

$\Rightarrow \widehat{CAF}=\widehat{ACD}$

$\Rightarrow ∆ABC$ cân tại B

=> AB = BC (2)

Từ (1), (2) ta có: AB = AC = BC

$\Rightarrow ∆ABC$ đều.