Giải Toán 7 bài 5 Lũy thừa của một số hữu tỉ

Giải SGK Toán 7 trang 19, 20

Giải bài tập Toán 7 trang 19, 20: Lũy thừa của một số hữu tỉ

A. Tóm tắt lý thuyết Lũy thừa của một số hữu tỉ
B. Giải Toán 7 trang 19, 20 Lũy thừa của một số hữu tỉ

Giải bài tập trang 19, 20 SGK Toán 7 tập 1: Lũy thừa của một số hữu tỉ tổng hợp lý thuyết, câu hỏi và lời giải cho các câu hỏi trong SGK Toán 7 bài 5 phần Đại số. Các đáp án được trình bày chi tiết rõ ràng, giúp các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 7 hiệu quả.

A. Tóm tắt lý thuyết Lũy thừa của một số hữu tỉ

Lũy thừa với số mũ tự nhiên

Lũy thừa bậc n (n là số tự nhiên lớn hơn 1) của một số hữu tỉ x là tích của n thừa số bằng x

Bài tập môn Toán lớp 7

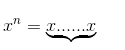
n thừa số (x ∈ Q, n ∈ N, n> 1)

Nếu x = a/b thì

xⁿ =(a/b)ⁿ = aⁿ/bⁿ

Quy ước a^o = 1 (a ∈ N*)

x^o = 1 (x ∈ Q, x ≠ 0)

Tích của hai lũy thưa cùng cơ số

x^m. xⁿ= x+m^x+n (x ∈ Q, n∈ N)

Thương của hai lũy thừa cùng cơ số khác 0

x^_m : xⁿ= x + m^x-n (x ≠ 0, m ≥ n)

Lũy thừa của lũy thừa

(x^m)ⁿ = x^m.n

B. Giải Toán 7 trang 19, 20 Lũy thừa của một số hữu tỉ

Bài 27 trang 19 SGK Toán 7 Tập 1

Tính:

$\left(\dfrac{-1}{3} \right)^4 ; \left(-2\dfrac{1}{4} \right)^3 ; (-0,2)^2; (-5,3)^o.$ ${(\frac{- 1}{3})}^{4}; {(- 2 \frac{1}{4})}^{3}; (- 0, 2)^{2}; (- 5, 3)^{o} .$

Đáp án và hướng dẫn giải

Ta có:

$+) \left(\dfrac{-1}{3} \right)^4 = \left(\dfrac{-1}{3} \right) . \left(\dfrac{-1}{3} \right) . \left(\dfrac{-1}{3} \right). \left(\dfrac{-1}{3} \right) = \dfrac{1}{81}$ $+) {(\frac{- 1}{3})}^{4} = (\frac{- 1}{3}) . (\frac{- 1}{3}) . (\frac{- 1}{3}) . (\frac{- 1}{3}) = \frac{1}{81}$

$+) \left(-2\dfrac{1}{4} \right)^3 = \left(\dfrac{-9}{4} \right)^3 = \left(\dfrac{-9}{4} \right).\left(\dfrac{-9}{4} \right).\left(\dfrac{-9}{4} \right) = \dfrac{-729}{64}$ $+) {(- 2 \frac{1}{4})}^{3} = {(\frac{- 9}{4})}^{3} = (\frac{- 9}{4}) . (\frac{- 9}{4}) . (\frac{- 9}{4}) = \frac{- 729}{64}$

$+) (- 0, 2)^{2} = (- 0, 2) . (- 0, 2) = 0, 04$

$+) (- 5, 3)^{o} = 1$

Bài 28 trang 19 SGK Toán 7 Tập 1

Tính:

$\left(\dfrac{-1}{2} \right)^2; \left(\dfrac{-1}{2} \right)^3; \left(\dfrac{-1}{2} \right)^4; \left(\dfrac{-1}{2} \right)^5$ ${(\frac{- 1}{2})}^{2}; {(\frac{- 1}{2})}^{3}; {(\frac{- 1}{2})}^{4}; {(\frac{- 1}{2})}^{5}$

Hãy rút ra nhận xét về dấu của lũy thừa với số mũ chẵn và lũy thừa với số mũ lẻ của một số hữu tỉ âm.

Đáp án và hướng dẫn giải

Ta có:

+) $\left(\dfrac{-1}{2} \right)^2 = \left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right) = \dfrac{1}{4}$ ${(\frac{- 1}{2})}^{2} = (\frac{- 1}{2}) . (\frac{- 1}{2}) = \frac{1}{4}$

+) $\left(\dfrac{-1}{2} \right)^3 = \left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right) = \dfrac{-1}{8}$ ${(\frac{- 1}{2})}^{3} = (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) = \frac{- 1}{8}$

+) $\left(\dfrac{-1}{2} \right)^4 = \left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right) = \dfrac{1}{16}$ ${(\frac{- 1}{2})}^{4} = (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) = \frac{1}{16}$

+) $\left(\dfrac{-1}{2} \right)^5 = \left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right).\left(\dfrac{-1}{2} \right) = \dfrac{-1}{32}$ ${(\frac{- 1}{2})}^{5} = (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) . (\frac{- 1}{2}) = \frac{- 1}{32}$

Nhận xét:

+ Lũy thừa bậc chẵn (số mũ chẵn) của một số hữu tỉ âm là một số dương.

+ Lũy thừa bậc lẻ (số mũ lẻ) của một số hữu tỉ âm là một số âm

Bài 29 trang 19 SGK Toán 7 Tập 1

Viết số $\dfrac{16}{81}$ $\frac{16}{81}$ dưới dạng một lũy thừa, ví dụ $\dfrac{16}{81} = \left(\dfrac{4}{9} \right)^2.$ $\frac{16}{81} = {(\frac{4}{9})}^{2} .$ Hãy tìm các cách viết khác.

Đáp án và hướng dẫn giải

Ta có:

$\dfrac{16}{81} = \left(\dfrac{4}{9} \right)^2 = \left(\dfrac{2^2}{3^2} \right)^2 = \left[\left(\dfrac{2}{3} \right)^2\right]^2$ $\frac{16}{81} = {(\frac{4}{9})}^{2} = {(\frac{2^{2}}{3^{2}})}^{2} = {[{(\frac{2}{3})}^{2}]}^{2}$

Lưu ý: $x^n = \underbrace{x.x.x.x. ... .x}_{n \, \text{thừa số}} \,\, (x \in \mathbb{Q}, \, n \in \mathbb{N}, \, n > 1)$ $x^{n} = \underset{n thừa số}{\underset{⏟}{x . x . x . x . . . . . x}} (x \in Q, n \in N, n > 1)$

Bài 30 trang 19 SGK Toán 7 Tập 1

Tìm x, biết:

a) $x : \left(-\dfrac{1}{2} \right)^3 = -\dfrac{1}{2};$ $x : {(- \frac{1}{2})}^{3} = - \frac{1}{2};$

b) $\left(\dfrac{3}{4} \right)^5 . x = \left(\dfrac{3}{4} \right)^7$ ${(\frac{3}{4})}^{5} . x = {(\frac{3}{4})}^{7}$

Đáp án và hướng dẫn giải

a) $x : \left(-\dfrac{1}{2} \right)^3 = -\dfrac{1}{2}$ $x : {(- \frac{1}{2})}^{3} = - \frac{1}{2}$

$\Leftrightarrow x = \left(-\dfrac{1}{2} \right).\left(-\dfrac{1}{2} \right)^3$ $\Leftrightarrow x = (- \frac{1}{2}) . {(- \frac{1}{2})}^{3}$

$\Leftrightarrow x = \left(-\dfrac{1}{2} \right)^4 = \dfrac{1}{16}$ $\Leftrightarrow x = {(- \frac{1}{2})}^{4} = \frac{1}{16}$

b) $\left(\dfrac{3}{4} \right)^5 . x = \left(\dfrac{3}{4} \right)^7$ ${(\frac{3}{4})}^{5} . x = {(\frac{3}{4})}^{7}$

$\Leftrightarrow x = \left(\dfrac{3}{4} \right)^7 : \left(\dfrac{3}{4} \right)^5$ $\Leftrightarrow x = {(\frac{3}{4})}^{7} : {(\frac{3}{4})}^{5}$

$\Leftrightarrow x = \left(\dfrac{3}{4} \right)^2 =\dfrac{9}{16}$ $\Leftrightarrow x = {(\frac{3}{4})}^{2} = \frac{9}{16}$

Lưu ý:

$+ \,\,\,\, a^m : a^n = a^{m - n};\,\,a \ne 0, \, m \geq 0\\$ $+ a^{m} : a^{n} = a^{m - n}; a \neq 0, m \geq 0$

$+ \,\,\,\, a^m.a^n = a^{m + n}$ $+ a^{m} . a^{n} = a^{m + n}$

Bài 31 SGK Toán 7 tập 1 trang 19

Viết các số (0,25)⁸ và (0,125)⁴ dưới dạng các lũy thừa với cơ số 0,5.

Đáp án và hướng dẫn giải

Ta có:

(0,25)⁸ = [(0,5)2]⁸ = 0,5¹⁶

(0,125)⁴ = [(0,5)³]⁴ = 0,5¹²

Bài 32 trang 19 SGK Toán 7 Tập 1

Đố: Hãy chọn hai chữ số sao cho có thể viết hai chữ đó thành một lũy thừa để được kết quả là số nguyên dương nhỏ nhất. (Chọn được càng nhiều càng tốt).

Đáp án và hướng dẫn giải

Ta có số nguyên dương nhỏ nhất là 1 nên:

1¹ = 1² = 1³ = 1⁴ = 1⁵ = 1⁶ = 1⁷ = 1⁸ = 1⁹ = 1

1⁰ = 2⁰ = 3⁰ = 4⁰ = 5⁰ = 6⁰ = 7⁰ = 8⁰ = 9⁰ = 1

Bài 33 trang 20 SGK Toán 7 Tập 1

Dùng máy tính bỏ túi để tính:

(3,5)² ; (-0,12)³ ; (1,5)⁴ ; (-0,1)⁵ ; (1,2)⁶

Đáp án và hướng dẫn giải

Sử dụng máy tính và lần lượt thực hiện như sau:

(3,5)² = 12.25

(-0,12)³ = -0,001728

(1,5)⁴ = 5,0625

(-0,1)⁵ = -0,00001

(1,2)⁶ = 2,985984

..........................

Trên đây, VnDoc đã gửi tới các bạn Giải Toán 7 bài 5 Lũy thừa của một số hữu tỉ. Tài liệu thuộc chuyên mục Giải bài tập Toán 7 trên VnDoc với các hướng dẫn giải chi tiết cho các câu hỏi trong SGK Toán 7, hy vọng giúp các em biết vận dụng để làm các bài tập cơ bản và nâng cao, từ đó nâng cao kỹ năng giải Toán và đạt điểm cao trong các bài thi, bài kiểm tra định kỳ môn Toán lớp 7 sắp tới. Chúc các em học tốt.

Ngoài tài liệu trên, mời các bạn tham khảo thêm: Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... cũng được cập nhật liên tục trên VnDoc.com để học tốt môn Toán hơn.

Bài tiếp theo: Giải bài tập trang 22 SGK Toán lớp 7 tập 1: Lũy thừa của 1 số hữu tỉ (tiếp theo)

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

41

11.171

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Phương

Tải về

Chọn file muốn tải về:

Giải Toán 7 bài 5 Lũy thừa của một số hữu tỉ

169 KB

Tải file định dạng .Doc

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!