Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Giải Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Giải SKG Toán 7 bài 1

Bài trước

Tải về

Bài sau

Giải Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Giải Toán 7 bài 1: Tập hợp Q các số hữu tỉ 3 bộ sách Cánh Diều, Chân Trời Sáng Tạo, Kết Nối Tri Thức được biên soạn đầy đủ, chi tiết, sẽ giúp học sinh chuẩn bị bài ở nhà tốt hơn.

Mời các bạn tham khảo phần lời giải chi tiết 3 bộ sách mới theo chương trình GDPT, các bạn tìm lời giải của từng sách theo link bên dưới nhé:

A. Giải Toán 7 bài 1 sách Chân trời sáng tạo

Giải Toán 7 bài 1 Tập hợp các số hữu tỉ sách Chân trời sáng tạo bao gồm đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 1 chương trình sách mới, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 7 sách Chân trời sáng tạo một cách hiệu quả.

Mời các bạn tham khảo chi tiết tại đây: Toán 7 bài 1 Tập hợp các số hữu tỉ CTST

Bài 1 trang 9 SGK Toán 7 tập 1

Thay dấu ? bằng kí hiệu “∈” hoặc “ ∉” thích hợp:

Hướng dẫn giải:

$\begin{array}{l} - 7 \notin \mathbb{N};\,\,\,\,\,\,\, - 17 \in \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\, - 38 \in Q\\\frac{4}{5} \notin \mathbb{Z};\,\,\,\,\,\,\,\,\,\,\,\frac{4}{5} \in \mathbb{Q};\,\,\,\,\,\,\,\,\,\,\,\,\,\,0,25 \notin \mathbb{Z};\,\,\,\,\,3,25 \in Q\end{array}$ $\begin{array}{l} - 7 \notin N; - 17 \in Z; - 38 \in Q \\ \frac{4}{5} \notin Z; \frac{4}{5} \in Q; 0, 25 \notin Z; 3, 25 \in Q \end{array}$

Bài 2 trang 9 SGK Toán 7 tập 1

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{{ - 5}}{9}$ $\frac{- 5}{9}$ ?

$\frac{{ - 10}}{{18}};\frac{{10}}{{18}};\frac{{15}}{{ - 27}}; - \frac{{20}}{{36}};\frac{{ - 25}}{{27}}$ $\frac{- 10}{18}; \frac{10}{18}; \frac{15}{- 27}; - \frac{20}{36}; \frac{- 25}{27}$

b) Tìm số đối của mỗi số sau: $12;{\text{ }} - \frac{5}{9};{\text{ }} - 0,375;{\text{ }}0;{\text{ }}2\frac{2}{5}$ $12; - \frac{5}{9}; - 0, 375; 0; 2 \frac{2}{5}$

Hướng dẫn giải:

a) Ta có:

$\begin{matrix} \dfrac{{ - 10}}{{18}} = \dfrac{{ - 10:2}}{{18:2}} = \dfrac{{ - 5}}{9} \hfill \\ \dfrac{{10}}{{18}} = \dfrac{{10:2}}{{18:2}} = \dfrac{5}{9} \hfill \\ \dfrac{{15}}{{ - 27}} = \dfrac{{15:3}}{{ - 27:3}} = \dfrac{5}{{ - 9}} = \dfrac{{ - 5}}{9} \hfill \\ - \dfrac{{20}}{{36}} = \dfrac{{ - 20:4}}{{36:4}} = \dfrac{{ - 5}}{9} \hfill \\ \end{matrix}$ $\begin{matrix} \frac{- 10}{18} = \frac{- 10 : 2}{18 : 2} = \frac{- 5}{9} \\ \frac{10}{18} = \frac{10 : 2}{18 : 2} = \frac{5}{9} \\ \frac{15}{- 27} = \frac{15 : 3}{- 27 : 3} = \frac{5}{- 9} = \frac{- 5}{9} \\ - \frac{20}{36} = \frac{- 20 : 4}{36 : 4} = \frac{- 5}{9} \end{matrix}$

Vậy những phân số nào biểu diễn số hữu tỉ $\frac{{ - 5}}{9}$ $\frac{- 5}{9}$ là $\frac{{ - 10}}{{18}};\frac{{15}}{{ - 27}}; - \frac{{20}}{{36}}$ $\frac{- 10}{18}; \frac{15}{- 27}; - \frac{20}{36}$

b) Số đối của số hữu tỉ 12 là số -12

Số đối của số hữu tỉ $\frac{{ - 5}}{9}$ $\frac{- 5}{9}$ là số $\frac{5}{9}$ $\frac{5}{9}$

Số đối của số hữu tỉ -0,375 là số 0,375

Số đối của số hữu tỉ 0 là số 0

Ta có: $2\frac{2}{5} = \frac{{12}}{5}$ $2 \frac{2}{5} = \frac{12}{5}$

Số đối của số hữu tỉ $2\frac{2}{5}$ $2 \frac{2}{5}$ là số $- \frac{{12}}{5}$ $- \frac{12}{5}$

Bài 3 trang 9 SGK Toán 7 tập 1

a) Các điểm A; B; C trong Hình 8 biểu diễn số hữu tỉ nào?

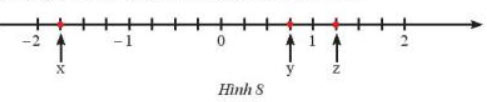
Hình 8

b) Biểu diễn các số hữu tỉ $\frac{{ - 2}}{5};1\frac{1}{5};\frac{3}{5}; - 0,8$ $\frac{- 2}{5}; 1 \frac{1}{5}; \frac{3}{5}; - 0, 8$ trên trục số.

Hướng dẫn giải:

a) - Đoạn thẳng đơn vị chia thành 4 đoạn thẳng bằng nhau, đơn vị mới bằng $\frac{1}{4}$ $\frac{1}{4}$ đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm y nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm y biểu diễn số hữu tỉ: $\frac{3}{4}$ $\frac{3}{4}$

+ Điểm z nằm cách O một đoạn bằng 5 đơn vị mới

=> Điểm z biểu diễn số hữu tỉ: $\frac{5}{4}$ $\frac{5}{4}$

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm x nằm cách O một đoạn bằng 7 đơn vị mới.

=> Điểm x biểu diễn số hữu tỉ: $\frac{{ - 7}}{4}$ $\frac{- 7}{4}$

b) Ta có: $1\frac{1}{5} = \frac{6}{5}; - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}$ $1 \frac{1}{5} = \frac{6}{5}; - 0, 8 = \frac{- 8}{10} = \frac{- 4}{5}$

Biểu diễn các số hữu tỉ như sau:

Biểu diễn các số hữu tỉ

Bài 4 trang 10 SGK Toán 7 tập 1

a) Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm?

$\frac{5}{{12}}; - \frac{4}{5};2\frac{2}{3}; - 2;\frac{0}{{234}}; - 0,32$ $\frac{5}{12}; - \frac{4}{5}; 2 \frac{2}{3}; - 2; \frac{0}{234}; - 0, 32$

b) Hãy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn.

Hướng dẫn giải:

a) Ta có:

$\begin{matrix} \dfrac{5}{{12}} > 0 \hfill \\ - \dfrac{4}{5} < 0 \hfill \\ 2\dfrac{2}{3} > 0 \hfill \\ - 2 < 0 \hfill \\ \dfrac{0}{{234}} = 0 \hfill \\ - 0,32 < 0 \hfill \\ \end{matrix}$ $\begin{matrix} \frac{5}{12} > 0 \\ - \frac{4}{5} < 0 \\ 2 \frac{2}{3} > 0 \\ - 2 < 0 \\ \frac{0}{234} = 0 \\ - 0, 32 < 0 \end{matrix}$

Các số hữu tỉ dương là: $\frac{5}{{12}};2\frac{2}{3}$ $\frac{5}{12}; 2 \frac{2}{3}$

Các số hữu tỉ âm là: $- \frac{4}{5}; - 2; - 0,32$ $- \frac{4}{5}; - 2; - 0, 32$

Số $\frac{0}{{234}}$ $\frac{0}{234}$ không là số hữu tỉ dương cũng không là số hữu tỉ âm.

b) Thực hiện so sánh các nhóm số đã phân loại ở câu a

Nhóm các số hữu tỉ dương là: $\frac{5}{{12}};2\frac{2}{3}$ $\frac{5}{12}; 2 \frac{2}{3}$

Ta có: $2\frac{2}{3} = \frac{8}{3} = \frac{{32}}{{12}}$ $2 \frac{2}{3} = \frac{8}{3} = \frac{32}{12}$

$\frac{5}{{12}} < \frac{{32}}{{12}} \Rightarrow \frac{5}{{12}} < 2\frac{2}{3}$ $\frac{5}{12} < \frac{32}{12} \Rightarrow \frac{5}{12} < 2 \frac{2}{3}$

Nhóm các số hữu tỉ âm là: $- \frac{4}{5}; - 2; - 0,32$ $- \frac{4}{5}; - 2; - 0, 32$

Ta có:

$\begin{matrix} - 0,32 = \dfrac{{ - 32}}{{100}} = \dfrac{{ - 8}}{{25}} \hfill \\ - \dfrac{4}{5} = \dfrac{{ - 20}}{{25}} \hfill \\ - 2 = \dfrac{{ - 50}}{{25}} \hfill \\ \end{matrix}$ $\begin{matrix} - 0, 32 = \frac{- 32}{100} = \frac{- 8}{25} \\ - \frac{4}{5} = \frac{- 20}{25} \\ - 2 = \frac{- 50}{25} \end{matrix}$

=> $\frac{{ - 50}}{{25}} < \frac{{ - 20}}{{25}} < \frac{{ - 8}}{{25}}$ $\frac{- 50}{25} < \frac{- 20}{25} < \frac{- 8}{25}$

=> $- 2 < - \frac{4}{5} < - 0,32$ $- 2 < - \frac{4}{5} < - 0, 32$

Vì số hữu tỉ âm luôn nhỏ hơn 0 và nhỏ hơn số hữu tỉ dương nên ta có:

$- 2 < - \frac{4}{5} < - 0,32 < \frac{0}{{234}} < \frac{5}{{12}} < 2\frac{2}{3}$ $- 2 < - \frac{4}{5} < - 0, 32 < \frac{0}{234} < \frac{5}{12} < 2 \frac{2}{3}$

Vậy sắp xếp các số trên theo thứ tự từ nhỏ đến lớn như sau:

$- 2; - \frac{4}{5}; - 0,32;\frac{0}{{234}};\frac{5}{{12}};2\frac{2}{3}$ $- 2; - \frac{4}{5}; - 0, 32; \frac{0}{234}; \frac{5}{12}; 2 \frac{2}{3}$

Bài 5 trang 10 SGK Toán 7 tập 1

So sánh các cặp số hữu tỉ sau:

a) $\frac{2}{{ - 5}}$ $\frac{2}{- 5}$ và $\frac{{ - 3}}{8}$ $\frac{- 3}{8}$

c) $\frac{{ - 137}}{{200}}$ $\frac{- 137}{200}$ và $\frac{{37}}{{ - 25}}$ $\frac{37}{- 25}$

b) -0,85 và $\frac{{ - 17}}{{20}}$ $\frac{- 17}{20}$

d) $- 1\frac{3}{{10}}$ $- 1 \frac{3}{10}$ và $- \left( {\frac{{ - 13}}{{ - 10}}} \right)$ $- (\frac{- 13}{- 10})$

Hướng dẫn giải:

a) $\frac{2}{{ - 5}}$ $\frac{2}{- 5}$ và $\frac{{ - 3}}{8}$ $\frac{- 3}{8}$

Ta có:

$\begin{matrix} \dfrac{2}{{ - 5}} = \dfrac{{2.8}}{{ - 5.8}} = \dfrac{{16}}{{ - 40}} = \dfrac{{ - 16}}{{40}} \hfill \\ \dfrac{{ - 3}}{8} = \dfrac{{ - 3.5}}{{8.5}} = \dfrac{{ - 15}}{{40}} \hfill \\ \end{matrix}$ $\begin{matrix} \frac{2}{- 5} = \frac{2.8}{- 5.8} = \frac{16}{- 40} = \frac{- 16}{40} \\ \frac{- 3}{8} = \frac{- 3.5}{8.5} = \frac{- 15}{40} \end{matrix}$

Vì -16 < -15 => $\frac{{ - 16}}{{40}} < \frac{{ - 15}}{{40}}$ $\frac{- 16}{40} < \frac{- 15}{40}$

=> $\frac{2}{{ - 5}} < \frac{{ - 3}}{8}$ $\frac{2}{- 5} < \frac{- 3}{8}$

b) -0,85 và $\frac{{ - 17}}{{20}}$ $\frac{- 17}{20}$

Ta có:

$- 0,85 = \frac{{ - 85}}{{100}} = \frac{{ - 85:5}}{{100:5}} = \frac{{ - 17}}{{20}}$ $- 0, 85 = \frac{- 85}{100} = \frac{- 85 : 5}{100 : 5} = \frac{- 17}{20}$

=> $- 0,85 = \frac{{ - 17}}{{20}}$ $- 0, 85 = \frac{- 17}{20}$

c) $\frac{{ - 137}}{{200}}$ $\frac{- 137}{200}$ và $\frac{{37}}{{ - 25}}$ $\frac{37}{- 25}$

Ta có:

$\frac{{37}}{{ - 25}} = \frac{{37.8}}{{ - 25.8}} = \frac{{296}}{{ - 200}} = \frac{{ - 296}}{{200}}$ $\frac{37}{- 25} = \frac{37.8}{- 25.8} = \frac{296}{- 200} = \frac{- 296}{200}$

Vì -137 > -296 => $\frac{{ - 137}}{{200}} > \frac{{ - 296}}{{200}}$ $\frac{- 137}{200} > \frac{- 296}{200}$

=> $\frac{{ - 137}}{{200}} > \frac{{37}}{{ - 25}}$ $\frac{- 137}{200} > \frac{37}{- 25}$

d) $- 1\frac{3}{{10}}$ $- 1 \frac{3}{10}$ và $- \left( {\frac{{ - 13}}{{ - 10}}} \right)$ $- (\frac{- 13}{- 10})$

Ta có:

$- 1\frac{3}{{10}} = \frac{{ - 13}}{{10}}$ $- 1 \frac{3}{10} = \frac{- 13}{10}$

$- \left( {\frac{{ - 13}}{{ - 10}}} \right) = - \left( {\frac{{13}}{{10}}} \right) = - \frac{{13}}{{10}}$ $- (\frac{- 13}{- 10}) = - (\frac{13}{10}) = - \frac{13}{10}$

=> $- 1\frac{3}{{10}} = - \left( {\frac{{ - 13}}{{ - 10}}} \right)$ $- 1 \frac{3}{10} = - (\frac{- 13}{- 10})$

B. Giải Toán 7 bài 1 sách Kết nối tri thức

Toán 7 bài 1 Tập hợp các số hữu tỉ Kết nối tri thức bao gồm đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 1 chương trình sách mới, giúp các em học sinh ôn tập, củng cố kiến thức, luyện tập Giải Toán 7 sách Kết nối tri thức với cuộc sống một cách hiệu quả.

Mời bạn tham khảo chi tiết tại đây: Giải Toán 7 bài 1 Tập hợp các số hữu tỉ KNTT

Bài 1.1 SGK Toán 7 tập 1 trang 9

Khẳng định nào sau đây là đúng?

$a)0,25 \in \mathbb{Q};b) - \frac{6}{7} \in \mathbb{Q};c) - 235 \notin \mathbb{Q}$ $a) 0, 25 \in Q; b) - \frac{6}{7} \in Q; c) - 235 \notin Q$

Hướng dẫn giải

a) Đúng vì $0,25{\rm{ }} = \frac{{25}}{{100}} = \frac{1}{4}$ $0, 25 = \frac{25}{100} = \frac{1}{4}$ là số hữu tỉ

b) Đúng vì $\frac{{ - 6}}{7}$ $\frac{- 6}{7}$ là số hữu tỉ

c) Sai vì $- 235 = \frac{{ - 235}}{1}$ $- 235 = \frac{- 235}{1}$ là số hữu tỉ.

Chú ý: Một số nguyên cũng là một số hữu tỉ.

Bài 1.2 SGK Toán 7 tập 1 trang 9

Tìm số đối của các số hữu tỉ sau:

a) -0,75

b) $6\frac{1}{5}$ $6 \frac{1}{5}$

Hướng dẫn giải:

a) Số đối của số hữu tỉ -0,75 là –(-0,75) = 0,75

b) Số đối của số hữu tỉ $6\frac{1}{5}$ $6 \frac{1}{5}$ là $- 6\frac{1}{5}$ $- 6 \frac{1}{5}$

Bài 1.3 SGK Toán 7 tập 1 trang 9

Các điểm A, B, C, D (H.17) biểu diễn những số hữu tỉ nào?

Các điểm A, B, C, D (H.1.7) biểu diễn những số hữu tỉ nào

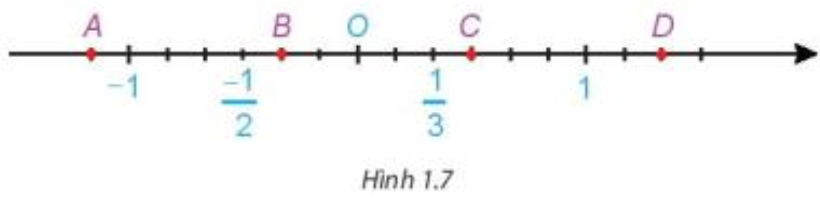
Hướng dẫn giải:

- Đoạn thẳng đơn vị chia thành 6 đoạn thẳng bằng nhau, đơn vị mới bằng $\frac{1}{6}$ $\frac{1}{6}$ đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm C nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm C biểu diễn số hữu tỉ: $\frac{3}{6} = \frac{1}{2} = 0,5$ $\frac{3}{6} = \frac{1}{2} = 0, 5$

+ Điểm D nằm cách O một đoạn bằng 8 đơn vị mới

=> Điểm D biểu diễn số hữu tỉ: $\frac{8}{6} = \frac{4}{3}$ $\frac{8}{6} = \frac{4}{3}$

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm B nằm cách O một đoạn bằng 2 đơn vị mới.

=> Điểm B biểu diễn số hữu tỉ: $- \frac{2}{6} = - \frac{1}{3}$ $- \frac{2}{6} = - \frac{1}{3}$

+ Điểm A nằm cách O một đoạn bằng 7 đơn vị mới

=> Điểm A biểu diễn số hữu tỉ: $- \frac{7}{6}$ $- \frac{7}{6}$

Bài 1.4 SGK Toán 7 tập 1 trang 9

a) Trong những phân số sau, những phân số nào biểu diễn số hữu tỉ -0,625?

$\frac{5}{{ - 8}};\frac{{10}}{{16}};\frac{{20}}{{ - 32}};\frac{{ - 10}}{{16}};\frac{{ - 25}}{{40}};\frac{{35}}{{ - 48}}$ $\frac{5}{- 8}; \frac{10}{16}; \frac{20}{- 32}; \frac{- 10}{16}; \frac{- 25}{40}; \frac{35}{- 48}$

b) Biểu diễn số hữu tỉ -0,625 trên trục số.

Hướng dẫn giải:

a) Ta có: $- 0,625 = - \frac{{625}}{{1000}} = - \frac{{625:125}}{{1000:125}} = - \frac{5}{8}$ $- 0, 625 = - \frac{625}{1000} = - \frac{625 : 125}{1000 : 125} = - \frac{5}{8}$

Ta lại có:

$- \frac{5}{8} = \frac{{ - 5.2}}{{8.2}} = \frac{{ - 10}}{{16}}$ $- \frac{5}{8} = \frac{- 5.2}{8.2} = \frac{- 10}{16}$

$- \frac{5}{8} = \frac{{ - 5.4}}{{8.4}} = \frac{{ - 20}}{{32}}$ $- \frac{5}{8} = \frac{- 5.4}{8.4} = \frac{- 20}{32}$

$- \frac{5}{8} = \frac{{ - 5.5}}{{8.5}} = \frac{{ - 25}}{{40}}$ $- \frac{5}{8} = \frac{- 5.5}{8.5} = \frac{- 25}{40}$

Suy ra $- 0,625 = - \frac{5}{8} = \frac{{ - 10}}{{16}} = \frac{{ - 20}}{{32}} = \frac{{ - 25}}{{40}}$ $- 0, 625 = - \frac{5}{8} = \frac{- 10}{16} = \frac{- 20}{32} = \frac{- 25}{40}$

Vậy những phân số biểu diễn số hữu tỉ -0,625 là $- \frac{5}{8};\frac{{ - 10}}{{16}};\frac{{ - 20}}{{32}};\frac{{ - 25}}{{40}}$ $- \frac{5}{8}; \frac{- 10}{16}; \frac{- 20}{32}; \frac{- 25}{40}$

b) Theo câu a ta có: $- 0,625 = - \frac{5}{8}$ $- 0, 625 = - \frac{5}{8}$ nên biểu diễn -0,625 trên trục số chính là biểu diễn phân số $- \frac{5}{8}$ $- \frac{5}{8}$ trên trục số.

Mô tả bằng hình vẽ như sau:

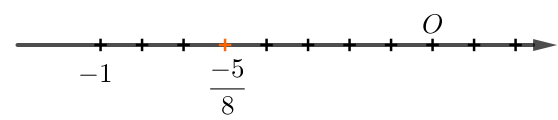
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ –0,625

Bước 1: Chia đoạn thẳng đơn vị thành 8 phần bằng nhau.

Bước 2: Lấy một điểm nằm về phía bên trái điểm O một đoạn bằng 5 đơn vị (đơn vị mới bằng $\frac{1}{8}$ $\frac{1}{8}$ đơn vị cũ)

Ta được điểm biểu diễn số hữu tỉ $- \frac{5}{8} = - 0,625$ $- \frac{5}{8} = - 0, 625$

Bài 1.5 SGK Toán 7 tập 1 trang 9

So sánh:

a) -2,5 và -2,125

b) $- \frac{1}{{10000}}$ $- \frac{1}{10000}$ và $\frac{1}{{23456}}$ $\frac{1}{23456}$

Hướng dẫn giải:

a) -2,5 và -2,125

Ta có: 2,5 < 2,125

=> -2,5 > -2,125

Vậy -2,5 > -2,125

b) $- \frac{1}{{10000}}$ $- \frac{1}{10000}$ và $\frac{1}{{23456}}$ $\frac{1}{23456}$

Ta có: $- \frac{1}{{10000}} < 0$ $- \frac{1}{10000} < 0$ và $\frac{1}{{23456}} > 0$ $\frac{1}{23456} > 0$

=> $- \frac{1}{{10000}} < 0 < \frac{1}{{23456}}$ $- \frac{1}{10000} < 0 < \frac{1}{23456}$

=> $- \frac{1}{{10000}} < \frac{1}{{23456}}$ $- \frac{1}{10000} < \frac{1}{23456}$

Vậy $- \frac{1}{{10000}} < \frac{1}{{23456}}$ $- \frac{1}{10000} < \frac{1}{23456}$

Bài 1.6 SGK Toán 7 tập 1 trang 9

Tuổi thị trung bình dự kiến của những người sinh năm 2019 ở một số quốc gia được cho trong bảng sau:

Quốc gia	Australia	Pháp	Tây Ban Nha	Anh	Mĩ
Tuổi thọ trung bình dự kiến	83	82,5	$83\frac{1}{5}$ $83 \frac{1}{5}$	$81\frac{2}{5}$ $81 \frac{2}{5}$	$78\frac{1}{2}$ $78 \frac{1}{2}$

(Theo Báo cáo của Tổ chức Y tế Thế giới, 2020)

Sắp xếp các quốc gia theo tuổi thọ trung bình dự kiến từ nhỏ tới lớn.

Hướng dẫn giải:

Để so sánh các số có thể so sánh các số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh các phân số đó.

Tây Ban Nha: $83\frac{1}{5} = 83 + \frac{1}{5} = 83 + 0,2 = 83,2$ $83 \frac{1}{5} = 83 + \frac{1}{5} = 83 + 0, 2 = 83, 2$

Anh: $81\frac{2}{5} = 81 + 0,4 = 81,4$ $81 \frac{2}{5} = 81 + 0, 4 = 81, 4$

Mĩ: $78\frac{1}{2} = 78 + \frac{1}{{22}} = 78 + 0,5 = 78,5$ $78 \frac{1}{2} = 78 + \frac{1}{22} = 78 + 0, 5 = 78, 5$

So sánh các số thập phân ta có:

78,5 < 81,4 < 82,5 < 83 < 83,2

=> $78\frac{1}{2} < 81\frac{2}{5} < 82,5 < 83 < 83\frac{1}{5}$ $78 \frac{1}{2} < 81 \frac{2}{5} < 82, 5 < 83 < 83 \frac{1}{5}$

Vậy sắp xếp các quốc gia theo tuổi thọ trung bình dự kiến từ nhỏ tới lớn như sau:

Mĩ --> Anh --> Pháp --> Australia --> Tây Ban Nha

C. Giải Toán 7 bài 1 sách Cánh Diều

Giải bài tập Toán 7 trang 10, 11 Tập hợp Q các số hữu tỉ tổng hợp lý thuyết, bài tập và đáp án cho các câu hỏi trong SGK Toán 7 tập 1 Cánh diều giúp các em học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 7 hiệu quả. Mời các bạn tham khảo chi tiết tại đây: Giải Toán 7 bài 1: Tập hợp Q các số hữu tỉ sách Cánh diều.

Bài 1 trang 10 SGK Toán 7 tập 1 Cánh diều

Các số $13, -29; -2,1; 2,28; \frac{{ - 12}}{{ - 18}}$ $13, - 29; - 2, 1; 2, 28; \frac{- 12}{- 18}$ có là số hữu tỉ không? Vì sao?

Hướng dẫn giải:

Các số $13, -29; -2,1; 2,28; \frac{{ - 12}}{{ - 18}}$ $13, - 29; - 2, 1; 2, 28; \frac{- 12}{- 18}$ có là số hữu tỉ vì:

$13 = \frac{{13}}{1}; - 29 = \frac{{ - 29}}{1}; - 2,1 = \frac{{21}}{{10}};2,28 = \frac{{228}}{{100}} = \frac{{54}}{{25}};\frac{{ - 12}}{{ - 18}} = \frac{2}{3}$ $13 = \frac{13}{1}; - 29 = \frac{- 29}{1}; - 2, 1 = \frac{21}{10}; 2, 28 = \frac{228}{100} = \frac{54}{25}; \frac{- 12}{- 18} = \frac{2}{3}$

Chú ý: Một số nguyên cũng là một số hữu tỉ.

Bài 2 trang 10 SGK Toán 7 tập 1 Cánh diều

Chọn kí hiệu “∈”; “∉” thích hợp cho dấu ?:

a) $21{\text{ }}?{\text{ }}\mathbb{Q}$ $21 ? Q$	b) $- 7{\text{ }}?{\text{ }}\mathbb{N}$ $- 7 ? N$
c) $\frac{5}{{ - 7}}{\text{ }}?{\text{ }}\mathbb{Z}$ $\frac{5}{- 7} ? Z$	d) $0{\text{ }}?{\text{ }}\mathbb{Q}$ $0 ? Q$
e) $- 7,3{\text{ }}?{\text{ }}\mathbb{Q}$ $- 7, 3 ? Q$	g) $3\frac{2}{9}{\text{ }}?{\text{ }}\mathbb{Q}$ $3 \frac{2}{9} ? Q$

Hướng dẫn giải:

a) Ta có: $21 = \frac{{21}}{1}$ $21 = \frac{21}{1}$

Do $21 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$ $21 \in Z, 1 \in Z, 1 \neq 0$ => 21 là số hữu tỉ

Vậy $21{\text{ }} \in {\text{ }}\mathbb{Q}$ $21 \in Q$

b) Ta có: -7 là số nguyên âm không thuộc tập số tự nhiên

Vậy $- 7{\text{ }} \notin {\text{ }}\mathbb{N}$ $- 7 \notin N$

c) Ta có: 5 : (-7) không phải là phép chia hết

=> $\frac{5}{{ - 7}}$ $\frac{5}{- 7}$ không thuộc tập số nguyên

Vậy $\frac{5}{{ - 7}}{\text{ }} \notin {\text{ }}\mathbb{Z}$ $\frac{5}{- 7} \notin Z$

d) Ta có: $0 = \frac{0}{1}$ $0 = \frac{0}{1}$

Do $0 \in \mathbb{Z},1 \in \mathbb{Z},1 \ne 0$ $0 \in Z, 1 \in Z, 1 \neq 0$ => 0 là số hữu tỉ

Vậy $0{\text{ }} \in {\text{ }}\mathbb{Q}$ $0 \in Q$

e) Ta có: $- 7,3 = \frac{{ - 73}}{{10}}$ $- 7, 3 = \frac{- 73}{10}$

Do $- 73 \in \mathbb{Z},10 \in \mathbb{Z},10 \ne 0$ $- 73 \in Z, 10 \in Z, 10 \neq 0$ => -7,3 là số hữu tỉ

Vậy $- 7,3{\text{ }} \in {\text{ }}\mathbb{Q}$ $- 7, 3 \in Q$

g) Ta có: $3\frac{2}{9} = \frac{{29}}{9}$ $3 \frac{2}{9} = \frac{29}{9}$

Do $29 \in \mathbb{Z},9 \in \mathbb{Z},9 \ne 0$ $29 \in Z, 9 \in Z, 9 \neq 0$ => $3\frac{2}{9}$ $3 \frac{2}{9}$ là số hữu tỉ

Vậy $3\frac{2}{9}{\text{ }} \in {\text{ }}\mathbb{Q}$ $3 \frac{2}{9} \in Q$

Bài 3 trang 10 SGK Toán 7 tập 1 Cánh diều

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) Nếu $a \in \mathbb{N}$ $a \in N$ thì $a \in \mathbb{Q}$ $a \in Q$	b) Nếu $a \in \mathbb{Z}$ $a \in Z$ thì $a \in \mathbb{Q}$ $a \in Q$
c) Nếu $a \in \mathbb{Q}$ $a \in Q$ thì $a \in \mathbb{Q}$ $a \in Q$	d) Nếu $a \in \mathbb{Q}$ $a \in Q$ thì $a \in \mathbb{Z}$ $a \in Z$
e) Nếu $a \in \mathbb{N}$ $a \in N$ thì $a \in \mathbb{Q}$ $a \in Q$	g) Nếu $a \in \mathbb{Z}$ $a \in Z$ thì $a \notin \mathbb{Q}$ $a \notin Q$

Hướng dẫn giải:

a) Mọi số tự nhiên m bất kỳ đều biểu diễn được dưới dạng phân số $\frac{m}{1}$ $\frac{m}{1}$

=> Nếu m là số tự nhiên thì m cũng là số hữu tỉ.

=> Phát biểu a đúng.

b) Mọi số nguyên m bất kỳ đều biểu diễn được dưới dạng phân số $\frac{m}{1}$ $\frac{m}{1}$

=> Nếu m là số nguyên thì m cũng là số hữu tỉ.

=> Phát biểu b đúng

c) Nếu m là số hữu tỉ thì m có thể là số tự nhiên.

Ví dụ: -3 vừa là số hữu tỉ vừa là số tự nhiên.

Nếu m là số hữu tỉ thì m có thể không phải là số tự nhiên.

Ví dụ: $\frac{5}{6}$ $\frac{5}{6}$ là số hữu tỉ nhưng không phải là số tự nhiên.

=> Nếu m là số hữu tỉ thì m chưa chắc là số tự nhiên.

=> Phát biểu c sai.

d) Nếu m là số hữu tỉ thì m có thể là số nguyên.

Ví dụ: −2 vừa là số hữu tỉ vừa là số nguyên.

Nếu m là số hữu tỉ thì m có thể không phải là số nguyên.

Ví dụ: $\frac{1}{3}$ $\frac{1}{3}$ là số hữu tỉ nhưng không phải là số nguyên.

=> Nếu m là số hữu tỉ thì m chưa chắc là số nguyên.

=> Phát biểu d sai

e) Mọi số tự nhiên m bất kỳ đều biểu diễn được dưới dạng phân số $\frac{m}{1}$ $\frac{m}{1}$

=> Nếu m là số tự nhiên thì m cũng là số hữu tỉ.

=> Phát biểu e sai.

g) Mọi số nguyên m bất kỳ đều biểu diễn được dưới dạng phân số $\frac{m}{1}$ $\frac{m}{1}$

=> Nếu m là số nguyên thì m cũng là số hữu tỉ.

=> Phát biểu g sai.

Bài 4 trang 11 SGK Toán 7 tập 1 Cánh diều

Quan sát trục số sau và cho biết điểm A, B, C, D biểu diễn những số nào:

Bài 4 trang 11 Toán 7 tập 1 SGK Cánh Diều

Hướng dẫn giải:

- Đoạn thẳng đơn vị chia thành 7 đoạn thẳng bằng nhau, đơn vị mới bằng $\frac{1}{7}$ $\frac{1}{7}$ đơn vị cũ.

Quan sát phần hình vẽ phía bên phải điểm O:

+ Điểm C nằm cách O một đoạn bằng 2 đơn vị mới.

=> Điểm C biểu diễn số hữu tỉ: $\frac{2}{7}$ $\frac{2}{7}$

+ Điểm D nằm cách O một đoạn bằng 6 đơn vị mới

=> Điểm D biểu diễn số hữu tỉ: $\frac{6}{7}$ $\frac{6}{7}$

Quan sát phần hình vẽ phía bên trái điểm O (các số hữu tỉ là các số âm)

+ Điểm B nằm cách O một đoạn bằng 3 đơn vị mới.

=> Điểm B biểu diễn số hữu tỉ: $- \frac{3}{7}$ $- \frac{3}{7}$

+ Điểm A nằm cách O một đoạn bằng 9 đơn vị mới

=> Điểm A biểu diễn số hữu tỉ: $- \frac{9}{7}$ $- \frac{9}{7}$

D. Giải Toán lớp 7 bài 1 sách cũ

I. Tóm tắt lý thuyết tập hợp Q các số hữu tỉ

1. Số hữu tỉ: Số hữu tỉ là số có thể viết dưới dạng a/b với a, b ∈ Z, b ≠ 0 và được kí hiệu là Q

2. Biểu diễn số hữu tỉ trên trục số:

Mỗi số hữu tỉ được biểu diễn bởi một điểm trên trục số và không phụ thuộc vào cách chọn phân số xác định nó

3. So sánh số hữu tỉ. Để so sánh hai số hữu tỉ x, y ta làm như sau:

Viết x, y dưới dạng phân số cùng mẫu dương

x = $\frac{a}{m}$ $\frac{a}{m}$ ; y = $\frac{b}{m}$ $\frac{b}{m}$ (m > 0)

So sánh các tử là số nguyên a và b

Nếu a > b thì x > y
Nếu a = b thì x=y
Nếu a < b thì x < y

4. Chú ý:

Số hữu tỉ lớn hơn 0 gọi là số hữu tỉ dương
Số hữu tỉ nhỏ hơn 0 gọi là số hữu tỉ âm
Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm

II. Giải bài tập Toán 7 tập 1 trang 5, 6, 7 câu 1, 2, 3, 4, 5

1. Trả lời câu hỏi 1 Bài 1 trang 5 SGK Toán 7 Tập 1

Vì sao các số 0,6 ; -1,25; $1\frac{1}{3}$ $1 \frac{1}{3}$ là các số hữu tỉ ?

Hướng dẫn giải:

Các số 0,6; −1,25; −1,25; $1\frac{1}{3}$ $1 \frac{1}{3}$ là các số hữu tỉ vì:

0,6 = $\frac{6}{10}$ $\frac{6}{10}$

−1,25 = $\frac{-125}{100}$ $\frac{- 125}{100}$

$1\frac{1}{3}$ $1 \frac{1}{3}$ = 1 + $\frac{1}{3}$ $\frac{1}{3}$ = $\frac{4}{3}$ $\frac{4}{3}$

Hay các số 0,6; −1,25; $1\frac{1}{3}$ $1 \frac{1}{3}$ viết được dưới dạng phân số $\frac{a}{b}$ $\frac{a}{b}$ với a, b ∈Z và b ≠ 0 nên các số đó là các số hữu tỉ.

2. Trả lời câu hỏi 2 Bài 1 trang 5 SGK Toán 7 Tập 1.

Số nguyên a có là số hữu tỉ không? Vì sao?

Hướng dẫn giải:

Số nguyên a luôn viết được dưới dạng $\frac{c}{d}$ $\frac{c}{d}$ (c, d ∈ Z; d ≠ 0) do đó a là số hữu tỉ.

Ví dụ:

3 = $\frac{3}{1}$ $\frac{3}{1}$ = $\frac{−3}{−1}$ $\frac{- 3}{- 1}$ = $\frac{6}{2}$ $\frac{6}{2}$

−2 = $\frac{−2}{1}$ $\frac{- 2}{1}$

3. Trả lời câu hỏi 3 Bài 1 trang 5 SGK Toán 7 Tập 1.

Biểu diễn các số nguyên: -1; 1; 2 trên trục số.

Hướng dẫn giải:

- Số nguyên -1 được biểu diễn bởi điểm A nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 1 đơn vị

- Số nguyên 1 được biểu diễn bởi điểm B nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 1 đơn vị

- Số nguyên 2 được biểu diễn bởi điểm C nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị

Ta biểu diễn trên trục số như sau:

Giải bài tập Toán 7

4. Trả lời câu hỏi 4 Bài 1 trang 6 SGK Toán 7 Tập 1.

So sánh hai phân số: $\frac{−2}{3}$ $\frac{- 2}{3}$ và $\frac{4}{−5}$ $\frac{4}{- 5}$

Hướng dẫn giải:

Ta có:

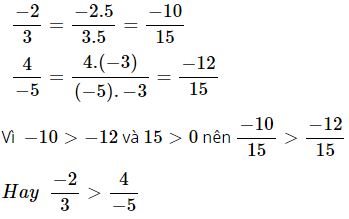
Giải bài tập Toán 7

5. Trả lời câu hỏi 5 Bài 1 trang 7 SGK Toán 7 Tập 1.

Trong các số hữu tỉ sau, số nào là số hữu tỉ dương, số nào là số hữu tỉ âm, số nào không là số hữu tỉ dương cũng không là số hữu tỉ âm ?

$\frac{−3}{7}$ $\frac{- 3}{7}$ ; $\frac{2}{3}$ $\frac{2}{3}$ ; $\frac{1}{−5}$ $\frac{1}{- 5}$ ; −4; $\frac{0}{−2}$ $\frac{0}{- 2}$ ; $\frac{-3}{-5}$ $\frac{- 3}{- 5}$

Hướng dẫn giải:

Số hữu tỉ dương là: $\frac{2}{3}$ $\frac{2}{3}$ , $\frac{-3}{-5}$ $\frac{- 3}{- 5}$

Số hữu tỉ âm là: $\frac{−3}{7}$ $\frac{- 3}{7}$ ; $\frac{1}{−5}$ $\frac{1}{- 5}$ ; −4

Số hữu tỉ không là số hữu tỉ dương cũng không là số hữu tỉ âm là: $\frac{0}{−2}$ $\frac{0}{- 2}$

F. Giải Toán 7 tập 1 trang 7, 8 bài 1, 2, 3, 4, 5

1. Giải bài tập Toán 7 Bài 1 (trang 7 SGK Toán đại số lớp 7 tập 1)

Điền kí hiệu (∈, ⊂, ∉) thích hợp vào ô vuông

– 3 ... N ; -3 ... Z; -3...Q

-2/3 ... Z; -2/3... Q; N... Z... Q

Đáp án và hướng dẫn giải bài 1:

– 3 ∉ N – 3 ∈ Z -3 ∈ Q

-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q

2. Giải bài tập Toán 7 Bài 2 (trang 7 SGK Toán đại số lớp 7 tập 1)

Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{3}{-4}$ $\frac{3}{- 4}$

Đáp án và hướng dẫn giải bài 2:

Bài tập môn Toán lớp 7

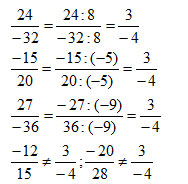
Vậy những phân số biểu diễn số hữu tỉ $\frac{3}{-4}$ $\frac{3}{- 4}$ là: $\frac{-15}{20}$ $\frac{- 15}{20}$ ; $\frac{24}{-32}$ $\frac{24}{- 32}$ ; $\frac{-27}{36}$ $\frac{- 27}{36}$

3. Giải bài tập Toán 7 Bài 3 (trang 8 SGK Toán đại số lớp 7 tập 1)

So sánh các số hữu tỉ:

a) x = 2/ -7 và y = -3/11

b) x = -213/300 và y = 18/-25

c) x = -0,75 và y = - 3/4

Đáp án và hướng dẫn giải bài 3:

a) x= 2/-7 = -22/7;y = -3/11= -21/77

Vì -22 < -21 và 77> 0 nên x <y

Bài tập môn Toán lớp 7

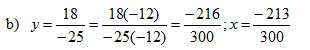
Vì -216 < -213 và 300 > 0 nên y < x

c) x = -0,75 = -75/100 = -3/4; y = -3/4

Vậy x = y

4. Giải bài tập Toán 7 Bài 4 (trang 8 SGK Toán đại số lớp 7 tập 1)

So sánh số hữu tỉ a/b (a,b ∈ Z, b ≠ 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu

Đáp án và hướng dẫn giải bài 4:

Với a, b ∈ Z, b> 0

Khi a, b cùng dấu thì a/b > 0

Khi a,b khác dấu thì a/b < 0

Tổng quát: Số hữu tỉ a/b (a, b ∈ Z, b ≠ 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

5. Giải bài tập Toán 7 Bài 5 (trang 8 SGK Toán đại số lớp 7 tập 1)

Giả sử x = a/m; y = b/m

(a, b, m ∈ Z, b ≠ 0) và x < y. Hãy chứng tỏ rằng nếu chọn z = (a+b)/2m thì ta có x < z < y

Đáp án và hướng dẫn giải bài 5:

Theo đề bài ta có x = a/ m; y = b/m (a, b, m ∈ Z, m > 0)

Vì x < y nên ta suy ra a< b

Ta có:

Bài tập môn Toán lớp 7

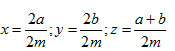
Vì a < b ⇒ a + a < a +b ⇒ 2a < a + b

Do 2a < a +b nên x < z (1)

Vì a < b ⇒ a + b < b + b ⇒ a + b < 2b

Do a+b < 2b nên z < y (2)

Từ (1) và (2) ta suy ra x < z< y

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

220

83.688

Bài trước

Bài sau

Chia sẻ bởi:
Nguyễn Thị Phương

Tải về

Chọn file muốn tải về:

Giải Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!