VnDoc.com

30 đề thi học sinh giỏi Toán lớp 7 CÓ ĐÁP ÁN

Đề thi học sinh giỏi lớp 7 môn Toán có đáp án

Bài trước

Tải về

Bài sau

Lớp: Lớp 7

Môn: Toán

Dạng tài liệu: Đề thi HSG

Loại File: Word + PDF

Phân loại: Tài liệu Cao cấp

Đây là tài liệu Cao cấp - Chỉ dành cho Thành viên VnDoc ProPlus.

Tải tất cả tài liệu lớp 7 (Trừ Giáo án, bài giảng)
Trắc nghiệm không giới hạn

Mua ProPlus 369.000đ

Tài liệu 30 đề thi học sinh giỏi Toán lớp 7 có đáp án giúp các em rèn luyện kỹ năng giải toán, chuẩn bị tốt cho kỳ thi học sinh giỏi. Các đề đa dạng, từ cơ bản đến nâng cao, kèm đáp án chi tiết, sẽ là người bạn đồng hành, giúp các em chinh phục môn Toán! Đối với các thầy cô, tài liệu này sẽ hỗ trợ xây dựng bài giảng, ôn tập và bồi dưỡng học sinh, với đáp án chi tiết giúp tiết kiệm thời gian soạn bài.

Để tải trọn vẹn 30 đề thi học sinh giỏi Toán lớp 7 CÓ ĐÁP ÁN, mời các bạn kích vào nút Tải về phía cuối bài.

Mời các bạn tham khảo thêm: 225 đề thi học sinh giỏi môn Toán lớp 7 CÓ ĐÁP ÁN

Tuyển tập 30 đề thi HSG Toán 7 có đáp án

Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 1
Đáp án Đề thi học sinh giỏi lớp 7 môn Toán số 1
Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 2
Đáp án Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 2

Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 1

Bài 1: (3 điểm): Tính

$\left[ {18\frac{1}{6} - \left( {0,06:7\frac{1}{2} + 3\frac{2}{5}.0,38} \right)} \right]:\left( {19 - 2\frac{2}{3}.4\frac{3}{4}} \right)$ $\left[ {18\frac{1}{6} - \left( {0,06:7\frac{1}{2} + 3\frac{2}{5}.0,38} \right)} \right]:\left( {19 - 2\frac{2}{3}.4\frac{3}{4}} \right)$

Bài 2: (4 điểm) Cho $\frac{a}{c} = \frac{c}{b}$ $\frac{a}{c} = \frac{c}{b}$ chứng minh rằng:

a. $\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}$ $\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}$

b. $\frac{{{b^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}$ $\frac{{{b^2} - {a^2}}}{{{a^2} + {c^2}}} = \frac{{b - a}}{a}$

Bài 3: (4 điểm): Tìm x biết:

a. $\left| {x + \frac{1}{5}} \right| - 4 = - 2$ $\left| {x + \frac{1}{5}} \right| - 4 = - 2$

b. $- \frac{{15}}{{12}}x + \frac{3}{7} = \frac{6}{5}x - \frac{1}{2}$ $- \frac{{15}}{{12}}x + \frac{3}{7} = \frac{6}{5}x - \frac{1}{2}$

Bài 4: (3 điểm) Một vật chuyển động trên các cạnh hình vuông. Trên hai cạnh đầu vật chuyển động với vận tốc 5m/s, trên cạnh thứ ba với vận tốc 4m/s, trên cạnh thứ tư với vận tốc 3m/s. Hỏi độ dài cạnh hình vuông biết rằng tổng thời gian vật chuyển động trên bốn cạnh là 59 giây.

Bài 5: (4 điểm) Cho tam giác ABC cân tại A có A = 20⁰, vẽ tam giác đều DBC (D nằm trong tam giác ABC). Tia phân giá của góc ABD cắt AC tại M. Chứng minh:

a) Tia AD là phân giác của góc BAC

b) AM = BC

Bài 6: (2 điểm): Tìm x , y ∈ N biết: 25 - y ² = 8( x - 2009)²

Đáp án Đề thi học sinh giỏi lớp 7 môn Toán số 1

Bài 1.

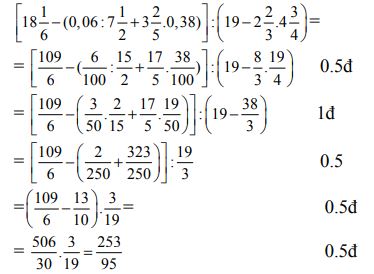
30 đề thi HSG Toán 7 có đáp án

Bài 2

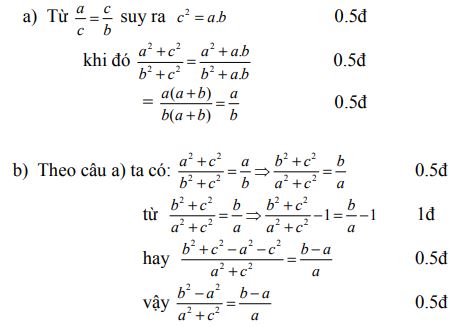
30 đề thi HSG Toán 7 có đáp án

Bài 3

30 đề thi HSG Toán 7 có đáp án

Bài 4

Cùng một đoạn đường, vận tốc và thời gian là hai đại lượng tỉ lệ nghịch.

Gọi x, y, z là thời gian chuyển động lần lượt với các vận tốc 5m/s; 4m/s; 3m/s.

Ta có: 5x = 4y = 3z và x + y + z = 59

Hay $\dfrac{x}{{\dfrac{1}{5}}} = \dfrac{y}{{\dfrac{1}{4}}} = \frac{z}{{\dfrac{1}{3}}} = \dfrac{{x + y + z}}{{\dfrac{1}{5} + \dfrac{1}{4} + \dfrac{1}{3}}} = \dfrac{{59}}{{\dfrac{{59}}{{60}}}} = 60$ $\dfrac{x}{{\dfrac{1}{5}}} = \dfrac{y}{{\dfrac{1}{4}}} = \frac{z}{{\dfrac{1}{3}}} = \dfrac{{x + y + z}}{{\dfrac{1}{5} + \dfrac{1}{4} + \dfrac{1}{3}}} = \dfrac{{59}}{{\dfrac{{59}}{{60}}}} = 60$

Do đó: x = 60. $\frac{1}{5}$ $\frac{1}{5}$ = 12

y = 60. $\frac{1}{4}$ $\frac{1}{4}$ = 15

z = 60. $\frac{1}{3}$ $\frac{1}{3}$ = 20

Vậy cạnh hình vuông là 5.12 = 60m

Bài 5

Vẽ hình, ghi GT, KL đúng 0,5đ

a. Chứng minh ΔADB = ΔADC (c - c - c) 1đ

Suy ra $\widehat {DAB} = \widehat {DAC}$ $\widehat {DAB} = \widehat {DAC}$

Do đó: $\widehat {DAB}$ $\widehat {DAB}$ = 20⁰ : 2 = 10⁰

b. Ta có: ΔABC cân tại A, mà $\widehat A$ $\widehat A$ = 20⁰ (gt) nên $\widehat {ABC}$ $\widehat {ABC}$ = (180⁰ - 20⁰) : 2 = 80⁰

ΔABC đều nên $\widehat {DBC}$ $\widehat {DBC}$ = 60⁰

Tia BD nằm giữa hai tia BA và BC suy ra $\widehat {ABD}$ $\widehat {ABD}$ = 80⁰ - 60⁰ = 20⁰

Tia BM là tia phân giác của góc ABD nên $\widehat {ABM}$ $\widehat {ABM}$ = 10⁰

Xét ΔABM và ΔBAD ta có:

AB là cạnh chung

$\begin{gathered} \widehat {BAM} = \widehat {ABD} = {20^0} \hfill \\ \widehat {ABM} = \widehat {DAB} = {10^0} \hfill \\ \end{gathered}$ $\begin{gathered} \widehat {BAM} = \widehat {ABD} = {20^0} \hfill \\ \widehat {ABM} = \widehat {DAB} = {10^0} \hfill \\ \end{gathered}$

Vậy ΔABM = ΔBAD (g - c - g)

Suy ra AM = BD, mà BD = BC (gt) nên AM = BC

Bài 6

25 - y² = 8(x - 2009)²

Ta có: 8(x - 2009)² = 25 - y²

8(x - 2009)² + y2 = 25 (*)

Vì y² ≥ 0 nên (x - 2009)² ≤ $\dfrac{25}{8}$ $\dfrac{25}{8}$⇒ (x- 2009)² = 0 hoặc (x - 2009)² = 1

Với (x - 2009)² = 0 thay vào (*) ta được y² = 17 (loại)

Với (x - 2009)² = 1 thay vào (*) ta có y² = 25 suy ra y = 5 (do y ∈ $\mathbb{N}$ $\mathbb{N}$)

Từ đó tìm được x = 2009; y = 5

Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 2

Câu 1: Với mọi số tự nhiên n ≥ 2 hãy so sánh:

a. $A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}$ $A = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + ... + \frac{1}{{{n^2}}}$ với 1

b. $B = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{\left( {2n} \right)}^2}}}$ $B = \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{6^2}}} + ... + \frac{1}{{{{\left( {2n} \right)}^2}}}$ với 0,5

Câu 2: Tìm phần nguyên của α, với α = $\sqrt 2 + \sqrt[3]{{\frac{3}{2}}} + \sqrt[3]{{\frac{4}{3}}} + ... + \sqrt[{n + 1}]{{\frac{{n + 1}}{n}}}$ $\sqrt 2 + \sqrt[3]{{\frac{3}{2}}} + \sqrt[3]{{\frac{4}{3}}} + ... + \sqrt[{n + 1}]{{\frac{{n + 1}}{n}}}$

Câu 3: Tìm tỉ lệ 3 cạnh của một tam giác, biết rằng cộng lần lượt độ dài hai đường cao của tam giác đó thì tỉ lệ các kết quả là 5: 7: 8.

Câu 4: Cho góc xOy, trên hai cạnh Ox và Oy lần lượt lấy các điểm A và B để cho AB có độ dài nhỏ nhất.

Câu 5: Chứng minh rằng nếu a, b, c và $\sqrt a + \sqrt b + \sqrt c$ $\sqrt a + \sqrt b + \sqrt c$ là các số hữu tỉ.

Đáp án Đề thi học sinh giỏi lớp 7 môn Toán - Đề số 2

Câu 1: (2 điểm)

Do $\frac{1}{{{n^2}}} < \frac{1}{{{n^2} - 1}}$ $\frac{1}{{{n^2}}} < \frac{1}{{{n^2} - 1}}$ với mọi n ≥ 2 nên

A < C = $\frac{1}{{{2^2} - 1}} + \frac{1}{{{3^2} - 1}} + ... + \frac{1}{{{n^2} - 1}}$ $\frac{1}{{{2^2} - 1}} + \frac{1}{{{3^2} - 1}} + ... + \frac{1}{{{n^2} - 1}}$

Mặt khác:

$\begin{matrix} C = \dfrac{1}{{1.3}} + \dfrac{1}{{2.4}} + \dfrac{1}{{3.5}} + ... + \dfrac{1}{{\left( {n - 1} \right)\left( {n + 1} \right)}} \hfill \\ C = \dfrac{1}{2}\left( {\dfrac{1}{1} - \dfrac{1}{3} + \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{3} - \dfrac{1}{5} + ... + \dfrac{1}{{n - 1}} - \dfrac{1}{{n + 1}}} \right) \hfill \\ C = - \left( {1 + \dfrac{1}{2} - \dfrac{1}{n} - \dfrac{1}{{n + 1}}} \right) < \dfrac{1}{2}.\dfrac{3}{2} = \dfrac{3}{4} < 1 \hfill \\ \end{matrix}$ $\begin{matrix} C = \dfrac{1}{{1.3}} + \dfrac{1}{{2.4}} + \dfrac{1}{{3.5}} + ... + \dfrac{1}{{\left( {n - 1} \right)\left( {n + 1} \right)}} \hfill \\ C = \dfrac{1}{2}\left( {\dfrac{1}{1} - \dfrac{1}{3} + \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{3} - \dfrac{1}{5} + ... + \dfrac{1}{{n - 1}} - \dfrac{1}{{n + 1}}} \right) \hfill \\ C = - \left( {1 + \dfrac{1}{2} - \dfrac{1}{n} - \dfrac{1}{{n + 1}}} \right) < \dfrac{1}{2}.\dfrac{3}{2} = \dfrac{3}{4} < 1 \hfill \\ \end{matrix}$

Vậy A < 1

b. (1 điểm)

$\begin{matrix} B = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{\left( {2n} \right)}^2}}} \hfill \\ B = \dfrac{1}{{{2^2}}}\left( {1 + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + .... + \dfrac{1}{{{n^2}}}} \right) \hfill \\ B = \dfrac{1}{{{2^2}}}\left( {1 + A} \right) \hfill \\ \end{matrix}$ $\begin{matrix} B = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{4^2}}} + ... + \dfrac{1}{{{{\left( {2n} \right)}^2}}} \hfill \\ B = \dfrac{1}{{{2^2}}}\left( {1 + \dfrac{1}{{{2^2}}} + \dfrac{1}{{{3^2}}} + .... + \dfrac{1}{{{n^2}}}} \right) \hfill \\ B = \dfrac{1}{{{2^2}}}\left( {1 + A} \right) \hfill \\ \end{matrix}$

Suy ra P < 0,5

Câu 2 (2 điểm):

Ta có: $\sqrt[{k + 1}]{{\frac{{k + 1}}{k}}} > 1,\left( {k = \overline {1,n} } \right)$ $\sqrt[{k + 1}]{{\frac{{k + 1}}{k}}} > 1,\left( {k = \overline {1,n} } \right)$

Áp dụng bất đẳng thức Cauchy cho k + 1 số ta có:

$\begin{matrix} \sqrt[{k + 1}]{{\dfrac{{k + 1}}{k}}} = \sqrt[{k + 1}]{{\dfrac{{1 + 1 + .... + 1}}{k}\dfrac{{k + 1}}{k}}} < \dfrac{{1 + 1 + ... + 1 + \dfrac{{k + 1}}{k}}}{{k + 1}} = \dfrac{k}{{k + 1}} + \dfrac{1}{k} = 1 + \dfrac{1}{{k\left( {k + 1} \right)}} \hfill \\ \Rightarrow 1 < \sqrt[{k + 1}]{{\dfrac{{k + 1}}{k}}} < 1 + \left( {\dfrac{1}{k} - \dfrac{1}{{k + 1}}} \right) \hfill \\ \end{matrix}$ $\begin{matrix} \sqrt[{k + 1}]{{\dfrac{{k + 1}}{k}}} = \sqrt[{k + 1}]{{\dfrac{{1 + 1 + .... + 1}}{k}\dfrac{{k + 1}}{k}}} < \dfrac{{1 + 1 + ... + 1 + \dfrac{{k + 1}}{k}}}{{k + 1}} = \dfrac{k}{{k + 1}} + \dfrac{1}{k} = 1 + \dfrac{1}{{k\left( {k + 1} \right)}} \hfill \\ \Rightarrow 1 < \sqrt[{k + 1}]{{\dfrac{{k + 1}}{k}}} < 1 + \left( {\dfrac{1}{k} - \dfrac{1}{{k + 1}}} \right) \hfill \\ \end{matrix}$

Lần lượt cho k = 1, 2, 3, ... rồi cộng lại ta được

$n < \sqrt 2 + \sqrt[3]{{\frac{3}{2}}} + ... + \sqrt[{n + 1}]{{\frac{{n + 1}}{n}}} < n + 1 - \frac{1}{n} < n + 1 \Rightarrow \left| \alpha \right| = n$ $n < \sqrt 2 + \sqrt[3]{{\frac{3}{2}}} + ... + \sqrt[{n + 1}]{{\frac{{n + 1}}{n}}} < n + 1 - \frac{1}{n} < n + 1 \Rightarrow \left| \alpha \right| = n$

Đừng quên chia sẻ với bạn bè bộ đề thi học sinh giỏi môn Toán lớp 7 kèm đáp án chi tiết trên để cùng nhau tiến bộ nhé! Chúc các em học tốt và đạt thành tích cao!

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 7. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Để ôn luyện chuẩn bị cho kì thi học sinh giỏi lớp 7 sắp tới, mời các bạn vào chuyên mục Thi học sinh giỏi lớp 7 trên VnDoc nhé. Chuyên mục tổng hợp các đề thi học sinh giỏi của tất cả các môn, là tài liệu hay cho các em ôn tập và luyện đề.

	Đặt câu hỏi về học tập, giáo dục, giải bài tập của bạn tại chuyên mục Hỏi đáp của VnDoc
Hỏi - Đáp	Truy cập ngay: Hỏi - Đáp học tập