Giải bài tập SGK Toán lớp 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)

Giải bài tập Toán lớp 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g)

Giải bài tập SGK Toán lớp 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác góc - cạnh - góc (g.c.g) với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 7. Lời giải hay bài tập Toán 7 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo

Trả lời câu hỏi Toán 7 Tập 1 Bài 5 trang 121: Vẽ thêm tam giác A’B’C’ có: B’C’ = 4cm; ∠B' = 60^o; ∠C' = 40^o. Hãy đo để kiểm nghiệm rằng AB = A’B’. Vì sao ta kết luận được ΔABC = ΔA’B’C’?

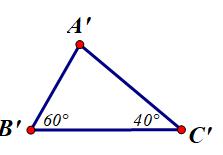
Lời giải

ΔABC và ΔA’B’C’ có:

AB = A’B’

∠B = ∠B'

BC = B’C’

⇒ ΔABC = ΔA’B’C’ (cạnh – góc – cạnh)

Trả lời câu hỏi Toán 7 Tập 1 Bài 5 trang 122: Tìm các tam giác bằng nhau ở mỗi hình 94, 95, 96

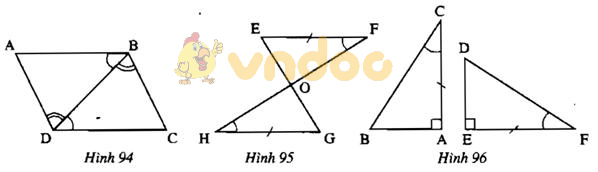
Lời giải

- Hình 94:

ΔABD và ΔCDB có

∠(ABD) = ∠(BDC) (gt)

BD cạnh chung

∠(ADB) = ∠(DBC)

Nên ΔABD = ΔCDB (g.c.g)

- Hình 95

Ta có: ∠(EFO) + ∠(FEO) + ∠(EOF) = ∠(GHO) + ∠(HGO) + ∠(GOH) = 180^o

∠(EFO) = ∠(GHO) (Gt)

∠(EOF) = ∠(GOH) (hai góc đối đỉnh)

⇒ ∠(FEO) + ∠(HGO)

ΔEOF và ΔGOH có

∠(EFO) = ∠(OHG) (gt)

EF = GH (gt)

∠(FEO) = ∠(HGO) (CMT)

Nên ΔEOF = ΔGOH (g.c.g)

- Hình 96

ΔABC và ΔEDF có

∠(BAC)= ∠(DEF) (gt)

AC = EF

∠(ACB) = ∠(EFD)

Nên ΔABC = ΔEDF (g.c.g)

Bài 33 (trang 123 SGK Toán 7 Tập 1): Vẽ tam giác ABC biết

Lời giải:

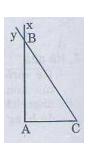
Cách vẽ:

- Vẽ đoạn thẳng AC = 2cm

- Trên cùng một nửa mặt phẳng bờ AC vẽ các tia Ax và Cy sao cho

Hai tia cắt nhau tại B. Ta được tam giác ABC cần vẽ.

Bài 34 (trang 123 SGK Toán 7 Tập 1): Trên mỗi hình 98, 99 có các tam giác nào bằng nhau? Vì sao?

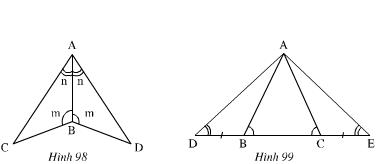
Lời giải:

- Hình 98): Xét ΔABC và ΔABD có:

Nên ΔABC = ΔABD (g.c.g)

- Hình 99): Ta có:

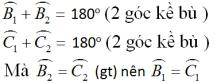
Xét ΔABD và ΔACE có:

Nên ΔABD = ΔACE ( g.c.g)

Xét ΔADC và ΔAEB có:

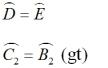
DC = EB (Vì DC = DB + BC; EB = EC + BC mà DB = EC)

Nên ΔADC = ΔAEB (g.c.g)

Bài 35 (trang 123 SGK Toán 7 Tập 1): Cho góc xOy khác gọc bẹt Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với tia Ot, nó cắt Ox và Oy theo thứ tự ở A và B.

a) Chứng minh rằng OA = OB

b) Lấy điểm C thuộc tia Ot. Chứng minh rằng

Lời giải:

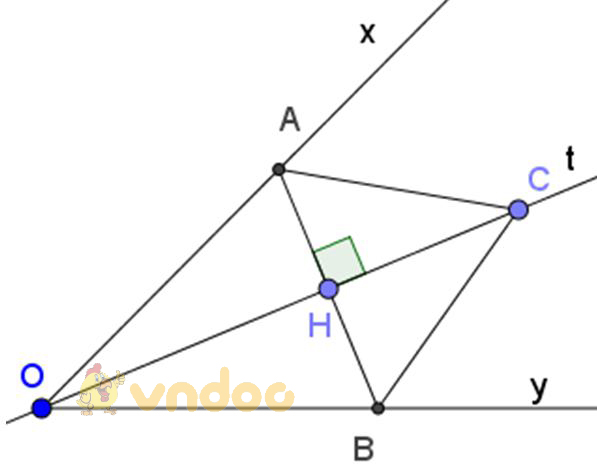
a) Xét ΔAOH và ΔBOH có:

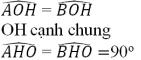
Nên ΔAOH = ΔBOH (g.c.g)

Vậy OA = OB

b) Xét ΔAOC = ΔBOC có:

OA = OB (cmt)

OC cạnh chung

Nên ΔAOC = ΔBOC (g.c.g)

Suy ra CA = CB (cạnh chung)

Bài 36 (trang 123 SGK Toán 7 Tập 1): Trên hình 100 ta có OA = OB, góc OAC = góc OBD. Chứng minh rằng AC = BD

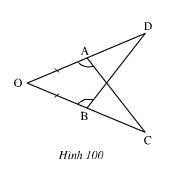
Lời giải:

Xét ΔOAC và ΔOBD có:

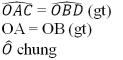
Nên ΔOAC = ΔOBD (g.c.g)

Suy ra AC = BD

Bài 37 (trang 123 SGK Toán 7 Tập 1): Trên mỗi hình 101, 102, 103 có các tam giác nào bằng nhau? Vì sao?

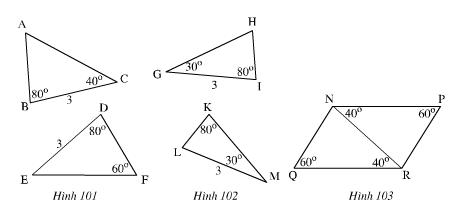
Lời giải:

Tính các góc còn lại trên mỗi hình ta được:

Ta có ΔABC = ΔFDE (g.c.g) vì:

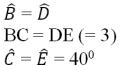
ΔNQR = ΔRPN (g.c.g) vì

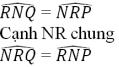
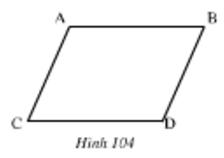
Bài 38 (trang 124 SGK Toán 7 Tập 1): Trên hình 104 ta có AB // CD, AC // BD. Hãy chứng minh rằng AB = CD, AC = BD.

Lời giải:

Kí hiệu góc như hình dưới:

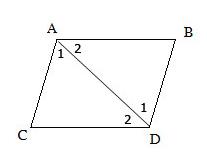
Vẽ đoạn thẳng AD

Xét ΔABD và ΔDAC có:

Do đó ΔABD = ΔDAC (g.c.g)

Suy ra AB = CD; BD = AC (đpcm)

Bài 39 (trang 124 SGK Toán 7 Tập 1): Trên mỗi hình 105, 106, 107, 108 có các tam giác vuông nào bằng nhau? Vì sao?

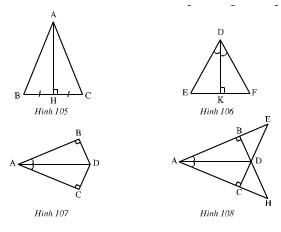
Lời giải:

- Hình 105

Xét ΔABH và ΔACH có:

BH = CH (gt)

Vậy ΔABH = ΔACH (c.g.c)

- Hình 106

Xét Δ DKE và ΔDKF có:

Vậy ΔDKE = ΔDKF (g.c.g)

- Hình 107

Ta có ΔABD = ΔACD (cạnh huyền – góc nhọn)

- Hình 108

Làm tương tự ta có ΔABD = ΔACD

ΔDBE = ΔDCH

ΔABH = ΔACE

Bài 40 (trang 124 SGK Toán 7 Tập 1): Cho ΔABC tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E, F thuộc Ax). So sánh các độ dài BE và CF.