Giải bài tập SGK Toán lớp 7 bài 7: Tính chất đường trung trực của một đoạn thẳng
Giải bài tập Toán lớp 7 bài 7: Tính chất đường trung trực của một đoạn thẳng
Giải bài tập SGK Toán lớp 7 bài 7: Tính chất đường trung trực của một đoạn thẳng với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 7. Lời giải hay bài tập Toán 7 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo
Giải bài tập SGK Toán lớp 7 bài 4: Tính chất ba đường trung tuyến của tam giác
Giải bài tập SGK Toán lớp 7 bài 5: Tính chất tia phân giác của một góc
Giải bài tập SGK Toán lớp 7 bài 6: Tính chất ba đường phân giác của tam giác
Trả lời câu hỏi Toán 7 Tập 2 Bài 7 trang 75: Hãy viết giả thiết, kết luận của định lí.
Lời giải
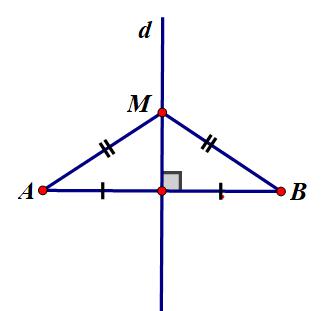
- Giả thiết: ΔABM có d là đường trung trực
MA = MB
- Kết luận: M ∈ d
Bài 44 (trang 76 SGK Toán 7 tập 2): Gọi M là điểm nằm trên đường trung trực của đoạn thẳng AB, cho đoạn thẳng MA có độ dài 5cm. Hỏi độ dài MB bằng bao nhiêu?
Lời giải:
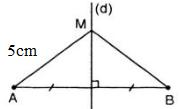
Điểm M thuộc đường trung trực của AB
=> MA = MB (định lí 1)
Vì MA = 5cm nên MB = 5cm
Bài 45 (trang 76 SGK Toán 7 tập 2): Chứng minh đường thẳng PQ được vẽ như trong hình 43 đúng là đường trung trực của đoạn thẳng MN.
Gợi ý: Sử dụng định lí 2

Hình 43
Lời giải:
Theo cách vẽ thì hai cung tròn tâm M và N có bán kính bằng nhau.
Do đó PM = PN và QM = QN
=> P, Q cách đều hai mút M, N của đoạn thẳng MN.
Áp dụng định lí 2 suy ra P, Q nằm trên đường trung trực của đoạn thẳng MN (đpcm).
Bài 46 (trang 76 SGK Toán 7 tập 2): Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chứng minh ba điểm A, D, E thẳng hàng.
Lời giải:
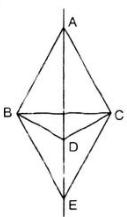
- Vì tam giác ABC cân tại A nên AB = AC. Suy ra A nằm trên đường trung trực của BC (định lí 2).
- Tương tự: điểm D và E cũng nằm trên đường trung trực của BC.
Vậy ba điểm A, D, E thẳng hàng (đpcm).
Bài 47 (trang 76 SGK Toán 7 tập 2): Cho hai điểm M, N nằm trên đường trung trực của đoạn thẳng AB. Chứng minh ΔAMN = Δ BMN.
Lời giải:
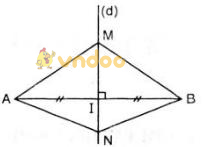
Xét ΔAMN và ΔBMN có:
- AM = MB (vì M nằm trên đường trung trực của AB)
- AN = BN (vì N nằm trên đường trung trực của AB)
- MN chung
=> ΔAMN = ΔBMN (c.c.c) (đpcm)
Bài 48 (trang 77 SGK Toán 7 tập 2): Hai điểm M và N cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.
Lời giải:
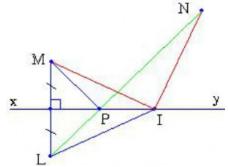
Gọi P là giao điểm của LN với xy.
- Nếu I không trùng P
Ta có: xy là đường trung trực của ML
=> IM = IL (tính chất đường trung trực của đoạn thẳng)
Xét ΔINL có IL + IN > LN (bất đẳng thức tam giác)
=> IM + IN > LN
- Nếu I ≡ P
IM + IN = IL + IN = LN
Bài 49 (trang 77 SGK Toán 7 tập 2): Hai nhà máy được xây dựng bên bờ một con sông tại hai địa điểm A và B (h.44). Hãy tìm trên bờ sông một địa điểm C để xây dựng một trạm bơm đưa nước về cho hai nhà máy sao cho độ dài đường ống dẫn nước là ngắn nhất?
Lời giải:
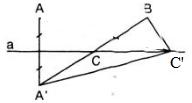
Ta có độ dài đường ống dẫn nước = CA + CB.
Gọi A' là điểm đối xứng của A qua đường thẳng a.
=> a là đường trung trực của AA' nên CA' = CA.
Do đó, CA + CB = CA' + CB
- Nếu C ≡ C' (1) (không nằm trên A'B) thì ta có:
CA + CB ≥ A'B (bất đẳng thức ΔA'C'B)
- Nếu C nằm trên A'B thì CA + CB = A'B (2)
Từ (1) và (2) ta suy ra: độ dài đường ống là ngắn nhất thì C phải là giao điểm của A'B với a.
Bài 50 (trang 77 SGK Toán 7 tập 2): Một con đường quốc lộ cách không xa hai điểm dân cư (h.45). Hãy tìm bên đường đó một địa điểm để xây dựng một trạm y tế sao cho trạm y tế này cách đều hai điểm dân cư.
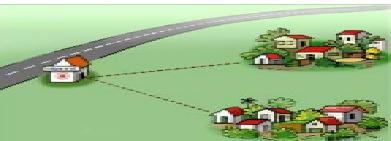
Hình 45
Lời giải:
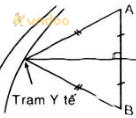
Gọi 2 điểm dân cư là hai điểm A, B. Để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường và đường trung trực của AB.
Bài 51 (trang 77 SGK Toán 7 tập 2): Cho đường thẳng d và điểm P không nằm trên d. Hình 46 minh họa cho cách dựng đường thẳng đi qua điểm P vuông góc với đường thẳng d bằng thước và compa như sau:
(1) Vẽ đường tròn tâm P với bán kính thích hợp sao cho nó có cắt d tại hai điểm A và B.
(2) Vẽ hai đường tròn với bán kính bằng nhau có tâm tại A và B sao cho chúng cắt nhau. Gọi một giao điểm của chúng là C (C ≠ P)
(3) Vẽ đường thẳng PC.
Em hãy chứng minh đường thẳng PC vuông góc với d.
Đố: Tìm thêm một cách dựng nữa (bằng thước và compa)
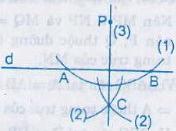
Hình 46
Lời giải:
a) A, B nằm trên cung tròn có tâm P nên PA = PB.
C là giao điểm của 2 cung bằng nhau có tâm tại A nên CA = CB.
=> P; C cách đều A và B
=> đường thẳng CP là đường trung trực của AB (định lí 2)
Do đó: PC ⊥ d
b) Một cách vẽ khác
- Lấy điểm A bất kì trên d
- Vẽ cung tròn tâm A bán kính AP cắt đường thẳng d tại M
- Vẽ cung tròn tâm M bán kính MP cắt cung tròn tâm A tại C
- Vẽ đường thẳng PC, đường thẳng PC chính là đường vuông góc với d.







