Giải bài tập SGK Toán lớp 7 bài 5: Tính chất tia phân giác của một góc
Giải bài tập Toán 7 bài 5: Tính chất tia phân giác của một góc
Giải bài tập SGK Toán lớp 7 bài 5: Tính chất tia phân giác của một góc với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán lớp 7. Lời giải hay bài tập Toán 7 này gồm các bài giải tương ứng với từng bài học trong sách giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán. Mời các bạn tham khảo
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.
Trả lời câu hỏi Toán 7 Tập 2 Bài 5 trang 68: Dựa vào cách gấp hình, hãy so sánh các khoảng cách từ điểm M đến hai cạnh Ox, Oy.
Lời giải
Khoảng cách từ M đến Ox bằng Khoảng cách từ M đến Oy
Trả lời câu hỏi Toán 7 Tập 2 Bài 5 trang 69: Dựa vào hình 29, hãy viết giả thiết và kết luận của định lí 1.
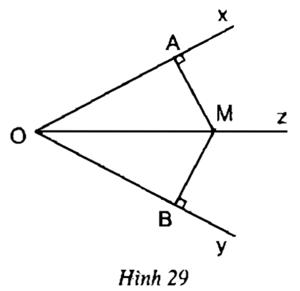
Lời giải
- Giả thiết: Góc xOy có Oz là tia phân giác
MA ⊥ Ox tại A; MB ⊥ Oy tại B
- Kết luận: MA = MB
Trả lời câu hỏi Toán 7 Tập 2 Bài 5 trang 69: Dựa vào hình 30, hãy viết giả thiết và kết luận của định lí 2.
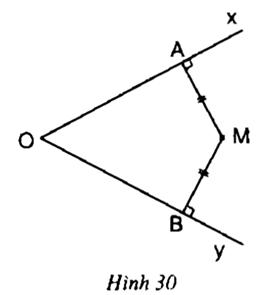
Lời giải
- Giả thiết: M nằm bên trong góc xOy
MA ⊥ Ox tại A; MB ⊥ Oy tại B
MA = MB
- Kết luận: OM là tia phân giác góc xOy
Bài 31 (trang 70 SGK Toán 7 tập 2): Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề:
Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia.
Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b.
Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy.
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy.
(Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2)
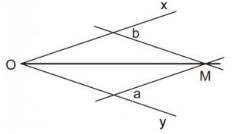
Hình 31
Lời giải
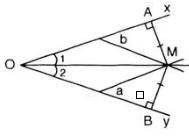
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy => MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
Bài 32 (trang 70 SGK Toán 7 tập 2): Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
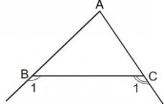
Hình 32
Lời giải:
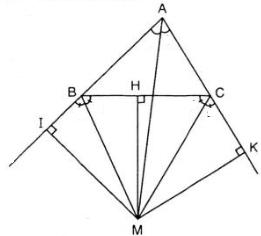
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ΔABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC
Vì M nằm trên tia phân giác của góc B1 nên MH = MI
Vì M nằm trên tia phân giác của góc C1 nên MH = MK
Suy ra: MI = MK
=> M thuộc phân giác của góc A (Định lí 2)
Bài 33 (trang 70 SGK Toán 7 tập 2): Cho hai đường thẳng xx', yy' cắt nhau tại O.
a) Chứng minh hai tia phân giác Ot, Ot' của một cặp góc kề bù tạo thành một góc vuông.
b) Chứng minh rằng: Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot' thì M cách đều hai đường thẳng xx' và yy'.
c) Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx', yy' thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot'.
d) Khi M ≡ O thì khoảng cách từ M đến xx' và yy' bằng bao nhiêu?
e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau xx', yy'.
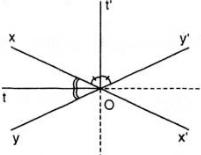
Hình 33
Lời giải
a, Vì Ot là tia phân giác của 
\(\widehat {xOy}\) nên \(\widehat {yOt} = \widehat {xOt} = \frac{1}{2}\widehat {xOy}\)
Ot' là tia phân giác của \(\widehat {xOy'}\) nên \(\widehat {y'Ot'} = \widehat {xOt'} = \frac{1}{2}\widehat {xOy'}\)
Suy ra \(\widehat {xOt} + \widehat {xOt'} = \frac{1}{2}\widehat {xOy} + \frac{1}{2}\widehat {xOy'} = \frac{1}{2}\left( {\widehat {xOy} + \widehat {xOy'}} \right)\)
Mà \(\widehat {xOy} + \widehat {xOy'} = {180^0}\) (Do hai góc kề bù)
\(\Rightarrow \widehat {xOt} + \widehat {xty'} = \frac{1}{2}{.180^0} = {90^0}\)
Vậy hai tia phân giác của hai góc kề bù tạo với nhau một góc vuông.
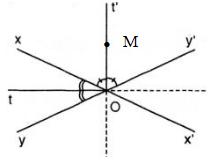
b. Nếu M ∈ Ot hoặc Ot' thì M là điểm cách đề hai đường thẳng xx', yy'
Thật vậy, giả sử M ∈ Ot
Do Ot' là phân giác của \(\widehat {xOy}\) nên M cách đều Ox, Oy'
Vậy M là điểm cách đề hai đường thẳng xx', yy'.
c. Nếu M cách đều hai đường thẳng xx', yy' và giả sử M nằm trong một góc trong bốn góc \(\widehat {xOy};\widehat {xOy'};\widehat {x'Oy'};\widehat {x'Oy}\)
Áp dụng định lí 1 thì M phải thuộc phân giác của góc ấy tức là M phải thuộc Ot hoặc Ot'
d. Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0.
e) Từ các câu trên ta có nhận xét: tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' là các đường phân giác tạo bởi các góc của hai đường thẳng đó.
Bài 34 (trang 71 SGK Toán 7 tập 2): Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
a) BC = AD;
b) IA = IC, IB = ID;
c) Tia OI là tia phân giác của góc xOy.
Lời giải:
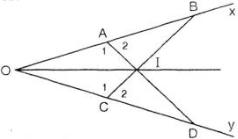
a. Xét hai tam giác OCB và tam giác OAD có:
OC = OA (gt)
Góc O là góc chung
OB = OD (gt)
Vậy ΔOCB = ΔOAD (c - g - c)
Suy ra BC = AD
b. Vì ΔOCB = ΔOAD nên \(\left\{ {\begin{array}{*{20}{c}}
{\widehat B = \widehat D} \\
{\widehat {{A_1}} = \widehat {{C_1}}}
\end{array}} \right.\)
Ta có: OA + AB = OB ⇒ AB = OB - OA = OD - OC = CD
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = {180^0} \Rightarrow \widehat {{A_2}} = {180^0} - \widehat {{A_1}} = {180^0} - \widehat {{C_1}} = \widehat {{C_2}}\)
Xét hai tam giác ΔAIB và ΔCID có:
AB = CD
\(\begin{gathered}
\widehat B = \widehat D \hfill \\
\widehat {{A_1}} = \widehat {{C_2}} \hfill \\
\end{gathered}\)
Vậy ΔAIB = ΔCID (g - c - g)
Suy ra IA = IC, IB = ID (dpcm)
c. Xét hai tam giác ΔOAI và ΔOCI có:
OA = OC
\(\widehat {{A_1}} = \widehat {{C_1}}\)
IA = IC
Vậy ΔOAI = ΔOCI (c - g - c)
\(\Rightarrow \widehat {AOI} = \widehat {COI}\)
Vậy OI là tia phân giác góc xOy
(Kí hiệu cmt là chứng minh trên)
Bài 35 (trang 71 SGK Toán 7 tập 2): 35. Có mảnh sắt phẳng hình dạng một góc (h.34) và một chiếc thước thẳng có chia khoảng. Làm thế nào để vẽ được tia phân giác của góc này?
Gợi ý: Áp dụng bài tập 34.
Hình 34
Lời giải:
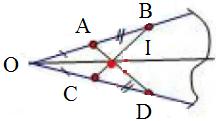
- Gọi O là giao điểm của hai đường thẳng. (Áp dụng bài 34 ta coi mảnh sắt có hình dạng như góc xoy)
- Trên cạnh thứ nhất lấy hai điểm phân biệt A, B; trên cạnh thứ hai lấy hai điểm C, D sao cho OA = OC và OB = OD.
- Gọi I là giao điểm của AD và BC. Đường thẳng OI chính là tia phân giác của góc này
Chứng minh tương tự như bài 34 (trang 71 sgk Toán 7 tập 2) để chứng minh OI là tia phân giác của góc này.
