Giải Toán 7 bài 1: Tổng ba góc của một tam giác
Giải Toán lớp 7 bài 1: Tổng ba góc của một tam giác
- Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 106
- Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 106
- Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 107
- Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 107
- Bài 1 trang 107 SGK Toán 7 Tập 1
- Bài 2 trang 108 SGK Toán 7 Tập 1
- Bài 3 trang 108 SGK Toán 7 Tập 1
- Bài 4 trang 108 SGK Toán 7 Tập 1
- Bài 7 trang 109 SGK Toán 7 Tập 1
- Bài 8 trang 109 SGK Toán 7 Tập 1
- Bài 9 trang 109 SGK Toán 7 Tập 1
Giải bài tập SGK Toán lớp 7 bài 1: Tổng ba góc của một tam giác bao gồm câu hỏi và lời giải cho các câu hỏi trong SGK Toán 7 trang 106, 107, 108 phần Hình học. Bài tập Toán 7 với lời giải chi tiết, rõ ràng dễ hiểu, tương ứng với từng bài học trong sách, giúp các bạn học sinh củng cố kiến thức, rèn luyện kỹ năng giải môn Toán lớp 7 hiệu quả. Mời các bạn tham khảo.
Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 106
Vẽ hai tam giác bất kì, dùng thước đo góc đo ba góc của mỗi tam giác rồi tính tổng số đo ba góc của mỗi tam giác.
Có nhận xét gì về các kết quả trên?
Lời giải
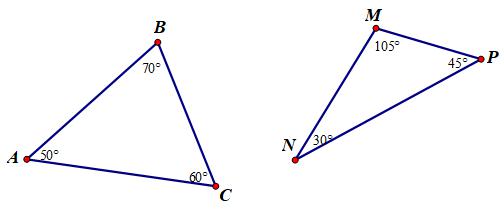
ΔABC có tổng ba góc là: 50o + 60o + 70o = 180o
ΔMNP có tổng ba góc là: 30o + 45o + 105o = 180o
Nhận xét: Tổng ba góc của hai tam giác đều là 1800
Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 106
Thực hành: Cắt một tấm bìa hình tam giác ABC. Cắt rời góc B ra rồi đặt nó kề với góc A, cắt rời góc C ra rồi đặt nó kề với góc A như hình 43. Hãy nêu dự đoán về tổng các góc A, B, C của tam giác ABC
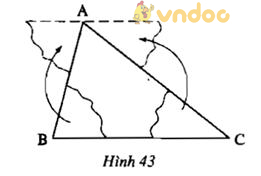
Lời giải
Dự đoán: Tổng các góc A, B, C của tam giác ABC là 180o
Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 107
Cho tam giác ABC vuông tại A. Tính tổng ∠B + ∠C
Lời giải
Tam giác ABC vuông tại A ⇒ ∠A = 90o
Lại có: Vì tổng 3 góc trong một tam giác bằng 180o
⇒ ∠B + ∠C + ∠A = 180o ⇒ ∠B + ∠C = 180o – 90o = 90o
Trả lời câu hỏi Toán 7 Tập 1 Bài 1 trang 107
Hãy điền vào các chỗ trống (…) rồi so sánh ∠(ACx) với ∠A + ∠B
Tổng ba góc của tam giác ABC bằng 1800 nên ∠A + ∠B = 180o -…
Góc ACx là góc ngoài của tam giác ABC nên ∠(ACx) = 180o -…
Lời giải
Ta có:
Tổng ba góc của tam giác ABC bằng 180o nên ∠A + ∠B = 180o - ∠C
Góc ACx là góc ngoài của tam giác ABC nên ∠(ACx) = 180o - ∠C
Do đó: ∠(ACx) = ∠A + ∠B
Bài 1 trang 107 SGK Toán 7 Tập 1
Tính các số đo x, y ở các hình 47, 48, 49, 50, 51.

Lời giải:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Trong tam giác ABC có:
y + 70o + 40o + 40o = 180o
y = 180o - 80o - 70o
y = 30o
Trong tam giác ACD có:
x + 40o + 30o = 180o
x = 180o - 40o - 30o
x = 110o
Bài 2 trang 108 SGK Toán 7 Tập 1
Cho tam giác ABC có góc B = 80o, góc C = 30o. Tia phân giác của góc A cắt BC tại D. Tính
![]()
Lời giải:
Vẽ hình:
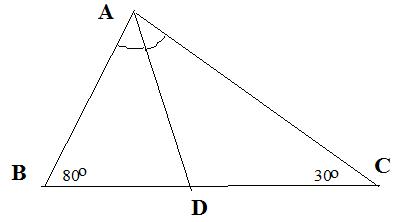
Tam giác ABC có: ![]() \(\widehat{BAC} + \widehat{B} + \widehat{C} = 180^o\) (tổng ba góc trong một tam giác)
\(\widehat{BAC} + \widehat{B} + \widehat{C} = 180^o\) (tổng ba góc trong một tam giác)
![]() \(\Rightarrow \widehat{BAC} = 180^o - (\widehat{B} + \widehat{C}) = 180^o - (80^o + 30^o) = 70^o\)
\(\Rightarrow \widehat{BAC} = 180^o - (\widehat{B} + \widehat{C}) = 180^o - (80^o + 30^o) = 70^o\)
Lại có: AD là tia phân giác của ![]() \(\widehat{BAC}\) (giả thiết)
\(\widehat{BAC}\) (giả thiết)
![]() \(\Rightarrow \widehat{BAD} = \widehat{CAD} = 70^o : 2 = 35^o\)
\(\Rightarrow \widehat{BAD} = \widehat{CAD} = 70^o : 2 = 35^o\)
Tam giác ABD có:
![]() \(\widehat{ADC} = \widehat{BAD} + \widehat{ABD} = 35^o + 80^o = 115^o\) (tính chất góc ngoài của tam giác)
\(\widehat{ADC} = \widehat{BAD} + \widehat{ABD} = 35^o + 80^o = 115^o\) (tính chất góc ngoài của tam giác)
Tam giác ADC có:
![]() \(\widehat{ADB} = \widehat{DAC} + \widehat{DCA} = 35^o + 30^o = 75^o\) (tính chất góc ngoài của tam giác)
\(\widehat{ADB} = \widehat{DAC} + \widehat{DCA} = 35^o + 30^o = 75^o\) (tính chất góc ngoài của tam giác)
Bài 3 trang 108 SGK Toán 7 Tập 1
Cho hình 52. Hãy so sánh:
a) ![]() \(\widehat{BIK}\) và
\(\widehat{BIK}\) và ![]() \(\widehat{BAK}\)
\(\widehat{BAK}\)
b) ![]() \(\widehat{BIC}\) và
\(\widehat{BIC}\) và ![]() \(\widehat{BAC}\)
\(\widehat{BAC}\)
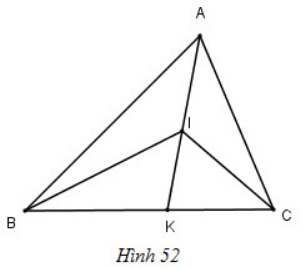
a) Ta có: ![]() \(\widehat{BIK}\) là góc ngoài của tam giác BIA
\(\widehat{BIK}\) là góc ngoài của tam giác BIA
![]() \(\Rightarrow \widehat{BIK} > \widehat{BAI}\) hay
\(\Rightarrow \widehat{BIK} > \widehat{BAI}\) hay ![]() \(\widehat{BIK} > \widehat{BAK}\) (1)
\(\widehat{BIK} > \widehat{BAK}\) (1)
b) Tương tự ta chứng mình được ![]() \(\widehat{CIK} > \widehat{CAK}\) (2)
\(\widehat{CIK} > \widehat{CAK}\) (2)
Từ (1) và (2) ![]() \(\Rightarrow \widehat{BIK} + \widehat{CIK} > \widehat{BAK} + \widehat{CAK}\)
\(\Rightarrow \widehat{BIK} + \widehat{CIK} > \widehat{BAK} + \widehat{CAK}\)
Hay ![]() \(\widehat{BIC} > \widehat{BAC}\)
\(\widehat{BIC} > \widehat{BAC}\)
Bài 4 trang 108 SGK Toán 7 Tập 1
Đố. Tháp nghiêng Pi-da ở Italia nghiêng 5o so với phương thẳng đứng (hình 58). Tính số đo của góc ABC trên hình vẽ.
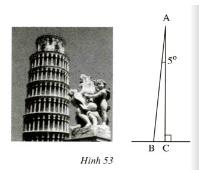
Lời giải:
Tam giác ABC vuông tại C
![]() \(\Rightarrow \widehat{A} + \widehat{B} = 90^o\)
\(\Rightarrow \widehat{A} + \widehat{B} = 90^o\)
![]() \(\Rightarrow \widehat{B} = 90^o - \widehat{A} = 90^o - 5^o = 85^o\)
\(\Rightarrow \widehat{B} = 90^o - \widehat{A} = 90^o - 5^o = 85^o\)
Bài 5 (trang 108 SGK Toán 7 Tập 1): Ta gọi tam giác có ba góc nhọn là tam giác nhọn, tam giác có một góc tù là tam giác tù. Gọi tên tam giác nhọn, tam giác tù, tam giác vuông ở hình 54.
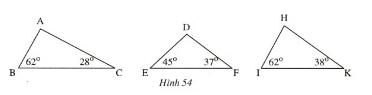
Lời giải:
+ Tam giác ABC có:
![]() \(\widehat{A} + \widehat{B} + \widehat{C} = 180^o\) (tổng ba góc trong một tam giác)
\(\widehat{A} + \widehat{B} + \widehat{C} = 180^o\) (tổng ba góc trong một tam giác)
![]() \(\Rightarrow \widehat{A} = 180^o - \widehat{B} - \widehat{C} = 180^o - 62^o - 28^o = 90^o\)
\(\Rightarrow \widehat{A} = 180^o - \widehat{B} - \widehat{C} = 180^o - 62^o - 28^o = 90^o\)
![]() \(\Rightarrow\) Tam giác ABC vuông tại A
\(\Rightarrow\) Tam giác ABC vuông tại A
+ Tam giác DEF có:
![]() \(\widehat{D} + \widehat{E} + \widehat{F} = 180^o\) (tổng ba góc trong một tam giác)
\(\widehat{D} + \widehat{E} + \widehat{F} = 180^o\) (tổng ba góc trong một tam giác)
![]() \(\Rightarrow \widehat{D} = 180^o - \widehat{E} - \widehat{F} = 180^o - 45^o - 37^o = 98^o\)
\(\Rightarrow \widehat{D} = 180^o - \widehat{E} - \widehat{F} = 180^o - 45^o - 37^o = 98^o\)
![]() \(\Rightarrow\) Tam giác DEF là tam giác tù
\(\Rightarrow\) Tam giác DEF là tam giác tù
+ Tam giác HIK có:
![]() \(\widehat{H} + \widehat{I} + \widehat{K} = 180^o\)(tổng ba góc trong một tam giác)
\(\widehat{H} + \widehat{I} + \widehat{K} = 180^o\)(tổng ba góc trong một tam giác)
![]() \(\Rightarrow \widehat{H} = 180^o - \widehat{I} - \widehat{K} = 180^o - 62^o - 38^o = 80^o\)
\(\Rightarrow \widehat{H} = 180^o - \widehat{I} - \widehat{K} = 180^o - 62^o - 38^o = 80^o\)
![]() \(\Rightarrow\) Tam giác HIK là tam giác nhọn
\(\Rightarrow\) Tam giác HIK là tam giác nhọn
Lưu ý: Tổng ba góc trong một tam giác bằng ![]() \(180^o\)
\(180^o\)
Bài 6 (trang 109 SGK Toán 7 Tập 1): Tìm số đo x ở các hình 55, 56, 57, 58.
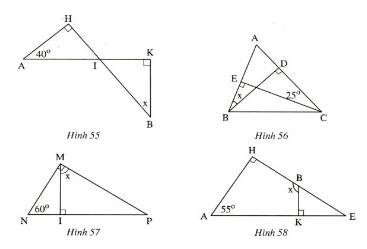
Lời giải:
+ Hình 55
ΔAHI vuông tại H (giả thiết)
![]() \(\Rightarrow \widehat{AHI} + \widehat{AIH} + \widehat{HAI} = 180^o\)(định lí tổng ba góc trong một tam giác)
\(\Rightarrow \widehat{AHI} + \widehat{AIH} + \widehat{HAI} = 180^o\)(định lí tổng ba góc trong một tam giác)
![]() \(\Rightarrow 90^o + \widehat{AIH} + 40^o = 180^o\)
\(\Rightarrow 90^o + \widehat{AIH} + 40^o = 180^o\)
![]() \(\Rightarrow \widehat{AIH} = 180^ - (90^o + 40^o)\)
\(\Rightarrow \widehat{AIH} = 180^ - (90^o + 40^o)\)
![]() \(\Rightarrow \widehat{AIH}\) =
\(\Rightarrow \widehat{AIH}\) = ![]() \(50^o\)
\(50^o\)
Lại có: ![]() \(\widehat{AIH} = \widehat{KIB}\) (cặp góc đối đỉnh)
\(\widehat{AIH} = \widehat{KIB}\) (cặp góc đối đỉnh)
![]() \(\Rightarrow \widehat{KIB} = 50^o\)
\(\Rightarrow \widehat{KIB} = 50^o\)
ΔKBI vuông tại K (giả thiết)
![]() \(\Rightarrow \widehat{KIB} + \widehat{IBK} = 90^o\) (cặp góc phụ nhau)
\(\Rightarrow \widehat{KIB} + \widehat{IBK} = 90^o\) (cặp góc phụ nhau)
![]() \(\Rightarrow \widehat{KIB} = 90^o - \widehat{IBK} = 90^o - 40^o = 50^o\)
\(\Rightarrow \widehat{KIB} = 90^o - \widehat{IBK} = 90^o - 40^o = 50^o\)
Hay ![]() \(x = 50^o\)
\(x = 50^o\)
+ Hình 56
ΔABD vuông tại D (giả thiết)
![]() \(\Rightarrow \widehat{ABD} + \widehat{ADB} + \widehat{A} = 180^o\) (định lí tổng ba góc trong một tam giác)
\(\Rightarrow \widehat{ABD} + \widehat{ADB} + \widehat{A} = 180^o\) (định lí tổng ba góc trong một tam giác)
![]() \(\Rightarrow \widehat{ABD} + 90^o + \widehat{A} = 180^o\)
\(\Rightarrow \widehat{ABD} + 90^o + \widehat{A} = 180^o\)
![]() \(\Rightarrow \widehat{ABD} + \widehat{A} = 180^o - 90^o = 90^o \,\,\,\)(1)
\(\Rightarrow \widehat{ABD} + \widehat{A} = 180^o - 90^o = 90^o \,\,\,\)(1)
Tương tự ΔACE vuông tại E (giả thiết)
![]() \(\Rightarrow \widehat{ACE} + \widehat{A} = 90^o\),(2)
\(\Rightarrow \widehat{ACE} + \widehat{A} = 90^o\),(2)
Từ (1) và (2)![]() \(\Rightarrow \widehat{ABD} = \widehat{ACE} = 25^o\)
\(\Rightarrow \widehat{ABD} = \widehat{ACE} = 25^o\)
Hay ![]() \(x = 25^o\)
\(x = 25^o\)
+ Hình 57
ΔMNI vuông tại I (giả thiết)
![]() \(\Rightarrow \widehat{N} + \widehat{NMI} + \widehat{MIN} = 180^o\)(định lí tổng ba góc trong một tam giác)
\(\Rightarrow \widehat{N} + \widehat{NMI} + \widehat{MIN} = 180^o\)(định lí tổng ba góc trong một tam giác)
![]() \(\Rightarrow 60^o + \widehat{NMI} + 90^o = 180^o\)
\(\Rightarrow 60^o + \widehat{NMI} + 90^o = 180^o\)
![]() \(\Rightarrow \widehat{NMI} = 180^o - (90^o + 60^o) = 30^o\)
\(\Rightarrow \widehat{NMI} = 180^o - (90^o + 60^o) = 30^o\)
Lại có: ![]() \(\widehat{NMI} + \widehat{IMP} = \widehat{NMP} = 90^o\)
\(\widehat{NMI} + \widehat{IMP} = \widehat{NMP} = 90^o\)
![]() \(\Rightarrow \widehat{IMP} = 90^o - \widehat{NMI} = 90^o - 30^o = 60^o\)
\(\Rightarrow \widehat{IMP} = 90^o - \widehat{NMI} = 90^o - 30^o = 60^o\)
Hay ![]() \(x = 60^o\)
\(x = 60^o\)
+ Hình 58
ΔAHE vuông tại H (giả thiết)
![]() \(\Rightarrow \widehat{A} + \widehat{E} = 90^o \,\,\,\)(1)
\(\Rightarrow \widehat{A} + \widehat{E} = 90^o \,\,\,\)(1)
ΔBKE vuông tại K (giả thiết)
![]() \(\Rightarrow \widehat{E}+ \widehat{KBE} = 90^o\),(2)
\(\Rightarrow \widehat{E}+ \widehat{KBE} = 90^o\),(2)
Từ (1) và (2) ![]() \(\Rightarrow \widehat{A} = \widehat{KBE} = 55^o\)
\(\Rightarrow \widehat{A} = \widehat{KBE} = 55^o\)
Lại có: ![]() \(\widehat{KBE} + \widehat{HBK} = 180^o\)
\(\widehat{KBE} + \widehat{HBK} = 180^o\)
![]() \(\Rightarrow \widehat{HBK} = 180^o - 55^o = 125^o\)
\(\Rightarrow \widehat{HBK} = 180^o - 55^o = 125^o\)
Hay ![]() \(x = 125^o\)
\(x = 125^o\)
Bài 7 trang 109 SGK Toán 7 Tập 1
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H ∈ BC).
a) Tìm các cặp góc phụ nhau trong hình vẽ.
b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.
Lời giải:
Vẽ hình minh họa
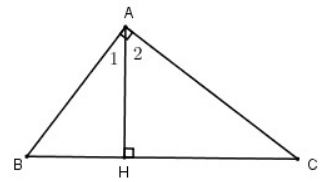
Tam giác ABC vuông tại A (giả thiết)
![]() \(\Rightarrow \widehat{B} + \widehat{C} = 90^o\)
\(\Rightarrow \widehat{B} + \widehat{C} = 90^o\)
Hay ![]() \(\widehat{B} , \, \widehat{C}\) phụ nhau
\(\widehat{B} , \, \widehat{C}\) phụ nhau
Tam giác AHB vuông tại H (giả thiết)
![]() \(\Rightarrow \widehat{B} + \widehat{A_1} = 90^o\)
\(\Rightarrow \widehat{B} + \widehat{A_1} = 90^o\)
Hay ![]() \(\widehat{B} , \, \widehat{A_1}\) phụ nhau
\(\widehat{B} , \, \widehat{A_1}\) phụ nhau
Tam giác AHC vuông tại H (giả thiết)
![]() \(\Rightarrow \widehat{A_2} + \widehat{C} = 90^o\)
\(\Rightarrow \widehat{A_2} + \widehat{C} = 90^o\)
Hay ![]() \(\widehat{A_2} , \, \widehat{C}\)phụ nhau
\(\widehat{A_2} , \, \widehat{C}\)phụ nhau
b) Ta có:
![]() \(\widehat{B} + \widehat{C} = 90^o\) (chứng minh trên)
\(\widehat{B} + \widehat{C} = 90^o\) (chứng minh trên)
![]() \(\widehat{B} + \widehat{A_1} = 90^o\) (chứng minh trên)
\(\widehat{B} + \widehat{A_1} = 90^o\) (chứng minh trên)
![]() \(\Rightarrow \widehat{A_1} = \widehat{C}\)
\(\Rightarrow \widehat{A_1} = \widehat{C}\)
![]() \(\widehat{B} + \widehat{C} = 90^o và \widehat{A_2} + \widehat{C} = 90^o\)
\(\widehat{B} + \widehat{C} = 90^o và \widehat{A_2} + \widehat{C} = 90^o\)
![]() \(\Rightarrow \widehat{A_2} = \widehat{B}\)
\(\Rightarrow \widehat{A_2} = \widehat{B}\)
Bài 8 trang 109 SGK Toán 7 Tập 1
Cho tam giác ABC có góc B = góc C = 40o. Gọi Ax là tia phân giác của góc ngoài đỉnh A. Hãy chứng tó Ax // BC.
Lời giải:
Vẽ hình minh họa
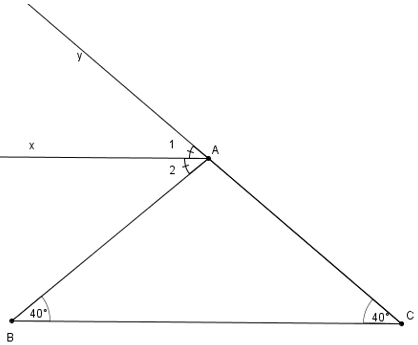
![]() \(\widehat{CAD} = \widehat{B} + \widehat{C}\) (góc ngoài của tam giác ABC)
\(\widehat{CAD} = \widehat{B} + \widehat{C}\) (góc ngoài của tam giác ABC)
![]() \(\Rightarrow \widehat{CAD} = 40^o + 40^o = 80^o\)
\(\Rightarrow \widehat{CAD} = 40^o + 40^o = 80^o\)
![]() \(\widehat{A_2} = \dfrac{1}{2}\widehat{CAD} = \dfrac{80^o}{2} = 40^o\)
\(\widehat{A_2} = \dfrac{1}{2}\widehat{CAD} = \dfrac{80^o}{2} = 40^o\)
![]() \(\Rightarrow \widehat{A_2} = \widehat{BCA}\) (vì cùng =
\(\Rightarrow \widehat{A_2} = \widehat{BCA}\) (vì cùng = ![]() \(40^o\))
\(40^o\))
Mà ![]() \(\widehat{A_2}, \, \widehat{BCA}\)là hai góc ở vị trí so le trong
\(\widehat{A_2}, \, \widehat{BCA}\)là hai góc ở vị trí so le trong ![]() \(\Rightarrow Ax // BC\)
\(\Rightarrow Ax // BC\)
Bài 9 trang 109 SGK Toán 7 Tập 1
Hình 59 biểu diễn mặt cắt ngang của một con đê. Để đo góc nhọn MOP tạo bởi một mặt phẳng nghiêng của con đê với phương nằm ngang người ta dùng thước chữ T và đặt như hình vẽ. Tính góc MOP biết rằng dây dọi BC tạo với trục BA một góc ABC = 32o
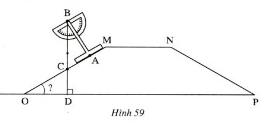
Lời giải:
Tam giác ABC vuông tại A (giả thiết)
![]() \(\Rightarrow \widehat{ABC} + \widehat{ACB} = 90^o\) (1)
\(\Rightarrow \widehat{ABC} + \widehat{ACB} = 90^o\) (1)
Tam giác OCD vuông ở D (giả thiết)
![]() \(\Rightarrow \widehat{MOP} + \widehat{OCD} = 90^o\)(2)
\(\Rightarrow \widehat{MOP} + \widehat{OCD} = 90^o\)(2)
Mặt khác ![]() \(\widehat{ACB} = \widehat{OCD}\) (hai góc đối đỉnh) (3)
\(\widehat{ACB} = \widehat{OCD}\) (hai góc đối đỉnh) (3)
Từ (1),\, (2) và (3) ![]() \(\Rightarrow \widehat{MOP} = \widehat{ABC} = 32^o\)
\(\Rightarrow \widehat{MOP} = \widehat{ABC} = 32^o\)
Tam giác ABC vuông tại A (giả thiết)
![]() \(\Rightarrow \widehat{ABC} + \widehat{ACB} = 90^o\) (1)
\(\Rightarrow \widehat{ABC} + \widehat{ACB} = 90^o\) (1)
Tam giác OCD vuông ở D (giả thiết)
![]() \(\Rightarrow \widehat{MOP} + \widehat{OCD} = 90^o\)(2)
\(\Rightarrow \widehat{MOP} + \widehat{OCD} = 90^o\)(2)
Mặt khác ![]() \(\widehat{ACB} = \widehat{OCD}\) (hai góc đối đỉnh) (3)
\(\widehat{ACB} = \widehat{OCD}\) (hai góc đối đỉnh) (3)
Từ (1),\, (2) và (3) ![]() \(\Rightarrow \widehat{MOP} = \widehat{ABC} = 32^o\)
\(\Rightarrow \widehat{MOP} = \widehat{ABC} = 32^o\)
........................
Trên đây, VnDoc đã gửi tới các bạn Giải Toán 7 bài 1: Tổng ba góc của một tam giác. Để có thể học tốt Toán 7, các em học sinh cần nắm vững lý thuyết, cũng như luyện tập giải toán để nâng cao kỹ năng giải bài tập và làm quen với nhiều dạng Toán khác nhau. Chuyên mục Giải bài tập Toán 7 được giới thiệu trên VnDoc bao gồm đáp án và hướng dẫn giải chi tiết cho từng câu hỏi trong SGK Toán 7, giúp các em làm quen với các dạng toán cơ bản, từ đó có thể vận dụng để làm các dạng toán nâng cao. Chúc các em học tốt.
- Giải bài tập SGK Toán lớp 7 bài 6: Từ vuông góc đến song song
- Giải bài tập SGK Toán lớp 7 bài 7: Định lí
- Giải bài tập SGK Toán lớp 7: Ôn tập chương I: Đường thẳng vuông góc. Đường thẳng song song
Ngoài tài liệu trên, mời các bạn tham khảo thêm: Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... cũng được cập nhật liên tục trên VnDoc.com để học tốt Toán 7 hơn.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.







