Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác
Giải Toán 7 Bài 6: Tính chất ba đường trung trực của tam giác hướng dẫn giải bài tập trong SGK Toán 7 Chân trời sáng tạo tập 2, giúp các bạn học sinh củng cố kiến thức, rèn luyện kỹ năng giải môn Toán lớp 7 hiệu quả. Mời các bạn tham khảo.
Giải Toán 7 Chân trời sáng tạo tập 2
- Khởi động trang 71 Toán 7 Tập 2:
- Khám phá 1 trang 71 Toán 7 tập 2 CTST
- Thực hành 1 trang 71 Toán 7 tập 2 CTST
- Vận dụng 1 trang 71 Toán 7 tập 2 CTST
- Khám phá 2 trang 71 Toán 7 tập 2 CTST
- Thực hành 2 trang 72 Toán 7 tập 2 CTST
- Vận dụng 2 trang 72 Toán 7 tập 2 CTST
- Bài 1 trang 72 Toán 7 tập 2 CTST
- Bài 2 trang 72 Toán 7 tập 2 CTST
- Bài 3 trang 72 Toán 7 tập 2 CTST
Khởi động trang 71 Toán 7 Tập 2:
Điểm nào cách đều ba đỉnh của một tam giác?
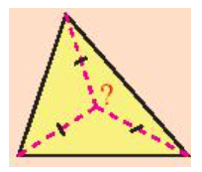
Hướng dẫn giải
Điểm cách đều ba đỉnh của một tam giác là giao điểm ba đường trung trực của tam giác đó.
Khám phá 1 trang 71 Toán 7 tập 2 CTST
Cho tam giác ABC, em hãy dùng thước kẻ và compa vẽ đường trung trực xy của cạnh BC.
Hướng dẫn giải
Để vẽ đường trung trực xy của cạnh BC ta làm như sau:
Bước 1. Xác định trung điểm của cạnh BC.
Bước 2. Qua trung điểm của cạnh BC, vẽ đường thẳng vuông góc với BC.
Bước 3. Khi đó đường thẳng vừa vẽ là đường thẳng xy.
Ta có hình vẽ sau:
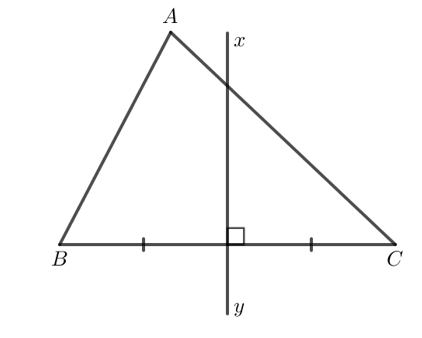
Thực hành 1 trang 71 Toán 7 tập 2 CTST
Cho tam giác nhọn ABC có M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Vẽ ba đường trung trực của tam giác ABC.
Hướng dẫn giải
Qua M vẽ đường thẳng vuông góc với BC.
Qua N vẽ đường thẳng vuông góc với CA.
Qua P vẽ đường thẳng vuông góc với AB.
Khi đó ta thu được ba đường trung trực của tam giác ABC.
Ta có hình vẽ sau:
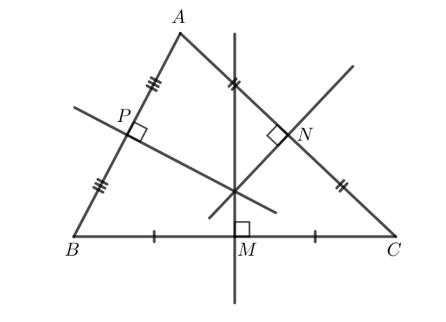
Vận dụng 1 trang 71 Toán 7 tập 2 CTST
Vẽ ba đường trung trực của tam giác ABC vuông tại A.
Hướng dẫn giải
Xác định ba điểm M, N, P lần lượt là trung điểm các cạnh BC, CA, AB.
Qua M vẽ đường thẳng vuông góc với BC.
Qua N vẽ đường thẳng vuông góc với CA.
Qua P vẽ đường thẳng vuông góc với AB.
Khi đó ta thu được ba đường trung trực của tam giác ABC.
Ta có hình vẽ sau:
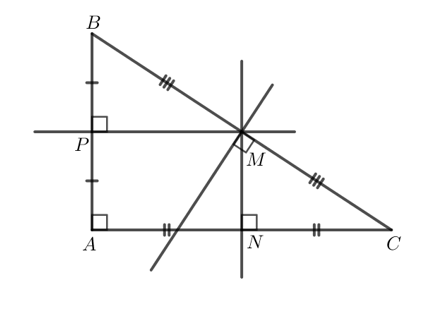
Khám phá 2 trang 71 Toán 7 tập 2 CTST
Gọi O là giao điểm của hai đường trung trực ứng với cạnh AB, AC của tam giác ABC (Hình 2).
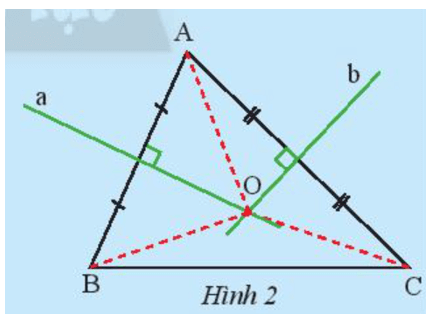
- Hãy so sánh độ dài của ba đoạn thẳng OA, OB, OC.
- Theo em, đường trung trực ứng với cạnh BC có đi qua điểm O không?
Hướng dẫn giải
- Do O nằm trên đường trung trực của AB nên OA = OB.
Do O nằm trên đường trung trực của AC nên OB = OC.
Do đó OA = OB = OC.
- Do OB = OC nên O nằm trên đường trung trực của BC.
Do đó đường trung trực ứng với cạnh BC đi qua điểm O.
Thực hành 2 trang 72 Toán 7 tập 2 CTST
Gọi O là giao điểm của ba đường trung trực của tam giác ABC (Hình 4). Hãy dùng compa vẽ đường tròn tâm O bán kính OA và cho biết đường tròn này có đi qua hai điểm B và C hay không.
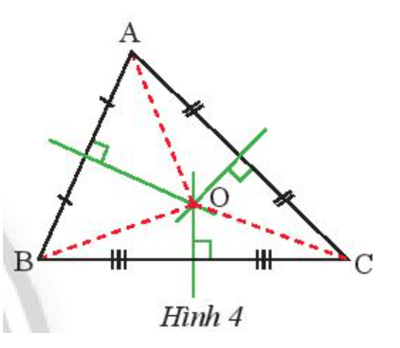
Hướng dẫn giải
Bước 1. Vẽ tam giác ABC.
Bước 2. Lần lượt chọn trung điểm của các cạnh AB, BC, CA.
Bước 3. Qua trung điểm của cạnh AB, kẻ đường thẳng vuông góc với AB.
Qua trung điểm của cạnh BC, kẻ đường thẳng vuông góc với BC.
Qua trung điểm của cạnh CA, kẻ đường thẳng vuông góc với CA.
Khi đó ta có hình vẽ sau:
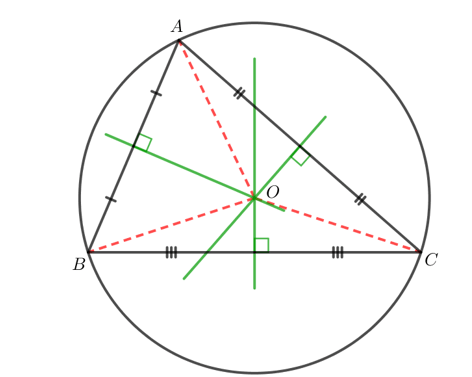
Ta thấy đường tròn tâm O bán kính OA đi qua hai điểm B và C.
Vận dụng 2 trang 72 Toán 7 tập 2 CTST
Trên bản đồ quy hoạch một khu dân cư có ba điểm dân cư A, B, C (Hình 5). Tìm địa điểm M để xây một trường học sao cho trường học này cách đều ba điểm dân cư đó.
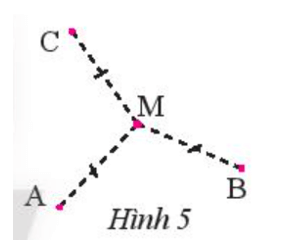
Hướng dẫn giải
Ba điểm dân cư A, B, C tạo thành ba đỉnh của tam giác ABC.
Do M cách đều ba điểm dân cư nên MA = MB = MC.
Do MA = MB nên M nằm trên đường trung trực của AB.
Do MB = MC nên M nằm trên đường trung trực của BC.
Do đó M là giao điểm ba đường trung trực của tam giác ABC.
Vậy M là giao điểm ba đường trung trực của tam giác ABC với các đỉnh là các điểm dân cư A, B, C.
Bài 1 trang 72 Toán 7 tập 2 CTST
Vẽ ba tam giác nhọn, vuông, tù
a) Xác định điểm O cách đều 3 đỉnh của mỗi tam giác.
b) Nêu nhận xét của em về vị trí điểm O trong mỗi trường hợp.
Hướng dẫn giải:
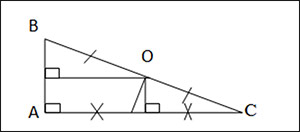
a) Tam giác vuông:
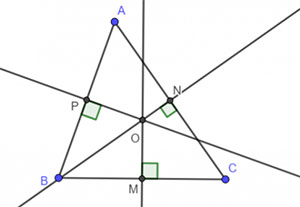
Tam giác nhọn:
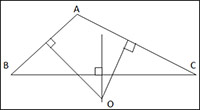
Tam giác tù:
b)
- Trong tam giác vuông: điểm O nằm trên cạnh huyền BC.
- Trong tam giác nhọn: O nằm trong tam giác ABC.
- Trong tam giác tù: O nằm ngoài tam giác ABC.
Bài 2 trang 72 Toán 7 tập 2 CTST
Cho tam giác nhọn ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA và cho O là điểm cách đều ba đỉnh của tam giác ABC. Chứng minh rằng MO vuông góc với AB, NO vuông góc với BC và PO vuông góc với AC.
Hướng dẫn giải:
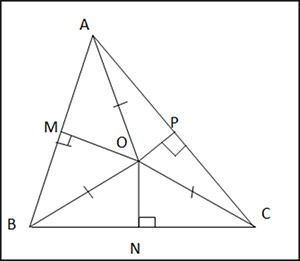
Xét ∆ MOB và ∆ MOA có:
MO chung
OB = OA
MB = MA ( M là trung điểm của AB )
=> ∆ MOB = ∆ MOA (c.c.c)
Mà
=> OM ⊥ MB hay OM ⊥ AB
Tương tự ta có: ON ⊥ NB hay ON ⊥ BC
=> O là giao điểm của 2 đường trung trực OM và ON
mà P là trung điểm của AC
=> OP là đường trung trực của AC
=> OP ⊥ AC.
Bài 3 trang 72 Toán 7 tập 2 CTST
Người ta muốn phục chế lại đĩa cổ hình tròn bị vỡ chỉ còn lại một mảnh (hình 6). Làm thế nào để xác định bán kính bị vỡ của đĩa cổ này?
Hướng dẫn giải:
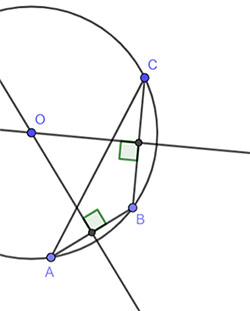
Lấy 3 điểm A, B, C bất kì thuộc cung tròn.
Xét tam giác ABC
Kẻ 2 đường trung trực của cạnh AB và BC. 2 đường trung trực cắt nhau tại điểm O
=> OA = OB = OC
=> O là tâm đường tròn qua ba điểm A, B, C.
=> OA, OB, OC là bán kính.
Vậy xác định được bán kính của đĩa cổ nãy là OA, OB, OC.
