VnDoc.com

Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến

Giải Toán 7 Chân trời sáng tạo

Bài trước

Tải về

Bài sau

Giải Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến hướng dẫn giải bài tập trong SGK Toán 7 tập 2 Chân trời sáng tạo, giúp các em học sinh ôn tập, củng cố kiến thức được học trong bài 4 chương 7 Toán 7. Sau đây mời các bạn tham khảo chi tiết.

Xem thêm

Khởi động trang 37 Toán 7 Tập 2 CTST:

Có thể nhân, chia hai đa thức một biến được không?

Hướng dẫn giải:

Ta có thể thực hiện nhân, chia hai đa thức một biến.

Khám phá 1 trang 37 Toán 7 Tập 2 CTST:

Hãy dùng tính chất phân phối để thực hiện phép nhân x . (2x + 3).

Hướng dẫn giải:

x . (2x + 3) = x . 2x + x . 3 = 2x² + 3x.

Thực hành 1 trang 37 Toán 7 Tập 2 CTST:

Thực hiện phép nhân (4x - 3)(2x² + 5x - 6).

Hướng dẫn giải:

(4x - 3)(2x² + 5x - 6)

= 4x . (2x² + 5x - 6) + (-3) . (2x² + 5x - 6)

= 4x . 2x² + 4x . 5x + 4x . (-6) + (-3) . 2x² + (-3) . 5x + (-3) . (-6)

= 8x³ + 20x² - 24x - 6x² - 15x + 18

= 8x³ + (20x² - 6x²) + (-24x - 15x) + 18

= 8x³ + 14x² - 39x + 18

Vận dụng 1 trang 37 Toán 7 Tập 2 CTST:

Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2

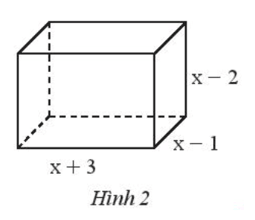
Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước

Hướng dẫn giải:

Biểu thức biểu thị thể tích của hình hộp chữ nhật trên là: (x + 3)(x - 1)(x - 2)

= [x . x + x . (-1) + 3 . x + 3 . (-1)] . (x - 2)

= (x² - x + 3x - 3) . (x - 2)

= (x² + 2x - 3) . (x - 2)

= x² . x + x² . (-2) + 2x . x + 2x . (-2) + (-3) . x + (-3) . (-2)

= x³ - 2x² + 2x² - 4x - 3x + 6

= x³ + (-2x² + 2x²) + (-4x - 3x) + 6

= x³ - 7x + 6

Vậy đa thức biểu thị thể tích của hình hộp chữ nhật trên là x³ - 7x + 6.

Khám phá 2 trang 38 Toán 7 Tập 2 CTST:

Thực hiện phép nhân (3x + 1)(x² - 2x + 1), rồi đoán xem (3x³ - 5x² + x + 1) : (3x + 1) bằng đa thức nào.

Hướng dẫn giải:

(3x + 1)(x² - 2x + 1) = 3x . (x² - 2x + 1) + 1 . (x² - 2x + 1)

= 3x . x² + 3x . (-2x) + 3x . 1 + x² - 2x + 1

= 3x³ - 6x² + 3x + x² - 2x + 1

= 3x³ + (-6x² + x²) + (3x - 2x) + 1

= 3x³ - 5x² + x + 1

Khi đó (3x³ - 5x² + x + 1) : (3x + 1) = x² - 2x + 1.

Bài 1 trang 40 Toán 7 Tập 2 CTST:

Thực hiện phép nhân

a) (4x - 3)(x + 2)

b) $(5x +2)(-x^{2} + 3x +1)$ $(5 x + 2) (- x^{2} + 3 x + 1)$

c) $(2x^{2}-7x+4)(-3x^{2}+6x+5)$ $(2 x^{2} - 7 x + 4) (- 3 x^{2} + 6 x + 5)$

Hướng dẫn giải:

a) $(4x - 3)(x + 2) = 4x(x + 2) - 3(x + 2) = 4x^{2} + 5x - 6$ $(4 x - 3) (x + 2) = 4 x (x + 2) - 3 (x + 2) = 4 x^{2} + 5 x - 6$

b) $(5x +2)(-x^{2} + 3x +1) = 5x.(-x^{2} + 3x +1) + 2(-x^{2} + 3x +1)$ $(5 x + 2) (- x^{2} + 3 x + 1) = 5 x . (- x^{2} + 3 x + 1) + 2 (- x^{2} + 3 x + 1)$

$= -5x^{3} + 13x^{2} + 11x + 2$ $= - 5 x^{3} + 13 x^{2} + 11 x + 2$

c) $(2x^{2}-7x+4)(-3x^{2}+6x+5)$ $(2 x^{2} - 7 x + 4) (- 3 x^{2} + 6 x + 5)$

$= 2x^{2}(-3x^{2}+6x+5) -7x(-3x^{2}+6x+5)+4(-3x^{2}+6x+5)$ $= 2 x^{2} (- 3 x^{2} + 6 x + 5) - 7 x (- 3 x^{2} + 6 x + 5) + 4 (- 3 x^{2} + 6 x + 5)$

$= -6x^{4}+33x^{3}-44x^{2}-11x+20$ $= - 6 x^{4} + 33 x^{3} - 44 x^{2} - 11 x + 20$

Bài 2 trang 40 Toán 7 Tập 2 CTST:

Cho hai hình chữ nhật như Hình 4. Tìm đa thức theo biến x biểu thị diện tích của phần được tô màu xanh.

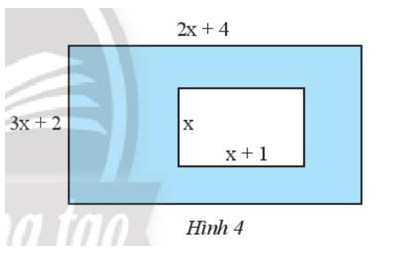
Bài 2 trang 40 Toán 7 Tập 2 Chân trời sáng tạo

Hướng dẫn giải:

Diện tích hình chữ nhật lớn là: (2x + 4)(3x + 2)

Diện tích hình chữ nhật bé là: x.(x + 1)

Diện tích phần được tô xanh là:

(2x+4)(3x+2) - x(x+1) = 2x(3x +2) + 4(3x + 2) - x(x+1) = 5x² + 15x + 8 .

Bài 3 trang 40 Toán 7 Tập 2 CTST:

Thực hiện phép chia:

a. $(8x^{6}-4x^{5}+12x^{4}-20x^{3}) : 4x^{3}$ $(8 x^{6} - 4 x^{5} + 12 x^{4} - 20 x^{3}) : 4 x^{3}$

b. $(2x^{2}-5x+3) : (2x-3)$ $(2 x^{2} - 5 x + 3) : (2 x - 3)$

Hướng dẫn giải:

a) $(8x^{6}-4x^{5}+12x^{4}-20x^{3}) : 4x^{3} = (8x^{6}-4x^{5}+12x^{4}-20x^{3}) : 4x^{3}$ $(8 x^{6} - 4 x^{5} + 12 x^{4} - 20 x^{3}) : 4 x^{3} = (8 x^{6} - 4 x^{5} + 12 x^{4} - 20 x^{3}) : 4 x^{3}$

$= (8x^{6}:4x^{3})-(4x^{5}:4x^{3})+(12x^{4}: 4x^{3})-(20x^{3}: 4x^{3})=2x^{3}-x^{2}+3x-5$ $= (8 x^{6} : 4 x^{3}) - (4 x^{5} : 4 x^{3}) + (12 x^{4} : 4 x^{3}) - (20 x^{3} : 4 x^{3}) = 2 x^{3} - x^{2} + 3 x - 5$

b)

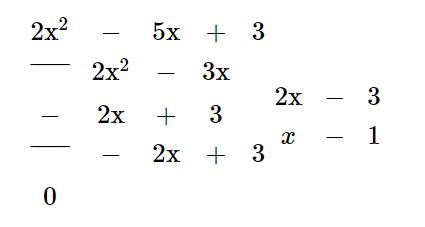
Giải Bài 3 Toán 7 tập 2 SGK trang 40

Vậy $(2x^{2}-5x+3) : (2x-3) = x - 1$ $(2 x^{2} - 5 x + 3) : (2 x - 3) = x - 1$

Bài 4 trang 40 Toán 7 Tập 2 CTST:

Thực hiện phép chia:

a. $(4x^{2}-5) : (x-2)$ $(4 x^{2} - 5) : (x - 2)$

b. $(3x^{3}-7x+2) : (2x^{2}-3)$ $(3 x^{3} - 7 x + 2) : (2 x^{2} - 3)$

Hướng dẫn giải:

a)

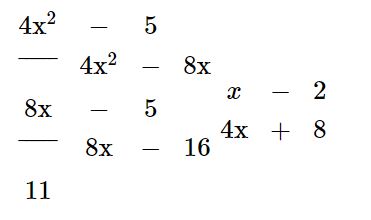
Bài 4 Toán 7 tập 2 sgk CTST

Vậy $(4x^{2}-5) : (x-2) = 4x+8$ $(4 x^{2} - 5) : (x - 2) = 4 x + 8$ dư 11.

b)

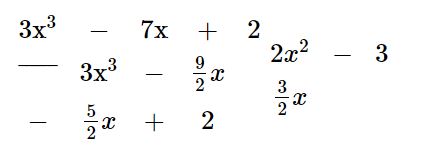
Bài 4 Toán 7 tập 2 sgk CTST

Vậy $(3x^{3}-7x+2) : (2x^{2}-3) = \frac{3}{2}x$ $(3 x^{3} - 7 x + 2) : (2 x^{2} - 3) = \frac{3}{2} x$ dư $-\frac{5}{2}x+2$ $- \frac{5}{2} x + 2$

Bài 5 trang 40 Toán 7 Tập 2 CTST:

Tính chiều dài của một hình chữ nhật có diện tích bằng $(4y^{2}+4y-3)cm^{2}$ $(4 y^{2} + 4 y - 3) c m^{2}$ và chiều rộng bằng (2y - 1) cm.

Hướng dẫn giải:

Chiều rộng của hình chữ nhật là: $(4y^{2}+4y-3): (2y-1) = (2y + 3) cm$ $(4 y^{2} + 4 y - 3) : (2 y - 1) = (2 y + 3) c m$ .

Bài 6 trang 40 Toán 7 Tập 2 CTST:

Cho hình hộp chữ nhật có thể tích bằng $3x^{3}+8x^{2}-45x-50 cm^{3}$ $3 x^{3} + 8 x^{2} - 45 x - 50 c m^{3}$ , chiều dài bằng (x+5)cm và chiều cao bằng (x+1)cm. Hãy tính chiều rộng của hình hộp chữ nhật đó.

Hướng dẫn giải:

Chiều rộng của hình hộp chữ nhật là:

$(3x^{3}+8x^{2}-45x-50):\left [ (x+5)(x+1) \right ]$ $(3 x^{3} + 8 x^{2} - 45 x - 50) : [(x + 5) (x + 1)]$

$=(3x^{3}+8x^{2}-45x-50):(x^{2}+6x+5)= 3x-10$ $= (3 x^{3} + 8 x^{2} - 45 x - 50) : (x^{2} + 6 x + 5) = 3 x - 10$

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

9

2.117

Bài trước

Bài sau

Chia sẻ bởi:
Hươu Con

Tải về

Chọn file muốn tải về:

Toán 7 Bài 4: Phép nhân và phép chia đa thức một biến

290,3 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!