Toán 7 Bài 5: Đường trung trực của một đoạn thẳng

Giải Toán 7 Bài 5: Đường trung trực của một đoạn thẳng hướng dẫn giải bài tập trong SGK Toán 7 Chân trời sáng tạo tập 2, giúp các bạn học sinh củng cố kiến thức, rèn luyện kỹ năng giải môn Toán lớp 7 hiệu quả. Mời các bạn tham khảo.

Khám phá 1 trang 67 Toán 7 tập 2 CTST

Lấy một mảnh giấy như trong Hình 1a, gọi một mép cắt là đoạn thẳng AB. Sau đó gấp mảnh giấy sao cho điểm A trùng với điểm B (Hình 1b).

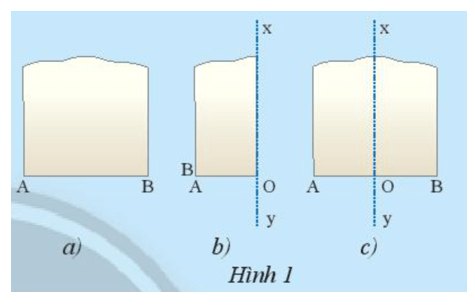
Theo em nếp gấp xy có vuông góc với đoạn AB tại trung điểm hay không? Vì sao?

Hướng dẫn giải:

Ta thấy khi gấp giấy điểm A trùng với điểm B nên O là trung điểm của AB.

Ngoài ra nếp gấp vuông góc với đoạn AB.

Do đó nếp gấp xy vuông góc với đoạn AB tại trung điểm của AB.

Thực hành 1 trang 67 Toán 7 tập 2 CTST

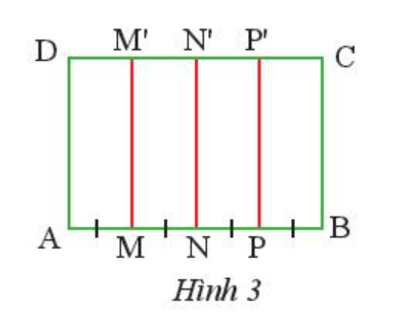
Cho hình chữ nhật ABCD, trên cạnh AB lấy các điểm M, N, P và trên cạnh DC lấy các điểm M’, N’, P’. Cho biết AM = MN = NP = PB và MM’, NN’, PP’ đều song song với BC (Hình 3). Tìm đường trung trực của mỗi đoạn thẳng AB, AN và NB.

Hướng dẫn giải:

Do ABCD là hình chữ nhật nên MM’ ⊥ AB, NN’ ⊥ AB, PP’ ⊥ AB.

Ta có AN = AM + MN; NB = NP + PB.

Do AM = MN = NP = PB nên AN = NB và N nằm giữa AB do đó N là trung điểm của AB.

Khi đó NN’ ⊥ AB và N là trung điểm của AB nên đường trung trực của đoạn AB là NN’.

Do AM = MN và M nằm giữa AN nên M là trung điểm của AN.

Do MM’ ⊥ AN và M là trung điểm của AN nên đường trung trực của đoạn AN là MM’.

Do NP = PB và P nằm giữa N và B nên P là trung điểm của NB.

Do PP’ ⊥ NB và P là trung điểm của NB nên đường trung trực của đoạn NB là PP’.

Vận dụng 1 trang 67 Toán 7 tập 2 CTST

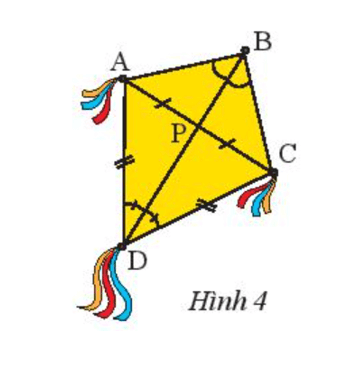
Trong Hình 4, hãy cho biết BD có là đường trung trực của đoạn thẳng AC hay không. Tại sao?

Hướng dẫn giải:

Do DA = DC (theo giả thiết) nên D nằm trên đường trung trực của đoạn thẳng AC (1).

Suy ra DP ⊥ AC.

Xét △BPA vuông tại P và △BPC vuông tại P có:

BP chung.

PA = PC (theo giả thiết).

Suy ra △BPA = △BPC (2 cạnh góc vuông).

Do đó BA = BC (2 cạnh tương ứng).

Suy ra B nằm trên đường trung trực của AC (2).

Từ (1) và (2) suy ra BD là đường trung trực của đoạn thẳng AC.

Khám phá 2 trang 68 Toán 7 tập 2 CTST

Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5).

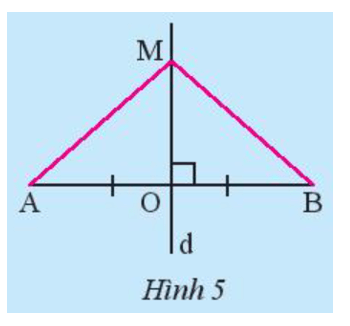
Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB.

Hướng dẫn giải:

Do d là đường trung trực của AB nên d ⊥ AB và O là trung điểm của AB.

Khi đó OA = OB.

Xét △MOA vuông tại O và △MOB vuông tại O có:

OA = OB (chứng minh trên).

OM chung.

Do đó ΔMOA = ΔMOB (2 cạnh góc vuông).

Suy ra MA = MB (2 cạnh tương ứng).

Thực hành 2 trang 69 Toán 7 tập 2 CTST

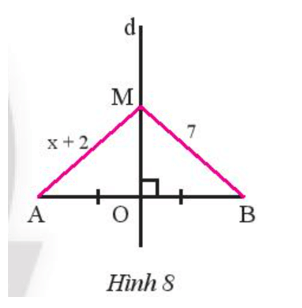
Trong Hình 8, cho biết d là đường trung trực của đoạn thẳng AB, điểm M thuộc đường thẳng d, MA = x + 2 và MB = 7. Tính x.

Hướng dẫn giải:

Do M thuộc đường trung trực của đoạn thẳng AB nên MA = MB.

Do đó x + 2 = 7 suy ra x = 5.

Vậy x = 5.

Vận dụng 2 trang 69 Toán 7 tập 2 CTST

Dựng đường trung trực của đoạn thẳng AB bằng thước thẳng và compa theo hướng dẫn sau:

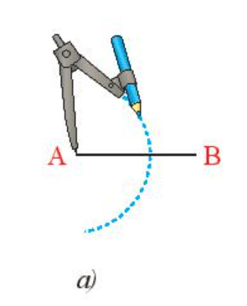
- Lấy A làm tâm vẽ cung tròn bán kính lớn hơn $\frac{1}{2}$AB (Hình 9a).

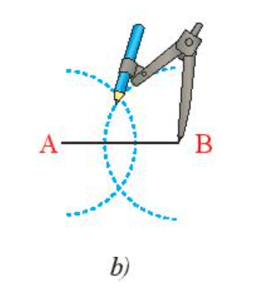
- Lấy B làm tâm vẽ cung tròn có bán kính bằng bán kính ở trên (Hình 9b).

- Hai cung tròn này cắt nhau tại M và N (Hình 9c). Dùng thước vẽ đường thẳng MN.

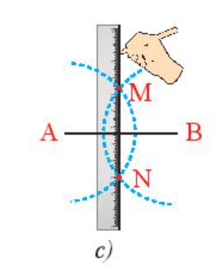
Hãy chứng minh đường thẳng MN chính là đường trung trực của đoạn thẳng AB.

Hướng dẫn giải:

Giả sử độ dài đoạn thẳng AB là 4 cm.

Thực hiện vẽ theo hướng dẫn của đề bài với bán kính cung tròn tại A và B là 3 cm.

Ta thu được hình sau:

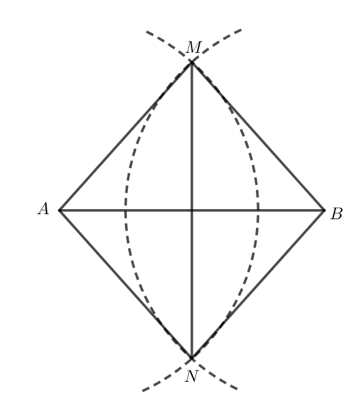
Hai cung tròn tại A và B có bán kính 3 cm cắt nhau tại M và N nên

MA = MB = NA = NB = 3 cm.

Do MA = MB nên M nằm trên đường trung trực của đoạn thẳng AB.

Do NA = NB nên N nằm trên đường trung trực của đoạn thẳng AB.

Vậy MN là đường trung trực của đoạn AB.

Bài 1 trang 70 Toán 7 tập 2 CTST

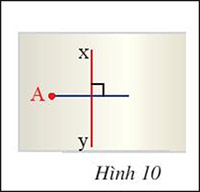
Hình 10 minh họa một tờ giấy có hình vẽ đường trung trực xy của đoạn thẳng AB mà hình ảnh điểm B bị nhòe mất. Hãy nêu cách xác định điểm B

Hướng dẫn giải:

Gọi O là giao điểm của đường trung trực xy với đoạn thẳng AB

=> O là trung điểm của AB

Lấy điểm B thuộc đường thẳng OA sao cho O là trung điểm AB.

Bài 2 trang 70 Toán 7 tập 2 CTST

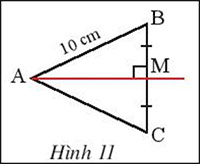
Quan sát hình 11, cho biết M là trung điểm BC, AM vuông góc với BC và AB = 10 cm. Tính AC.

Hướng dẫn giải:

M là trung điểm của BC

AM ⊥ BC

=> AM là đường trung trực của BC

=> AB = AC

=> AC =10 cm.

Bài 3 trang 70 Toán 7 tập 2 CTST

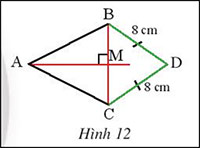
Quan sát hình 12, cho biết AM là đường trung trực của đoạn thẳng BC và DB = DC = 8 cm. Chứng minh rằng 3 điểm A, M, D thẳng hàng.

Hướng dẫn giải:

AM là đường trung trực của đoạn thẳng BC

=> AB = AC, MB = MC

Ta có DB = DC = 8 cm

=> D cách đều 2 đầu mút của đoạn thẳng AB

=> D thuộc đường trung trực của AB

=> A, M, D cùng thuộc đường trung trực của AB

=> A, M, D thẳng hàng.

Bài 4 trang 70 Toán 7 tập 2 CTST

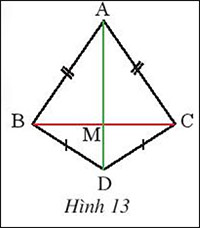
Quan sát hình 13, biết AB = AC, DB = DC. Chứng minh rằng M là trung điểm của BC

Hướng dẫn giải:

AB = AC => A thuộc đường trung trực của BC

DB= DC => D thuộc đường trung trực của BC

=> AD là đường trung trực của BC

Mà AD cắt BC tại M

=> M cũng thuộc đường trung trực AD

=> MB = MC

mà M thuộc BC

=> M là trung điểm của BC.

Bài 5 trang 70 Toán 7 tập 2 CTST

Cho hai điểm M và N nằm trên đường trung trực d của đoạn thẳng EF

Chứng minh rằng ∆EMN = ∆FMN.

Hướng dẫn giải:

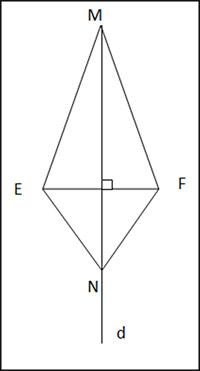
M, N thuộc đường trung trực d của đoạn thẳng EF

=> ME = MF, NE= NF

Xét ∆EMN và ∆FMN ta có:

ME = MF

NE = NF

MN chung

=> ∆EMN = ∆FMN (c.c.c)

Bài 6 trang 70 Toán 7 tập 2 CTST

Trên bản đồ quy hoạch một khu dân cư có một con đường d và hai điểm dân cư A và B (Hình 14). Hãy tìm bên đường một địa điểm M để xây dựng một trạm y tế sao cho trạm y tế cách đều hai điểm dân cư.

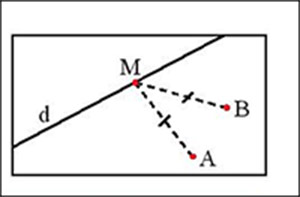
Hướng dẫn giải:

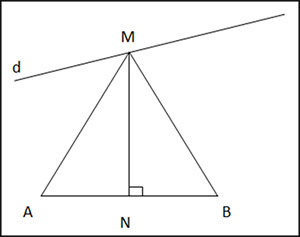
Gọi N là trung điểm của AB.

Qua N kẻ đường trung trực của đoạn thẳng AB, cắt đường thẳng d tại 1 điểm M.

=> M thuộc đường trung trực của AB

=> MA = MB

Vậy vị trí điểm M là nằm trên đường trung trực của đoạn thẳng AB.