Toán 7 Bài tập cuối chương 9 Kết nối tri thức với cuộc sống

Giải Toán 7 Bài tập cuối chương 9 sách Kết nối tri thức hướng dẫn giải bài tập trong SGK Toán 7 Kết nối tri thức tập 2 trang 84, giúp các em học sinh ôn tập, củng cố kiến thức được học, từ đó luyện giải Toán 7 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.

Bài 9.36 trang 84 SGK Toán 7 tập 2 KNTT

Cho tam giác ABC có \(\widehat{BAC}\) là một góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.

Hướng dẫn giải

Vì \(\widehat{BAC}\) là góc tù nên \(\widehat{ADE} ,\widehat{AED}\) là các góc nhọn

\(=> \widehat{DEC}\) là góc tù.

=>DC>DE (quan hệ giữa góc và cạnh đối diện trong tam giác DEC). (1)

Xét tam giác ADC có:

\(\widehat{DAC}\) là góc tù nên \(\widehat{ADC} ,\widehat{ACD}\) là các góc nhọn

\(=> \widehat{BDC}\) là góc tù.

=>BC>DC (quan hệ giữa góc và cạnh đối diện trong tam giác BDC) (2)

- Từ (1) và (2) suy ra: BC>DE

Bài 9.37 trang 84 SGK Toán 7 tập 2 KNTT

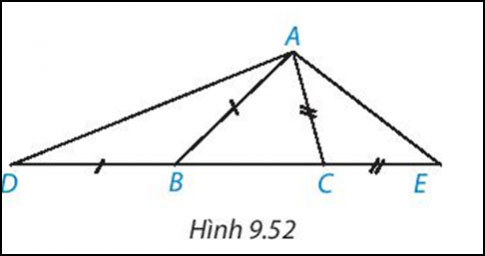
Cho tam giác ABC (AB> AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa B D và C, C nằm giữa B và E, BD = BA, CE= CA ( H.9.52)

a) So sánh \(\widehat{ADE}\) và \(\widehat{AED}\)

b) So sánh các đoạn thẳng AD và AE

Hướng dẫn giải

a) \(AB > AC => \widehat{ABC} < \widehat{ACB}\)(quan hệ giữa góc và cạnh đối diện trong tam giác ABC)

\(\widehat{ABD} + \widehat{ABC} = 180° => \widehat{ABC} = 180°- \widehat{ABD}\)

\(\widehat{ACE} + \widehat{ACB} = 180° => \widehat{ACB} = 180°- \widehat{ACE}\)

\(=> 180°- \widehat{ABD} < 180°- \widehat{ACE}\)

\(=> \widehat{ACE} < \widehat{ABD}\)

Tam giác ABD cân tại \(B ( BD= BA) => \widehat{ABD}= 180°- 2\widehat{ADB}\)

Tam giác ACE cân tại \(C ( CE= CA) => \widehat{ACE}= 180°- 2\widehat{AEC}\)

\(=> 180°- 2\widehat{ADB} > 180°- 2\widehat{AEC}\)

\(=> \widehat{ADB} < \widehat{AEC}\)

b) Xét tam giác ADE ta có: \(\widehat{ADB} < \widehat{AEC}\)

=> AD > AE

Bài 9.38 trang 84 SGK Toán 7 tập 2 KNTT

Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng

a) \(AI < \frac{1}{2} (AB + AC)\)

b) \(AM < \frac{1}{2} (AB + AC)\)

Hướng dẫn giải

a) AI là đường cao từ A xuống đoạn thẳng BC=> AI là khoảng cách từ A đến BC => AI ngắn nhất

=> AI < AB và AI < AC

Cộng 2 vế với nhau ta có: 2 AI < AB + AC

\(=> AI <\frac{1}{2} (AB + AC)\)

b) Lấy D sao cho M là trung điểm của AD

Xét ∆ ABM và ∆ DCM có

AM = DM (M là trung điểm của AD)

BM=CM (M là trung điểm của BC)

\(\widehat{AMB} = \widehat{CMD}\) (2 góc đối đỉnh)

=> ∆ ABM = ∆ DCM

=>AB = CD

Xét ∆ ADC ta có: AD < AC + CD

=> 2AM < AC + AB

\(=> AM < \frac{1}{2} (AB + AC)\)

Bài 9.39 trang 84 SGK Toán 7 tập 2 KNTT

Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A.

Gợi ý D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.

Hướng dẫn giải

C là trung điểm của AE => BC là trung tuyến của tam giác ABE (1)

D thuộc BC, BD= 2DC

\(=> BC= BD + DC = 2DC + DC = 3DC => DC = \frac{1}{3} BC (2)\)

Từ (1) và (2) => D là trọng tâm của tam giác ABE

=> AD là đường trung tuyến ứng với BE

mà AD là đường phân giác của \(\widehat{BAC}\) hay \(\widehat{BAE}\) thuộc tam giác ABE

=> Tam giác ABE cân tại A

Bài 9.40 trang 84 SGK Toán 7 tập 2 KNTT

Một sợi dây thép dài 1,2m. Cần đánh dấu trên sợi dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành một tam giác cân có một cạnh dài 30cm (H9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.

Lời giải chi tiết

TH1: Cạnh bên bằng 30 cm

Khi đó cạnh đáy bằng: 120 – (30 + 30 ) =60 (cm)

Vì 30 + 30 = 60 nên bộ 3 độ dài này không tạo được thành tam giác.

TH2: Cạnh đáy bằng 30 cm

Khi đó cạnh bên bằng: (120 – 30) : 2 = 45 (cm)

Đánh dấu AB = CD = 45 cm.