VnDoc.com

Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

Giải Toán 7 Cánh diều tập 2

Bài trước

Tải về

Bài sau

Giải Toán 7 Cánh diều Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh hướng dẫn giải bài tập trong SGK Toán 7 Cánh diều tập 2, giúp các bạn học sinh củng cố kiến thức, rèn luyện kỹ năng giải môn Toán lớp 7 hiệu quả. Mời các bạn tham khảo.

Luyện tập trang 81 Toán lớp 7 Tập 2:

Hai tam giác ở Hình 37 có bằng nhau không? Vì sao?

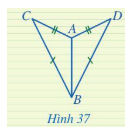
Luyện tập trang 81 Toán 7 Tập 2 Cánh diều

Hướng dẫn giải:

Xét ∆ABC và ∆ABD có:

AB chung.

BC = BD (theo giả thiết).

AC = AD (theo giả thiết).

Do đó ∆ABC = ∆ABD (c - c - c).

Hoạt động 2 trang 82 Toán lớp 7 Tập 2:

Cho hai tam giác vuông ABC và A'B'C' có: $\hat{A}$ $\hat{A}$ = $\hat{A$ $\hat{A^{'}}$ =90°, AB = A'B' = 3 cm, BC = B'C' = 5 cm (Hình 39). So sánh độ dài các cạnh AC và A'C'.

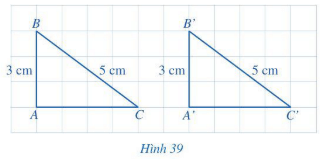
Hoạt động 2 trang 82 Toán 7 Tập 2 Cánh diều

Hướng dẫn giải:

AB và A’B’ bằng 3 lần độ dài cạnh hình vuông nhỏ.

Mà AB = A’B’ = 3 cm nên độ dài cạnh hình vuông nhỏ bằng 1 cm.

AC và A’C’ bằng 4 lần độ dài cạnh hình vuông nhỏ nên AC = A’C’ = 4 cm.

Vậy AC = A’C’.

Bài 1 trang 83 Toán lớp 7 Tập 2:

Cho Hình 42 có MN = QN, MP = QP. Chứng minh rằng $\hat{MNP}$ $\hat{M N P}$ = $\hat{QNP }$ $\hat{Q N P}$

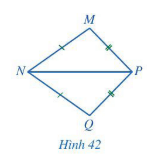
Cho Hình 42 có MN = QN, MP = QP

Hướng dẫn giải:

Xét ∆MNP và ∆QNP có:

MN = QN (theo giả thiết).

MP = QP (theo giả thiết).

NP chung.

Suy ra ∆MNP = ∆QNP(c - c - c).

Do đó $\hat{MNP}$ $\hat{M N P}$ = $\hat{QNP }$ $\hat{Q N P}$ (2 góc tương ứng).

Bài 2 trang 83 Toán lớp 7 Tập 2

Cho Hình 43 có AB = AD, $\widehat {ABC} = \widehat {ADC} = 90^\circ$ $\hat{A B C} = \hat{A D C} = 90^{\circ}$ . Chứng minh $\widehat {ACB} = \widehat {ACD}.$ $\hat{A C B} = \hat{A C D} .$

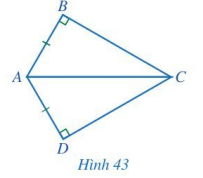
Hướng dẫn giải:

Xét hai tam giác vuông ABC và ADC có: AB = AD, AC chung.

Nên $\Delta ABC = \Delta ADC$ $Δ A B C = Δ A D C$ (cạnh huyền - cạnh góc vuông) nên $\widehat {ACB} = \widehat {ACD}$ $\hat{A C B} = \hat{A C D}$ (2 góc tương ứng)

Bài 3 trang 83 Toán lớp 7 Tập 2

Cho Hình 44 có AC = BD, $\widehat {ABC} = \widehat {BAD} = 90^\circ$ $\hat{A B C} = \hat{B A D} = 90^{\circ}$ . Chứng minh AD = BC.

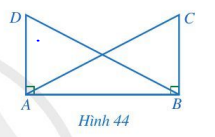
Hướng dẫn giải:

Xét hai tam giác vuông DAB và CBA: AC = BD; AB chung.

Nên $\Delta DAB = \Delta CBA$ $Δ D A B = Δ C B A$ (cạnh huyền - cạnh góc vuông)

Nên AD = BC ( 2 cạnh tương ứng)

Bài 4 trang 83 Toán lớp 7 Tập 2

Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, $\widehat A = 65^\circ$ $\hat{A} = 65^{\circ}$ , $\widehat N = 71^\circ$ $\hat{N} = 71^{\circ}$ . Tính số đo các góc còn lại của hai tam giác.

Hướng dẫn giải:

Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: $\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P.$ $\hat{A} = \hat{M}, \hat{B} = \hat{N}, \hat{C} = \hat{P} .$

Vậy $\widehat A = \widehat M = 65^\circ ; \widehat B = \widehat N = 71^\circ ; \widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ$ $\hat{A} = \hat{M} = 65^{\circ}; \hat{B} = \hat{N} = 71^{\circ}; \hat{C} = \hat{P} = 180^{\circ} - 65^{\circ} - 71^{\circ} = 44^{\circ}$ (vì tổng ba góc trong một tam giác bằng 180°).

........................

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

10

926

Bài trước

Bài sau

Chia sẻ bởi:
Điện hạ

Tải về

Chọn file muốn tải về:

Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

250 KB

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!