Toán 7 Luyện tập chung trang 37
Giải bài tập Toán 7 Kết nối tri thức
Giải Toán 7 Luyện tập chung trang 37 hướng dẫn giải bài tập trong SGK Toán 7 Kết nối tri thức trang 37, 38, giúp các em học sinh ôn tập, củng cố kiến thức, luyện giải bài tập môn Toán lớp 7. Sau đây mời các em tham khảo chi tiết.
Bài 2.19 trang 38 SGK Toán 7 tập 1
Cho các phân số: 
\(\frac{17}{80} ; \frac{611}{125} ; \frac{133}{91} ; \frac{9}{8}\)
a) Phân số nào trong những phân số trên không viết được dưới dạng số thập phân hữu hạn?
b) Cho biết \(\sqrt{2}=1,414213562\), hãy so sánh phân số tìm được trong câu a) với \(\sqrt{2}\)
Gợi ý đáp án:
a) Ta có:
\(\frac{17}{80}=0,2125\)\(\frac{611}{125}=4,888\)\(\frac{133}{91}=1,(461538)\)\(\frac{9}{8}=1,125\)
=> Số không viết được dưới dạng số thập phân hữu hạn là: \(\frac{133}{91}=1,(461538)\)
b) Ta có: \(\frac{133}{91}=1,(461538)\) mà \(1,(461538)>1,414213562=>\frac{133}{91}>\sqrt{2}\)
Bài 2.20 trang 38 SGK Toán 7 tập 1
a. Viết các phân số sau dưới dạng số thập phân vô hạn tuần hoàn (dùng dấu ngoặc để chỉ rõ chu kì):\(\frac{1}{9} ; \frac{1}{99}\). Em có nhận xét gì về kết quả nhận được?
b. Em hãy dự đoán dạng thập phân của \(\frac{1}{999}\)?
Gợi ý đáp án:
a. Viết dạng thập phân vô hạn tuần hoàn:
\(\frac{1}{9}=0,(1)\)
\(\frac{1}{99}=0,(01)\)
Nhận xét: Với phân số có dạng \(\frac{1}{9 \ldots 9}\) thì dạng thập phân vô hạn tuần hoàn của nó sẽ là 0,(00..1) với n số 9 thì có n-1 số 0
b. Dự đoán dạng thập phân của \(\frac{1}{999}=0,(001)\)
Bài 2.21 trang 38 SGK Toán 7 tập 1
Viết số \(\frac{5}{9}\) và \(\frac{5}{9}\) dưới dạng số thập phân vô hạn tuần hoàn.
Gợi ý đáp án:\(\begin{aligned}
&\frac{5}{9}=0,(5) \\
&\frac{5}{9}=0,(05)
\end{aligned}\)
Bài 2.22 trang 38 SGK Toán 7 tập 1
Nam vẽ một phần trục số trên vở ô li và đánh dấu ba điểm A, B,C như sau:
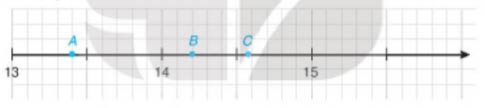
a. Hãy cho biết hai điểm A,B biểu diễn những số thập phân nào?
b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05.
Gợi ý đáp án:
a. Điểm A, B biểu diễn những số thập phân sau:
- Điểm A biểu diễn số 13,4
- Điểm B biểu diễn số 14,2
b. Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05, ta được 14,6.
Bài 2.23 trang 38 SGK Toán 7 tập 1
Thay dấu “?” bằng chữ số thích hợp.
a) -7,02 < -7, ? (1);
b) -15,3 ? 021 < -15,3819
Gợi ý đáp án:
a) -7,02 < -7,0 (1);
b) -15,39021 < -15,3819
Bài 2.24 trang 38 SGK Toán 7 tập 1
So sánh:
a. 12,26 và 12,(24);
b. 31,3(5) và 29,9(8)
Gợi ý đáp án:
a) Làm tròn kết quả với độ chính xác 0,005 được 12(24) = 12,242424... ≈ 12,24.
Mà 12,26 > 12,24 nên 12,26 > 12,(24).
b) Vì 31 > 29 nên 31,3(5) > 29,9(8).
Vậy 31,3(5) > 29,9(8).
Bài 2.25 trang 38 SGK Toán 7 tập 1
Tính:
a.\(\sqrt{1}\)
b. \(\sqrt{1 + 2 + 1}\)
c. \(\sqrt{1 + 2 + 3 + 2+ 1}\)
Gợi ý đáp án:
a. \(\sqrt{1} = 1\)
b. \(\sqrt{1 + 2 + 1} = \sqrt{4} = 2\)
c. \(\sqrt{1 + 2 + 3 + 2+ 1} = \sqrt{9}= 3\)
Bài 2.26 trang 38 SGK Toán 7 tập 1
Tính:
a. \(\left ( \sqrt{3} \right )^{2}\)
b. \(\left ( \sqrt{21} \right )^{2}\)
Gợi ý đáp án:
a. \(\left ( \sqrt{3} \right )^{2} = \sqrt{3}\)
b. \(\left ( \sqrt{21} \right )^{2} = \sqrt{21}\)
