Toán 7 Luyện tập chung trang 14
Giải Toán 7 trang 14, 15 Kết nối tri thức với cuộc sống
Giải Toán 7 Luyện tập chung trang 14, 15 sách Kết nối tri thức hướng dẫn giải bài tập trong SGK Toán 7 Kết nối tri thức tập 1, giúp các em ôn tập, củng cố kiến thức, luyện tập Giải Toán 7 Kết nối tri thức.
Bài 1.12 trang 14 SGK Toán 7 tập 1 KNTT
So sánh:
a) 
\(\frac{{123}}{7}\) và 17,75
b) \(- \frac{{65}}{9}\) và -7,125
Hướng dẫn giải:
a) \(\frac{{123}}{7}\) và 17,75
Ta có:
\(\begin{matrix}
17,75 = \dfrac{{1775}}{{100}} = \dfrac{{71}}{4} = \dfrac{{71.7}}{{4.7}} = \dfrac{{497}}{{28}} \hfill \\
\dfrac{{123}}{7} = \dfrac{{123.4}}{{7.4}} = \dfrac{{492}}{{28}} \hfill \\
\end{matrix}\)
Do 497 > 492 => \(\frac{{497}}{{28}} > \frac{{492}}{{28}}\)
Vậy \(17,75 > \frac{{123}}{7}\)
b) \(- \frac{{65}}{9}\) và -7,125
Ta có:
\(\begin{matrix}
- 7,125 = \dfrac{{ - 7125}}{{1000}} = - \dfrac{{57}}{8} = - \dfrac{{513}}{{72}} \hfill \\
- \dfrac{{65}}{9} = - \dfrac{{65.8}}{{9.8}} = - \dfrac{{520}}{{72}} \hfill \\
\end{matrix}\)
Do 520 > 513 => -520 < -513
=> \(- \frac{{520}}{{72}} < - \frac{{513}}{{72}}\)
Vậy \(- \frac{{65}}{9} < - 7,125\)
Bài 1.13 trang 15 SGK Toán 7 tập 1 KNTT
|
Khí hiếm |
Điểm đông đặc (oC) |
Điểm sôi (oC) |
|
Argon (A – gon) |
–189,2 |
–185,7 |
|
Helium (Hê – li) |
–272,2 |
–268,6 |
|
Neon (Nê – on) |
–248,67 |
–245,72 |
|
Krypton (Kríp – tôn) |
–156,6 |
–152,3 |
|
Radon (Ra – đôn) |
–71,0 |
–61,8 |
|
Xenon (Xê – nôn) |
–111,9 |
–107,1 |
(Theo britannica.com)
a) Khí hiếm nào có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton?
b) Khí hiếm nào có điểm sôi lớn hơn điểm sôi của Argon?
c) Hãy sắp xếp các khí hiếm theo thứ tự điểm đông đặc tăng dần;
d) Hãy sắp xếp các khí hiếm theo thứ tự điểm sôi giảm dần.
Hướng dẫn giải:
a) Do –156,6 > –189,2 > –248,67 > –272,2 nên khí hiếm có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton là: Argon, Neon, Helium.
Vậy khí hiếm có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton là: Argon, Neon, Helium.
b) Do –61,8 > –107,1 > –152,3 > –185,7 nên khí hiếm có điểm sôi lớn hơn điểm sôi của Argon là: Radon, Xenon, Krypton.
Vậy khí hiếm có điểm sôi lớn hơn điểm sôi của Argon là: Radon, Xenon, Krypton.
c) Do –272,2 < –248,67 < –189,2 < –156,6 < –111,9 < –71,0 nên các khí hiếm sắp xếp theo thứ tự đông đặc tăng dần là: Helium, Neon, Argon, Krypton, Xenon, Radon.
Vậy khí hiếm sắp xếp theo thứ tự đông đặc tăng dần là: Helium, Neon, Argon, Krypton, Xenon, Radon.
d) Do –61,8 > –107,1 > –152,3 > –185,7 > –245,72 > –268,6 nên các khí hiếm sắp xếp theo thứ tự điểm sôi giảm dần là: Radon, Xenon, Krypton, Argon, Neon, Helium.
Vậy các khí hiếm sắp xếp theo thứ tự điểm sôi giảm dần là: Radon, Xenon, Krypton, Argon, Neon, Helium.
Bài 1.14 trang 15 SGK Toán 7 tập 1 KNTT
Theo Đài khí tượng thủy văn tỉnh Lào Cai, ngày 10 – 01 – 2021, nhiệt độ thấp nhất tại thị xã Sa Pa là – 0,70C; nhiệt độ tại thành phố Lào Cai là 9,60C. Hỏi nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa bao nhiêu độ C?
(Theo vietnamplus.vn)
Hướng dẫn giải:
Nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa là:
9,6 – (– 0,7) = 9,6 + 0,7 = 10,3 (oC)
Vậy nhiệt độ tại thành phố Lào Cai cao hơn 10,3 oC so với nhiệt độ tại thị xã Sa Pa.
Bài 1.15 trang 15 SGK Toán 7 tập 1 KNTT
Thay mỗi dấu “?” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.11, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.
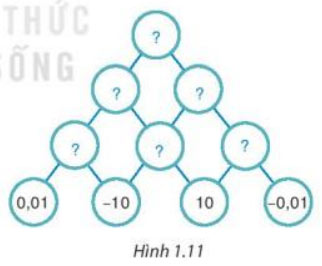
Hướng dẫn giải:
Đặt các ô lần lượt là a, b, c, d, e, f như hình sau:
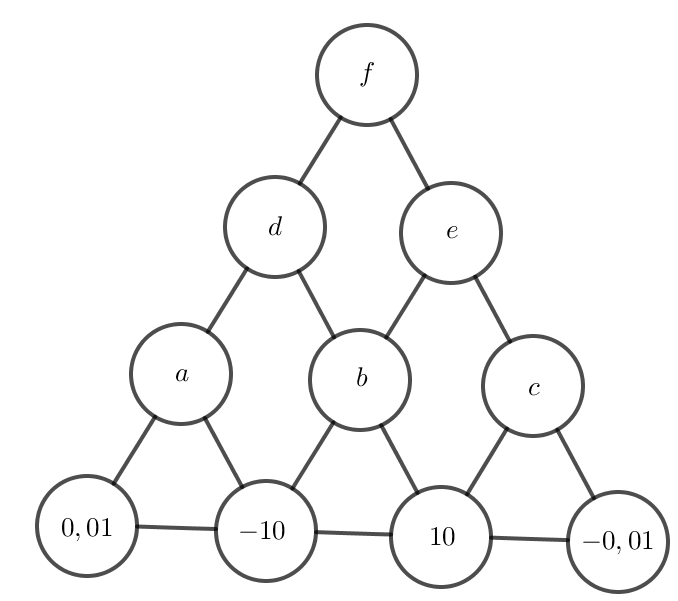
Áp dụng quy tắc của đề bài, ta tính được: a = 0,01.(–10) = –0,1;
b = (–10).10 = –100;
c = 10.( –0,01) = –0,1;
d = a.b = (–0,1).( –100) = 10;
e = b.c = (–100).( –0,1) = 10;
cf = d.e = 10.10 = 100.
Khi đó ta có bảng sau:
Bài 1.16 trang 15 SGK Toán 7 tập 1 KNTT
Tính giá trị của các biểu thức sau:
a) \(A = \left( {2 - \frac{1}{2} - \frac{1}{8}} \right):\left( {1 - \frac{3}{2} - \frac{3}{4}} \right)\)
b) \(B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}\)
Hướng dẫn giải:
Thực hiện phép tính ta có:
a) \(A = \left( {2 - \frac{1}{2} - \frac{1}{8}} \right):\left( {1 - \frac{3}{2} - \frac{3}{4}} \right)\)
\(A = \left( {\frac{{16}}{8} - \frac{4}{8} - \frac{1}{8}} \right):\left( {\frac{4}{4} - \frac{6}{4} - \frac{3}{4}} \right)\)
\(A = \frac{{11}}{8}:\frac{{ - 5}}{4}\)
\(A = \frac{{11}}{8}.\frac{4}{{ - 5}} = \frac{{11}}{{ - 10}}\)
b) \(B = 5 - \dfrac{{1 + \dfrac{1}{3}}}{{1 - \dfrac{1}{3}}}\)
\(B = 5 - \dfrac{{\dfrac{3}{3} + \dfrac{1}{3}}}{{\dfrac{3}{3} - \dfrac{1}{3}}}\)
\(B = 5 - \frac{4}{3}:\frac{2}{3}\)
\(B = 5 - \frac{4}{3}.\frac{3}{2}\)
\(B = 5 - 2 = 3\)
Bài 1.17 trang 15 SGK Toán 7 tập 1 KNTT
Tính một cách hợp lí
\(1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - 1,2.5\frac{3}{4} - \frac{{16}}{7}.\frac{{ - 71}}{8}\)
Hướng dẫn giải:
Thực hiện phép tính như sau:
\(1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - 1,2.5\frac{3}{4} - \frac{{16}}{7}.\frac{{ - 71}}{8}\)
\(= 1,2.\frac{{15}}{4} - 1,2.\frac{{23}}{4} + \frac{{16}}{7}.\frac{{ - 85}}{8} - \frac{{16}}{7}.\frac{{ - 71}}{8}\)
\(= 1,2.\left( {\frac{{15}}{4} - \frac{{23}}{4}} \right) + \frac{{16}}{7}.\left( {\frac{{ - 85}}{8} - \frac{{ - 71}}{8}} \right)\)
\(= 1,2.\frac{{ - 8}}{4} + \frac{{16}}{7}.\frac{{ - 14}}{8}\)
\(= - 2,4 + \left( { - 4} \right) = - 6,4\)
