Toán 7 Bài 27: Phép nhân đa thức một biến

Giải Toán 7 Bài 27: Phép nhân đa thức một biến sách Kết nối tri thức hướng dẫn giải bài tập trong SGK Toán 7 Kết nối tri thức tập 2 trang 36, 37, 38, giúp các em học sinh ôn tập, củng cố kiến thức được học trong bài 27 Toán 7. Sau đây mời các bạn tham khảo chi tiết. 

Mở đầu trang 36 Toán 7 Tập 2:

Anh Pi: Em hãy:

- Lấy tuổi của mình cộng với 1 rồi bình phương lên. Số nhận được gọi là kết quả thứ nhất.

- Lại lấy tuổi của mình trừ đi 1 rồi bình phương lên. Số nhận được gọi là kết quả thứ hai.

- Lấy kết quả thứ nhất trừ đi kết quả thứ hai và cho anh biết kết quả cuối cùng.

Anh sẽ đoán được tuổi của em.

Không biết anh Pi làm thế nào nhỉ? Học xong bài này em sẽ khám phá được bí mật đó.

Hướng dẫn giải:

Giả sử kết quả cuối cùng là 48.

Gọi tuổi cần đoán là x tuổi (x ∈ N *).

Lấy tuổi cộng 1 rồi bình phương lên ta được (x + 1)².

Ta có (x + 1)² = (x + 1).(x + 1) = x.(x + 1) + 1.(x + 1)

= x.x + x.1 + 1.x + 1.1

= x¹⁺¹ + x + x + 1

= x² + 2x + 1

Lấy tuổi trừ 1 rồi bình phương lên ta được (x - 1)².

Ta có (x - 1)² = (x - 1).(x - 1) = x.(x - 1) - 1.(x - 1)

= x[x + (-1)] - (x - 1)

= x.x + x.(-1) - x + 1

= x¹⁺¹ + (-x) - x + 1

= x² - x - x + 1

= x² - 2x + 1

Lấy kết quả thứ nhất trừ đi kết quả thứ hai ta được:

(x² + 2x + 1) - (x² - 2x + 1)

= x² + 2x + 1 - x² + 2x - 1

= (x² - x²) + (2x + 2x) + (1 - 1)

= 4x

Do kết quả cuối cùng là 48 nên 4x = 48

x = 48 : 4

x = 12.

Vậy tuổi cần đoán là 12.

Hoạt động 1 trang 36 SGK Toán 7 tập 2 KNTT

Hãy nhắc lại cách nhân hai đơn thức và tính (12x³) . (-5x²).

Hướng dẫn giải:

Cách nhân hai đơn thức: Để nhân hai đơn thức tùy ý, ta thực hiện nhân hai hệ số với nhau và nhân hai lũy thừa của biến với nhau.

(12x³) . (-5x²) = [12 . (-5)] . (x³ . x²) = -60.(x^{3 + 2}) = -60x⁵.

Hoạt động 2 trang 36 SGK Toán 7 tập 2 KNTT

Áp dụng tính chất phân phối của phép nhân đối với phép cộng, hãy tìm tích 2x . (3x² - 8x + 1). bằng cách nhân 2x với từng hạng tử của đa thức 3x² - 8x + 1 rồi cộng các tích tìm được.

Hướng dẫn giải:

3x² - 8x + 1 = 3x² + (-8x) + 1.

Nhân 2x với 3x² ta được 2x . 3x² = (2 . 3) . (x . x²) = 6.x¹⁺² = 6x³.

Nhân 2x với -8x ta được: 2x . (-8x) = [2.(-8)] . (x . x) = -16x¹⁺¹ = -16x².

Nhân 2x với 1 ta được: 2x.1 = 2x.

Cộng các tích ta được 6x³ + (-16x²) + 2x = 6x³ - 16x² + 2x.

Hoạt động 3 trang 37 SGK Toán 7 tập 2 KNTT

Tính (2x - 3) . (x² - 5x + 1) bằng cách thực hiện các bước sau:

Bước 1. Nhân 2x với đa thức x² - 5x + 1.

Bước 2. Nhân -3 với đa thức x² - 5x + 1.

Bước 3. Cộng các đa thức thu được ở hai bước trên và thu gọn.

Kết quả thu được là tích của đa thức 2x - 3 với đa thức x² - 5x + 1.

Hướng dẫn giải:

Nhân 2x với đa thức x² - 5x + 1 ta được:

2x . (x² - 5x + 1) = 2x.x² + 2x.(-5x) + 2x.1 = 2x³ -10x² + 2x.

Nhân -3 với đa thức x² - 5x + 1 ta được:

-3(x² - 5x + 1) = -3.x² + (-3).(-5x) + (-3.1) = -3x² + 15x + (-3) = -3x² + 15x - 3.

Cộng các đa thức trên ta được:

(2x³ -10x² + 2x) + (-3x² + 15x - 3)

= 2x³ -10x² + 2x - 3x² + 15x - 3

= 2x³ + (-10x² - 3x²) + (2x + 15x) - 3

= 2x³ + (-13x²) + 17x - 3

= 2x³ - 13x² + 17x - 3

Vậy (2x - 3) . (x² - 5x + 1) = 2x³ - 13x² + 17x - 3.

Luyện tập 2 trang 38 Toán 7 Tập 2:

Tính (x³ - 2x² + x -1)(3x - 2). Trình bày lời giải theo hai cách

Hướng dẫn giải:

Cách 1. Bỏ dấu ngoặc ta được:

(x³ - 2x² + x -1)(3x - 2)

= x³(3x - 2) + (-2x²).(3x - 2) + x.(3x - 2) + (-1)(3x - 2)

= x³.3x + x³.(-2) + (-2x²).3x + (-2x²).(-2) + x.3x + x.(-2) + (-1).3x + (-1).(-2)

= 3x⁴ + (-2x³) + (-6x³) + 4x² + 3x² + (-2x) + (-3x) + 2

= 3x⁴ + (-8x³) + 7x² + (-5x) + 2

= 3x⁴ - 8x³ + 7x² - 5x + 2

Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Cách 2. Đặt phép tính ta được:

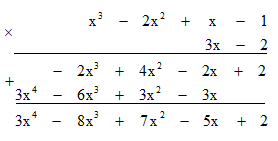
Vậy (x³ - 2x² + x -1)(3x - 2) = 3x⁴ - 8x³ + 7x² - 5x + 2.

Vận dụng 2 trang 38 SGK Toán 7 tập 2 KNTT

Rút gọn biểu thức (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x).

Hướng dẫn giải:

Xét (x - 2)(2x³ - x² + 1) = x(2x³ - x² + 1) + (-2).(2x³ - x² + 1)

= x.2x³ + x.(-x²) + x.1 + (-2).2x³ + (-2).(-x²) + (-2).1

= 2x⁴ + (-x³) + x + (-4x³) + 2x² + (-2)

= 2x⁴ - x³ + x - 4x³ + 2x² - 2

= 2x⁴ + (-x³ - 4x³) + 2x² + x - 2

= 2x⁴ + (-5x³) + 2x² + x - 2

= 2x⁴ - 5x³ + 2x² + x - 2

Xét (x - 2)x²(1 - 2x) = (x - 2)[x².1 + x²(-2x)]

= (x - 2)[x² + (-2x³)]

= x[x² + (-2x³)] + (-2).[x² + (-2x³)]

= x.x² + x.(-2x³) + (-2)x² + (-2).(-2x³)

= x³ + (-2x⁴) - 2x² + 4x³

= x³ - 2x⁴ - 2x² + 4x³

= -2x⁴ + (x³ + 4x³) - 2x²

= -2x⁴ + 5x³ - 2x²

Do đó (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x)

= (2x⁴ - 5x³ + 2x² + x - 2) + (-2x⁴ + 5x³ - 2x²)

= 2x⁴ - 5x³ + 2x² + x - 2 -2x⁴ + 5x³ - 2x²

= (2x⁴ - 2x⁴) + (- 5x³ + 5x³) + (2x² - 2x²) + x - 2

= x - 2.

Vậy (x - 2)(2x³ - x² + 1) + (x - 2)x²(1 - 2x) = x - 2.

Vận dụng 3 trang 38 SGK Toán 7 tập 2 KNTT

Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau:

- Gọi x là tuổi cần đoán. Tìm hai đa thức (biến x) biểu thị kết quả thứ nhất và kết quả thứ hai.

- Tìm đa thức biểu thị kết quả cuối cùng.

Từ đó hãy nêu cách tìm x.

Hướng dẫn giải:

Gọi tuổi cần đoán là x tuổi (x ∈ N * ).

Lấy tuổi cộng 1 rồi bình phương lên ta được (x + 1)².

Ta có (x + 1)² = (x + 1).(x + 1) = x.(x + 1) + 1.(x + 1)

= x.x + x.1 + 1.x + 1.1

= x¹⁺¹ + x + x + 1

= x² + 2x + 1

Lấy tuổi trừ 1 rồi bình phương lên ta được (x - 1)².

Ta có (x - 1)² = (x - 1).(x - 1) = x.(x - 1) - 1.(x - 1)

= x[x + (-1)] - (x - 1)

= x.x + x.(-1) - x + 1

= x¹⁺¹ + (-x) - x + 1

= x² - x - x + 1

= x² - 2x + 1

Lấy kết quả thứ nhất trừ đi kết quả thứ hai ta được:

(x² + 2x + 1) - (x² - 2x + 1)

= x² + 2x + 1 - x² + 2x - 1

= (x² - x²) + (2x + 2x) + (1 - 1)

= 4x

Khi đó kết quả cuối cùng là 4x.

Để tìm ra số tuổi cần đoán, ta lấy kết quả cuối cùng chia 4.

Bài 7.23 trang 38 SGK Toán 7 tập 2 KNTT

Thực hiện các phép tính sau:

a) \(6x^2 . (2x^3 – 3x^2 + 5x – 4)\);

b) \((-1,2x^2) . (2,5x^4 – 2x^3 + x^2 – 1,5)\).

Hướng dẫn giải:

a) \(6x^2 . (2x^3 – 3x^2 + 5x – 4)\)

\(= 6x^2 . 2x^3 + 6x^2 . (-3x^2) + 6x^2 . 5x + 6x^2 . (-4)\)

\(= 12x^5 – 18x^4 + 30x^3 – 24x^2\)

b) \((-1,2x^2) . (2,5x^4 – 2x^3 + x^2 – 1,5)\)

\(= (-1,2x^2) . 2,5x^4 + (-1,2x^2). (-2x^3) + (-1,2x^2) . x^2 + (-1,2x^2) . (-1,5)\)

\(= -3x^6 + 2,4x^5 – 1,2x^4 + 1,8x^2\)

Bài 7.24 trang 38 SGK Toán 7 tập 2 KNTT

Rút gọn các biểu thức sau:

a) \(4x^2(5x^2 + 3) – 6x(3x^3 – 2x + 1) – 5x^3(2x – 1)\);

b) \(\frac{3}{2}x(x^2 - \frac{2}{3}x + 2) - \frac{5}{3}x^2(x + \frac{6}{5})\)

Hướng dẫn giải:

a) \(4x^2(5x^2 + 3) – 6x(3x^3 – 2x + 1) – 5x^3(2x – 1)\);

\(= 4x^2. 5x^2 + 4x^2 . 3 + (-6x). 3x^3 + (-6x).(-2x) + (-6x).1 + (-5x^3).2x + (-5x^3). (-1)\)

\(= 20x^4 + 12x^2 – 18x^4 + 12x^2 – 6x – 10x^4 + 5x^3\)

\(= -8x^4 + 5x^3 + 24x^2 – 6x\)

b) \(\frac{3}{2}x(x^2 - \frac{2}{3}x + 2) - \frac{5}{3}x^2(x + \frac{6}{5})\)

\(= \frac{3}{2}x . x^2 + \frac{3}{2}x . (- \frac{2}{3}x) + \frac{3}{2}x . 2 + (-\frac{5}{3}x^2). x + (-\frac{5}{3}x^2) . \frac{6}{5})\)

\(= \frac{3}{2}x^3 – x^2 + 3x -\frac{5}{3}x^3 - 2x^2\)

\(= -\frac{1}{6}x^3 – 3x^2 + 3x\)

Bài 7.25 trang 38 SGK Toán 7 tập 2 KNTT

Thực hiện các phép nhân sau:

a) \((x^2 – x) . (2x^2 – x – 10)\);

b) \((0,2x^2 – 3x) . 5(x^2 – 7x + 3)\).

Hướng dẫn giải:

a) \((x^2 – x) . (2x^2 – x – 10)\)

\(= x^2 . 2x^2 + x^2 . (-x) + x^2 . (-10) + (-x) . 2x^2 + (-x). (-x) + (-x) . (-10)\)

\(= 2x^4 – x^3 – 10x^2 – 2x^3 + x^2 + 10x\)

\(= 2x^4 – 3x^3 – 9x^2 + 10x\)

b) \((0,2x^2 – 3x) . 5(x^2 – 7x + 3)\)

\(= (0,2x^2 – 3x) . (5x^2 – 35x + 15)\)

\(= 0,2x^2 . 5x^2 + 0,2x^2 . (-35x) + 0,2x^2 . 15 + (-3x) . 5x^2 + (-3x) . (-35x)+ (-3x) . 15\)

\(= x^4 – 7x^3 + 3x^2 – 15x^3 + 105x^2 – 45x\)

\(= x^4 – 22x^3 + 108x^2 – 45x\)

Bài 7.26 trang 38 SGK Toán 7 tập 2 KNTT

a) Tính \((x^2 – 2x + 5) . (x – 2)\).

b) Từ đó hãy suy ra kết quả của phép nhân \((x^2 – 2x + 5) . (2 – x)\). Giải thích cách làm.

Hướng dẫn giải:

a) \((x^2 – 2x + 5) . (x – 2)\)

\(= x^2.x + x^2 . (-2) + (-2x) . x + (-2x) . (-2) + 5.x + 5.(-2)\)

\(= x^3 – 2x^2 – 2x^2 + 4x + 5x – 10\)

\(= x^3 – 4x^2 + 9x – 10\)

b) \((x^2 – 2x + 5) . (2 – x)\)

\(= -x^3 + 4x^2 - 9x + 10\)

* Cách làm: Do 2 – x = - (x – 2)

=> Chúng ngược dấu nhau nên ta chỉ cần đổi dấu các hạng tử.

Bài 7.27 trang 38 SGK Toán 7 tập 2 KNTT

Giả sử ba kích thước của một hình hộp chữ nhật là x; x + 1; x - 1 (cm) với x > 1. Tìm đa thức biểu thị thể tích (đơn vị: \(cm^3\)) của hình hộp chữ nhật đó.

Hướng dẫn giải:

Đa thức biểu thị thể tích của hình hộp chữ nhật:

\(V = x . (x + 1) . (x – 1)\)

\(= x . (x^2 – 1)\)

\(= x^3 – x\)

Bài 7.28 trang 38 SGK Toán 7 tập 2 KNTT

Thực hiện các phép nhân hai đa thức sau:

a) \(5x^3 – 2x^2 + 4x – 4\) và \(x^3 + 3x^2 – 5\);

b) \(-2,5x^4 + 0,5x^2 + 1\) và \(4x^3 – 2x + 6\)

Hướng dẫn giải:

a) \((5x^3 – 2x^2 + 4x – 4)(x^3 + 3x^2 – 5)\)

\(= 5x^3 . x^3 + 5x^3 . 3x^2 + 5x^3 . (-5) + (– 2x^2) . x^3 + (– 2x^2) . (– 2x^2) + (– 2x^2). (-5)\)

\(+ 4x . x^3+ 4x . 3x^2+ 4x . (-5) + (-4) . x^3 + (-4) . 3x^2 + (-4).(-5)\)

\(= 5x^6 + 15x^5 – 25x^3 – 2x^5 + 4x^4 + 10x^2 + 4x^4 + 12x^3 – 20x - 4x^3 – 12x^2 + 20\)

\(= 5x^6 + 13x^5 – 2x^4 – 17x^3 – 2x^2 – 20x + 20\)

b) \((-2,5x^4 + 0,5x^2 + 1)\) và \((4x^3 – 2x + 6)\)

\(= (-2,5x^4) . 4x^3 + (-2,5x^4) . (-2x) + (-2,5x^4) . 6 + 0,5x^2 . 4x^3 + 0,5x^2 . (-2x)\)

\(+ 0,5x^2 . 6 + 4x^3 – 2x + 6\)

\(= -10x^7 + 5x^5 – 15x^4 + 2x^5 - x^3 + 3x^2 + 4x^3 – 2x + 6\)

\(= -10x^7 + 7x^5 – 15x^4 + 3x^3 + 3x^2 – 2x + 6\)

Bài 7.29 trang 38 SGK Toán 7 tập 2 KNTT

Người ta dùng những chiếc cọc để rào một mảnh vườn hình chữ nhật sao cho mỗi góc vườn đều có một chiếc cọc và hai cọc liên tiếp cắm cách nhau 0,1 m. Biết rằng số cọc dùng để rào hết chiều dài của vườn nhiều hơn số cọc dùng để rào hết chiều rộng là 20 chiếc. Gọi số cọc dùng để rào hết chiều rộng là x. Tìm đa thức biểu thị diện tích của mảnh vườn đó.

Hướng dẫn giải:

Theo đề bài:

• Chiều rộng của mảnh vườn là 0,1x (m)
• Chiều dài là 0,1x + 20.0,1 = 0,1x + 2

=> Đa thức biểu thị diện tích của mảnh vườn đó:

\(V = 0,1x + (0,1x + 2) = 0,01x^2 + 0,2x\)