Toán 7 Bài 1: Tổng các góc của một tam giác

Giải Toán 7 Cánh diều tập 2

Giải Toán 7 Cánh diều Bài 1: Tổng các góc của một tam giác sách Cánh diều bao gồm lời giải và đáp án chi tiết cho từng bài tập trong SGK Toán 7 tập 2 chương trình sách mới. Lời giải Toán 7 được trình bày chi tiết, dễ hiểu, giúp các em học sinh ôn tập, củng cố kiến thức được học, từ đó luyện giải Toán 7 hiệu quả. Sau đây mời các bạn tham khảo chi tiết.

Bài 1 trang 72 Toán lớp 7 Tập 2

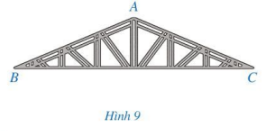
Một khung thép có dạng hình tam giác ABC với số đo các góc ở đỉnh B và đỉnh C cùng bằng 23° (Hình 9). Tính số đo của góc ở đỉnh A.

Hướng dẫn giải:

Ta có: $\widehat A + 23^\circ + 23^\circ = 180^\circ$ $\widehat A + 23^\circ + 23^\circ = 180^\circ$

Suy ra: $\widehat A = 180^\circ - 23^\circ - 23^\circ = 134^\circ$ $\widehat A = 180^\circ - 23^\circ - 23^\circ = 134^\circ$

Bài 2 trang 73 Toán lớp 7 Tập 2

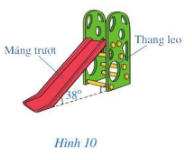
Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo. Tính độ nghiêng của máng trượt so với phương thẳng đứng, biết rằng độ nghiêng của máng trượt so với mặt đất là 38°.

Hướng dẫn giải:

Chiếc cầu trượt được minh họa và đặt tên các đỉnh như hình dưới đây:

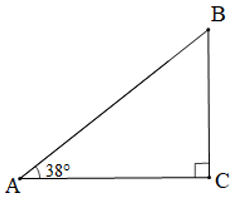
Hình 10 biểu diễn một chiếc cầu trượt gồm máng trượt và thang leo

Tam giác ABC vuông tại C

$\Rightarrow \widehat{A} + \widehat{B} = 90^o$ $\Rightarrow \widehat{A} + \widehat{B} = 90^o$ (trong tam giác vuông, tổng hai góc nhọn bằng 90 ° ).

$\Rightarrow\widehat{B}=90^o-\widehat{A}=90^o-38^o=52^o$ $\Rightarrow\widehat{B}=90^o-\widehat{A}=90^o-38^o=52^o$

Vậy độ nghiêng của máng trượt so với phương thẳng đứng là 52⁰.

Bài 3 trang 73 Toán lớp 7 Tập 2

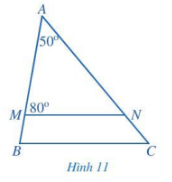
Trong Hình 11, MN // BC. Tính số đo góc C.

Hướng dẫn giải:

Vì MN // BC nên $\widehat{ANM}=\widehat{C}$ $\widehat{ANM}=\widehat{C}$ (2 góc đồng vị)

Áp dụng định lí tổng ba góc trong tam giác AMN có:

$\widehat{A}+\widehat{M} + \widehat{ANM}=180^0$ $\widehat{A}+\widehat{M} + \widehat{ANM}=180^0$

$\Rightarrow \widehat{ANM}= 180^\circ - 50^\circ - 80^\circ = 50^\circ$ $\Rightarrow \widehat{ANM}= 180^\circ - 50^\circ - 80^\circ = 50^\circ$.

Vậy $\widehat{C}=50^0$ $\widehat{C}=50^0$

Bài 4 trang 73 Toán lớp 7 Tập 2

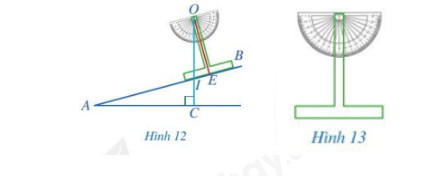
Hình 12 biểu diễn mặt cắt đứng của một đường lên dốc AB. Để đo độ dốc của con đường biểu diễn bởi góc nhọn BAC tạo bới đường thẳng AB và phương nằm ngang AC, người ta làm như sau:

- Làm một thước chữ T như Hình 13;

- Đặt thước chữ T dọc theo cạnh AB như Hình 12, OE \bot AB;

- Buộc một sợi dây vào chân O của thước chữ T và buộc một vật nặng vào đầu dây còn lại, sau đó thả vật nặng để sợi dây có phương thẳng đứng (trong xây dựng gọi là thả dây dọi);

- Tính góc BAC, biết rằng dây dọi OI tạo với trục OE của thước chữ T một góc 15°.

Hướng dẫn giải:

Ta có, trong tam giác OIE: $\widehat I + 15^\circ + 90^\circ = 180^\circ$ $\widehat I + 15^\circ + 90^\circ = 180^\circ$.

Suy ra: $\widehat {OIE} = \widehat {AIC} = 180^\circ - 90^\circ - 15^\circ = 75^\circ$ $\widehat {OIE} = \widehat {AIC} = 180^\circ - 90^\circ - 15^\circ = 75^\circ$.

Vậy góc BAC bằng: $90^\circ - 75^\circ = 15^\circ$ $90^\circ - 75^\circ = 15^\circ$.

....................

Trên đây VnDoc đã gửi tới các bạn tài liệu Giải Toán 7 Bài 1: Tổng các góc của một tam giác. Hy vọng đây là tài liệu hữu ích giúp các em nắm vững kiến thức được học, đồng thời luyện giải Toán 7 hiệu quả.

Bài tiếp theo: Giải Toán 7 Bài 4: Phép nhân đa thức một biến