Toán 7 Bài 2: Tia phân giác của một góc

Giải bài tập Toán 7 tập 1 trang 98, 99 Cánh diều

Tia phân giác của một góc là phần nội dung thuộc chương 4 Toán lớp 7 tập 1 sách Cánh diều. Để giúp các em học sinh nắm vững phần này, VnDoc gửi tới các bạn Giải Toán 7 Cánh diều Bài 2: Tia phân giác của một góc bao gồm đáp án cho các bài tập trong SGK Toán 7 tập 1 trang 98, 99 sách Cánh diều. Lời giải Toán 7 được trình bày chi tiết, dễ hiểu, giúp các em học tốt Toán 7 hơn. Sau đây mời các bạn tham khảo chi tiết.

Bài 1 trang 98 Toán 7 tập 1 CD

Để xác định phương hướng trên bản đồ hay trên thực địa, người ta thường xác định 8 hướng (Bắc, Nam, Đông, Tây, Đông Bắc, Đông Nam, Tây Nam, Tây Bắc) như Hình 29. Trong đó:

B: hướng Bắc;       N: hướng Nam; Đ: hướng Đông;        T: hướng Tây; ĐB: hướng Đông Bắc (tia Ox); ĐN: hướng Đông Nam (tia Ov); TN: hướng Tây Nam (tia Oy); TB: hướng Tây Bắc (tia Ou).

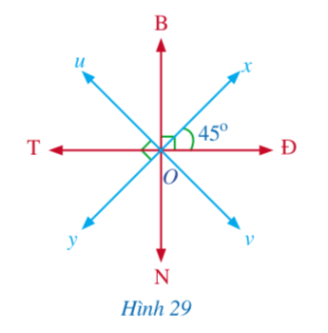a) Tia OB là tia phân giác của những góc nào?

b) Tia OT là tia phân giác của những góc nào?

Hướng dẫn giải:

a) Tia OB là tia phân giác của:

• Góc xOu
• Góc TOĐ

b) Tia OT là tia phân giác của:

• Góc yOu
• Góc BON

Bài 2 trang 99 Toán 7 tập 1 CD

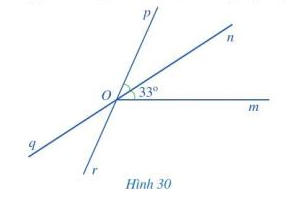
Trong Hình 30, tính số đo của $\widehat{mOp};\widehat{qOr};\widehat{pOq}$

Hướng dẫn giải:

Vì On là tia phân giác của $\widehat{mOp}$ nên $\widehat{mOp}=2.\widehat{mOn}={2.33}^{\circ }={66}^{\circ }$

Vì $\widehat{qOr}=\widehat{mOn}$ ( 2 góc đối đỉnh), mà $\widehat{mOn}={33}^{\circ }\Rightarrow \widehat{qOr}={33}^{\circ }$

Vì $\widehat{pOq}+\widehat{qOr}={180}^{\circ }$( 2 góc kề bù) nên $\widehat{pOq}+{33}^{\circ }={180}^{\circ }\Rightarrow \widehat{pOq}={180}^{\circ }-{33}^{\circ }={147}^{\circ }$

Vậy $\widehat{mOp}={66}^{\circ };\widehat{qOr}={33}^{\circ };\widehat{pOq}={147}^{\circ }$

Bài 3 trang 99 Toán 7 tập 1 CD

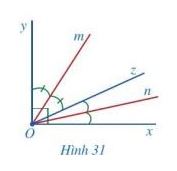
Ở Hình 31 có góc vuông xOy, các tia On, Oz, Om nằm trong góc đó và $\widehat{xOn}=\widehat{nOz},\widehat{yOm}=\widehat{mOz}.$

a) Các tia Om, On có tương ứng là tia phân giác của góc yOz và xOz hay không?

b) Cho biết số đo góc mOn.

Hướng dẫn giải:

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:

Tia Om nằm trong góc yOz và $\widehat{yOm}=\widehat{mOz}$

Tia On nằm trong góc xOz và $\widehat{xOn}=\widehat{nOz}$

b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: $\widehat{yOm}=\widehat{mOz}=\frac{1}{2}.\widehat{yOz};\widehat{xOn}=\widehat{nOz}=\frac{1}{2}.\widehat{xOz}$

Mà tia Oz nằm trong góc xOy nên $\widehat{yOz}+\widehat{xOz}=\widehat{xOy}$

$\Rightarrow \widehat{mOz}+\widehat{zOn}=\frac{1}{2}.\widehat{yOz}+\frac{1}{2}.\widehat{xOz}=\frac{1}{2}.\widehat{xOy}$

Mà tia Oz nằm trong góc mOn nên $\widehat{mOz}+\widehat{zOn}=\widehat{mOn}$ và $\widehat{xOy}={90}^{\circ }\Rightarrow \widehat{mOn}=\frac{1}{2}{.90}^{\circ }={45}^{\circ }$

Bài 4 trang 99 Toán 7 tập 1 CD

Cho $\widehat{xOy}={120}^{\circ }$. Vẽ tia phân giác của góc xOy bằng 2 cách:

a) Sử dụng thước thẳng và compa;

b) Sử dụng thước hai lề

Hướng dẫn giải:

Vẽ góc $\widehat{xOy}={120}^{\circ }$

a) Sử dụng thước thẳng và compa

• Bước 1: Trên tia Ox, lấy điểm A bất kì ( A khác O); vẽ một phần đường tròn tâm O, bán kính OA, cắt tia Oy tại điểm B.
• Bước 2: Vẽ một phần đường tròn tâm A bán kính AO.
• Bước 3: Vẽ một phần đường tròn tâm B bán kính BO, cắt phần đường tròn tâm A bán kính AO tại điểm C nằm trong góc xOy.
• Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.

b) Sử dụng thước hai lề

• Bước 1: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Ox, dùng bút vạch một vạch thẳng theo cạnh của thước.
• Bước 2: Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh Oy, dùng bút vạch một vạch thẳng theo cạnh của thước.
• Bước 3: Hai nét vạch thẳng vẽ ở bước 1 và bước 2 cắt nhau tại điểm C nằm trong góc xOy.
• Bước 4: Vẽ tia OC, ta được OC là tia phân giác của góc xOy.

................