Đề ôn tập hè lớp 7 lên lớp 8 môn Toán năm 2025 - Đề số 1

Đề ôn tập hè lớp 7 lên lớp 8 - Đề số 1 được VnDoc biên soạn bao gồm bài tập ôn hè môn Toán dành cho các em học sinh lớp 7 luyện tập, cùng cố lại kiến thức Toán 7. Đề có đáp án đi kèm cho các em so sánh đối chiếu sau khi làm xong.

Bản quyền thuộc về VnDoc.
Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.

A. Đề ôn tập hè lớp 7 lên lớp 8 môn Toán – Đề số 1

Bài 1: Thực hiện phép tính (tính nhanh nếu có thể)

a, \(0,25 - 3\frac{1}{3} + \frac{{17}}{{12}}\)	b, \(\frac{{ - 9}}{{34}}.\left( { - 3\frac{1}{9}} \right) - \frac{{13}}{{12}}\)
c, \(\left( { - \frac{4}{3} + \frac{7}{{15}}} \right):\frac{6}{5} - \left( {\frac{{ - 1}}{3} + \frac{8}{{15}}} \right):\frac{6}{5}\)	d, \(\left( {\frac{4}{{13}} - \frac{{13}}{4}} \right) - \left[ {\frac{1}{2} - \left( {\frac{9}{{13}} - \frac{1}{8}} \right)} \right]\)

Bài 2: Tìm x, biết:

a, \(\frac{{ - 3}}{4}x = \frac{7}{{16}}\)	b, \(x:\left( { - 3\frac{6}{7}} \right) = - \frac{9}{{21}}\)
c, \(\left( {\frac{{3x}}{7} - 1} \right):\left( { - 2} \right) = \frac{4}{5}\)	d, \(\frac{{ - 13}}{{27}}x + \frac{2}{9} = \left| {\frac{1}{9} - \frac{1}{3}} \right|\)

Bài 3: Tìm ba số x, y, z biết rằng \(\frac{x}{3} = \frac{y}{7};\frac{y}{2} = \frac{z}{5}\) và 7x + 12y – 2z = 140

Bài 4: Cho tam giác ABC có AB = AC, đường phân giác AD

a, Chứng minh AD vuông góc với BC

b, Lấy điểm E thuộc cạnh AB, điểm F thuộc cạnh AC sao cho BE = CF. Chứng minh rằng DA là tia phân giác của góc EDF

Bài 5: Tìm giá trị nhỏ nhất của A, biết: \(A = \left| {7x - 5y} \right| + \left| {2z - 3x} \right| + \left| {xy + yz + zx - 4500} \right|\)

Bài 6: Một khúc gỗ có kích thước như Hình vẽ.

a) Tính thể tích của miếng gỗ.

b) Miếng gỗ này dùng để sẻ thành các miếng nhỏ hơn để làm thước kẻ học sinh có chiều dài 20 cm, chiều rộng là 3 cm và độ dày là 5 mm. Hỏi miếng gỗ này có thể làm thành bao nhiêu chiếc thước nhỏ cho học sinh?

B. Đáp án Đề ôn tập hè lớp 7 lên lớp 8 môn Toán

Bài 1:

a, \(\frac{{ - 5}}{3}\)

b, \(\frac{{ - 53}}{{204}}\)

c, \(\frac{{ - 8}}{9}\)

d, \(\frac{{ - 23}}{8}\)

Bài 2:

a, \(x = \frac{{ - 7}}{{12}}\)

b, \(x = \frac{{81}}{{49}}\)

c, \(x = \frac{7}{5}\)

d, x = 0

Bài 3:

Có \(\frac{x}{3} = \frac{y}{7} \Rightarrow 7x = 3y\) và \(\frac{y}{2} = \frac{z}{5} \Rightarrow 5y = 2z\) thay vào 7x + 12y – 2z = 140 ta có:

3y + 12y – 5y = 140 hay 10y = 140. Suy ra y = 14

Với y = 14 thì x = 6 và z = 35

Vậy x = 6, y = 14, z = 35

Bài 4:

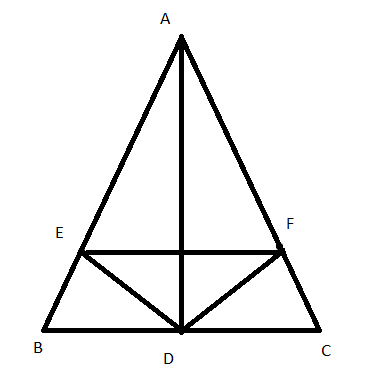
a, + Xét tam giác ABC có AB = AC nên tam giác ABC là tam giác cân

lại có AD là phân giác của góc \(\widehat {BAC}\)

Suy ra AD đồng thời là đường cao, đường trung tuyến của tam giác ABC (tính chất)

Suy ra AD vuông góc với BC

b, + Có AB = AC lại có BE = CF và AB = AE + EB, AC = AF + FC nên AE = AF

+ Xét tam giác AED và tam giác AFD có:

AE = AF (chứng minh trên)

\(\widehat {DAE} = \widehat {DAF}\)(AD là phân giác của góc \(\widehat {BAC}\))

AD chung

Suy ra tam giác AED bằng tam giác AFD theo trường hợp cạnh – góc – cạnh

Suy ra \(\widehat {EDA} = \widehat {FDA}\)(góc tương ứng bằng nhau) hay DA là phân giác của \(\widehat {EDF}\)

Bài 5:

Ta có \(\left| {7x - 5y} \right| \ge 0;\left| {2z - 3x} \right| \ge 0\) và \(\left| {xy + yz + zx - 4500} \right| \ge 0\)

Nên ta có \(A = \left| {7x - 5y} \right| + \left| {2z - 3x} \right| + \left| {xy + yz + zx - 4500} \right| \ge 0\)

Dấu “=” xảy ra khi vào chỉ khi \(\left| {7x - 5y} \right| = \left| {2z - 3x} \right| = \left| {xy + yz + zx - 4500} \right| = 0\)

Với  \(\left| {7x - 5y} \right| = 0 \Leftrightarrow 7x = 5y \Leftrightarrow y = \frac{{7x}}{5}\)

Với \(\left| {2z - 3x} \right| = 0 \Leftrightarrow 2z = 3x \Leftrightarrow z = \frac{{3x}}{2}\)

Với \(\left| {xy + yz + zx - 4500} \right| = 0 \Leftrightarrow xy + yz + zx = 4500\)

\(\Leftrightarrow x.\frac{{7x}}{5} + \frac{{7x}}{5}.\frac{{3x}}{2} + x.\frac{{3x}}{2} = 4500\)

\(\Leftrightarrow 5{x^2} = 4500 \Leftrightarrow {x^2} = 900 \Leftrightarrow \left[ \begin{array}{l} x = 30\\ x = - 30 \end{array} \right.\)

Với x = 30 thì y = 42, z = 45

Với x = -30 thì y = -42, z = -45

Bài 6: Một khúc gỗ có kích thước như Hình vẽ.

a) Tính thể tích của miếng gỗ.

b) Miếng gỗ này dùng để sẻ thành các miếng nhỏ hơn để làm thước kẻ học sinh có chiều dài 20 cm, chiều rộng là 3 cm và độ dày là 5 mm. Hỏi miếng gỗ này có thể làm thành bao nhiêu chiếc thước nhỏ cho học sinh?

Lời giải:

a) Thể tích của miếng gỗ là:

20 . 6 . 3 = 360 (cm³)

5 mm = 0,5 cm

Thể tích một chiếc thước kẻ là:

20 . 3 . 0,5 = 30 (cm³)

Có thể làm số chiếc thước kẻ là:

360 : 30 = 12 (chiếc)

Đáp số: 12 chiếc.