Các trường hợp bằng nhau của tam giác
Chứng minh hai tam giác bằng nhau
Các trường hợp bằng nhau của tam giác bao gồm trường hợp cạnh - cạnh - canh, cạnh - góc - cạnh, góc - cạnh - góc. Đây là nội dung quan trọng được học trong chương trình Toán 7 học kỳ 1. Dưới đây VnDoc sẽ gửi tới các bạn lý thuyết 3 trường hợp bằng nhau của tam giác, kèm các dạng Toán thương gặp như Chứng minh hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau... Ngoài ra còn có bài tập vận dụng cho các em luyện tập. Sau đây mời các em tham khảo chi tiết.
1. Các trường hợp bằng nhau của tam giác
a) Trường hợp 1: cạnh – cạnh – cạnh:
a) Trường hợp 1: cạnh – cạnh – cạnh: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
b) Trường hợp 2: cạnh – góc – cạnh: Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
c) Trường hợp 3: góc – cạnh – góc: Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
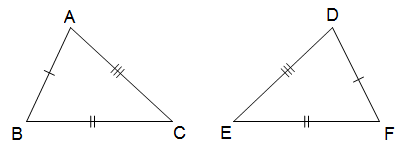
+ Xét ∆ABC và ∆DFE có:
AB = DF (gt)
AC = DE (gt)
BC = EF (gt)
Suy ra ∆ABC = ∆DFE (c - c - c)
\(\Rightarrow \widehat{A} = \widehat{D};\widehat{B} = \widehat{F};\widehat{C} = \widehat{F}\) (các cặp góc tương ứng)
Tham khảo thêm: Trắc nghiệm Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
b) Trường hợp 2: cạnh – góc – cạnh:
Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
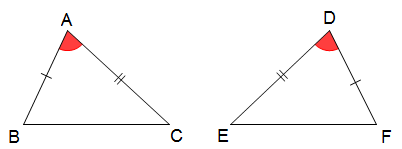
+ Xét ∆ABC và ∆DFE có:
AB = DF (gt)
\(\widehat{A}=\widehat{D}\) (gt)
AC = DE (gt)
Suy ra ∆ABC = ∆DFE (c - g - c)
\(\Rightarrow\widehat{B}=\widehat{F};\widehat{C}=\widehat{E}\) (góc tương ứng) và BC = EF (cạnh tương ứng)
Lưu ý: Cặp góc bằng nhau phải xen giữa hai cặp cạnh bằng nhau thì mới kết luận được hai tam giác bằng nhau.
Tham khảo thêm: Trắc nghiệm Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
c) Trường hợp 3: góc – cạnh – góc:
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
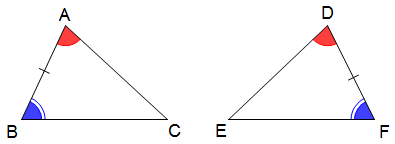
+ Xét ∆ABC và ∆DFE có:
\(\widehat{A}=\widehat{D}\) (gt)
AB = DF (gt)
\(\widehat{B}=\widehat{F}\)
Suy ra ∆ABC = ∆DFE (g - c - g)
\(\Rightarrow\widehat{C}=\widehat{E}\) (góc tương ứng) và AC = DE, BC = EF (cạnh tương ứng)
Lưu ý:
- Cặp cạnh bằng nhau phải là cạnh tạo nên hai cặp góc bằng nhau thì mới kết luận được hai tam giác bằng nhau.
- Khi hai tam giác đã chứng minh bằng nhau, ta có thể suy ra những yếu tố tương ứng còn lại bằng nhau.
Tham khảo thêm: Trắc nghiệm Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
2. Các trường hợp bằng nhau của tam giác vuông
* Trường hợp cạnh góc vuông - cạnh góc vuông (cgv - cgv): Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
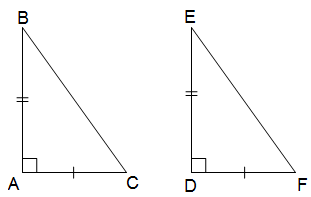
* Trường hợp cạnh góc vuông - góc nhọn (cgv - gn): Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề ấy cạnh của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
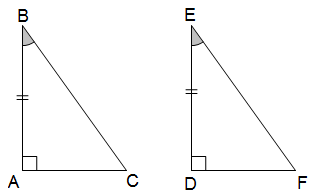
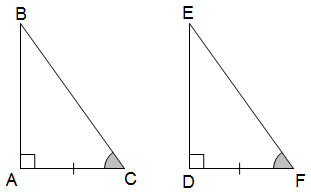
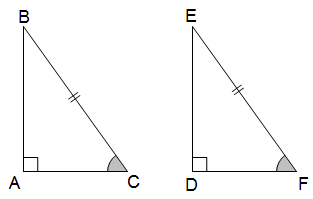
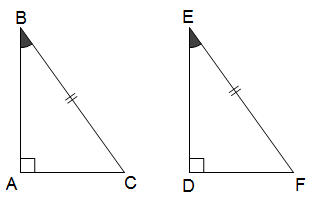
* Trường hợp cạnh huyền - góc nhọn (ch - gn): Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
3. Ứng dụng các trường hợp bằng nhau của tam giác
Chúng ta thường vận dụng các trường hợp bằng nhau của tam giác để:
- Chứng minh: hai tam giác bằng nhau, hai đoạn thẳng bằng nhau, hai góc bằng nhau; hai đường thẳng vuông góc; hai đường thẳng song song; ba điểm thẳng hàng; ...
- Tính: các độ dài đoạn thẳng; tính số đo góc; tính chu vi; diện tích; ...
- So sánh: các độ dài đoạn thẳng; so sánh các góc; ...
4. Bài tập vận dụng Các trường hợp bằng nhau của tam giác
a) Trường hợp 1: cạnh – cạnh – cạnh
Bài 1: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán bính BA, chúng cách nhau giữa ở D (D và B nằm khác phía đối với bờ AC). Chứng minh rằng AD // BC
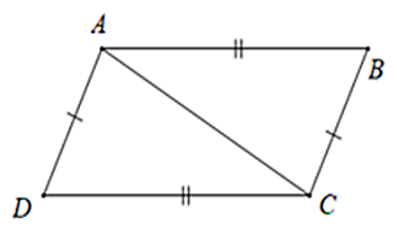
Xét ΔABC và ΔCDA có AC chung
AB = CD (gt)
BC = DA (gt)
Nên ΔABC = ΔCDA (c-c-c)
⇒ \(\widehat{ABC}=\widehat{CAD}\) (hai góc tương ứng bằng nhau)
mà hai góc ở vị trí so le trong
Do đó AD // BC
Bài 2: Tam giác ABC có AB = AC, M là trung điểm của BC. Chứng mình rằng AM vuông góc với BC.
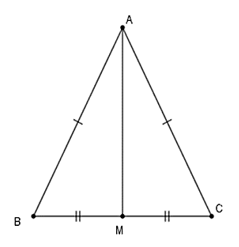
Xét ΔAMB và ΔAMC có:
AB = AC
AM chung
MB = MC (gt)
⇒ ΔAMB = ΔAMC (c-c-c)
Suy ra \(\widehat{BAM}=\widehat{CAM};\widehat{AMB}=\widehat{AMC}\)(góc tương ứng bằng nhau)
Mà \(\widehat{AMB}+\widehat{AMC}={180}^0\)(hai góc kề bù)
Nên \(\widehat{AMB}=\widehat{AMC}=\frac{{180}^0}{2}={90}^0\) hay AM ⊥ BC
b) Trường hợp 2: cạnh – góc – cạnh
Bài 1: Cho đoạn thẳng BC. Gọi A là một điểm nằm trên đường trung trực xy của đoạn thẳng BC và M là giao điểm của xy với BC. Chứng minh AB = AC
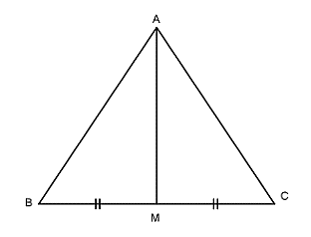
Xét hai tam giác AMB và AMC có:
MB = MC (gt)
\(\widehat{AMB}=\widehat{AMC}={90}^0\) (vì AM ⊥ BC)
AH là cạnh chung
Nên ΔAMB = ΔAMC (c-g-c)
⇒ AB = AC (hai cạnh tương ứng)
Bài 2: Cho đường thẳng AB, trên hai nửa mặt phẳng đối nhau bờ là đoạn thẳng AB vẽ hai tia Ax ⊥ AB; By ⊥ BA. Trên Ax và By lần lượt lấy hai điểm C và D sao cho AC = BD. Gọi O là trung điểm của AB.
a) Chứng mình rằng: ΔAOC = ΔBOD
b) Chứng minh O là trung điểm của CD
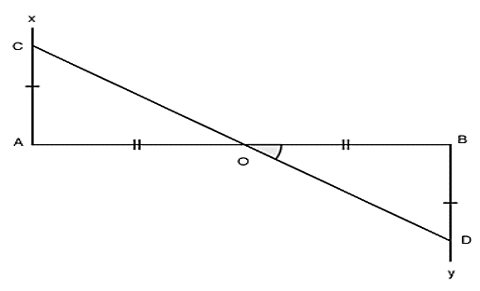
\(\widehat{OAC}=\widehat{OBD}={90}^0\)(gt)\(\Rightarrow\widehat{AOC}=\widehat{BOD};OC = OD\)Mà tia OC và OD là hai tia nằm khác phía đối với AB nên suy ra O, C, D thẳng hàng (hai tia đối của hai góc đối đỉnh hay O nằm giữa CD)
Ta có: O nằm giữa C và D nên OC = OD hay O là trung điểm của CD
c) Trường hợp 3: góc – cạnh – góc:
Bài 1: Cho ΔABC có \(\widehat{B}=\widehat{C}\). Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thằng BD và CE.
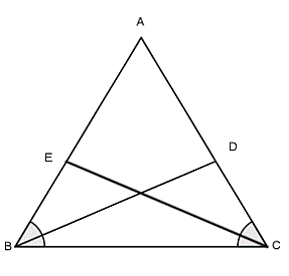
Xét ∆EBC và ∆DCB có:
\(\widehat{EBC}=\widehat{DCB}\) (gt)
BC chung
\(\widehat{ECB}=\widehat{DCB}\)
Suy ra ∆EBC = ∆DCB (g - c - g)
Suy ra BD = CE (cặp cạnh tương ứng bằng nhau)
Bài 2: Cho tam giác ABC (AB = AC) và I là trung điểm của đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm nằm trên tia Cx sao cho BD = CE. Chứng minh rằng ba điểm D, I, E thẳng hàng.
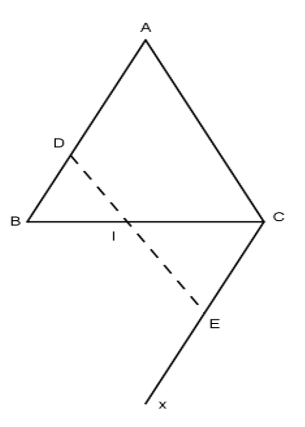
Xét ∆BID và ∆CIE ta có:
BI = IC (I là trung điểm của BC)
\(\widehat{IBD}=\widehat{ICE}\) (hai góc so le trong)
BD = CE (gt)
⇒ ΔBID = ΔCIE (c-g-c)
Nên \(\widehat{BID}=\widehat{CIE}\) (hai góc tương ứng bằng nhau)
Hai góc này bằng nhau, chiếm vị trí đối đỉnh, có hai cạnh tương ứng BI và CI nằm trên một đường thẳng.
Vậy D, I, E thẳng hàng
5. Bài tập trắc nghiệm Hai tam giác bằng nhau
Câu 1: Cho ∆ PQR = ∆ DEF trong đó PQ = 4cm, QR = 6cm, PR = 5cm. Chu vi tam giác DEF là:
| A. 14cm | B. 15cm |
| C. 16cm | D. 17cm |
Câu 2: Cho ΔABC = ΔMNP. Biết AB = 5cm, MP = 7cm và chu vi của tam giác ABC bằng 22cm. Tính các cạnh còn lại của mỗi tam giác?
| A. NP = BC = 9cm | B. NP = BC = 11cm |
| C. NP = BC = 10cm | D. NP = 9cm; BC = 10cm |
Câu 3: Cho DΔABC = ΔMNP có AB = 7cm, AC = 10cm, NP = 12cm. Tính chu vi tam giác MNP:
| A. 27cm | B. 29cm |
| C. 32cm | D. 37cm |
Câu 4: Cho ΔIEF = ΔMNO. Hãy tìm cạnh tương ứng với cạnh EF, góc tương ứng với góc E:
A.MN và góc O
B.MO và góc M
C.NO và góc N
Câu 5: Cho hai tam giác bằng nhau: Tam giác ABC (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) và môt tam giác có ba đỉnh là T, S, R. Hãy viết kí hiệu về sự bằng nhau của hai tam giác đó biết rằng góc A bằng góc T và AC = TS.
| A. ΔABC = ΔTRS | B. ΔABC = ΔRTS |
| C. ΔABC = ΔSTR | D. ΔABC = ΔTSR |
Câu 6: Cho △ABC=△DEF. Biết rằng AB = 5cm; AC = 12cm; EF = 12cm. Tính chu vi tam giác DEF là
A. 30cm
B. 22 cm
C. 18 cm
D. 20 cm
Câu 7: Cho △ABC=△DEF. Biết rằng AB = 6cm; AC = 8cm; EF = 10cm. Tính chu vi tam giác DEF là
A. 24cm
B. 20cm
C. 18 cm
D. 30 cm
Câu 11: Cho △DEF=△MNP. Biết EF+FD=10cm; NP−MP=2cm; DE=3cm. Tính độ dài cạnh FD
A. 4 cm
B. 6 cm
C. 8 cm
D. 10 cm
Đáp án trắc nghiệm Hai tam giác bằng nhau
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 |
| B | C | B | C | A |
| Câu 6 | Câu 7 | Câu 8 | ||
| A | A | A |
6. Bài tập tự luyện
Sau khi nắm rõ các lý thuyết bên trên về những trường hợp bằng nhau của tam giác, mời các bạn cùng làm các bài tập ứng dụng dưới đây:
Bài 1: Cho tam giác ABC; M là trung điểm BC; N là 1 điểm trong tam giác sao cho NB = NC.
Chứng minh: ∆NMB = ∆ NMC.
Bài 2. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng: ABE = ACE
Bài 3. Cho tam giác ABC có góc A = 400, AB = AC. Gọi M là trung điểm của BC. Tính các góc của tam giác AMB và tam giác AMC.
Bài 4. Cho tam giác ABC (AB < AC) có AM là phân giác của góc A (M thuộc BC). Trên AC lấy D sao cho AD = AB.
a. Chứng minh BM = MD
b. Gọi K là giao điểm của AB và DM. Chứng minh ∆DAK = ∆BAC
Bài 5. Cho tam giác ABC vuông ở C, có góc A bằng 600, tia phân giác của góc BAC cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB), kẻ BD vuông góc với AE (D thuộc AE). Chứng minh:
a. AK = KB
b. AD = BC
Bài 6. Cho tam giác ABC. Qua A kẻ đường thẳng song song với BC, qua C kẻ đường thẳng song song với AB. Hai đường thẳng cắt nhau tại D.
a. Chứng minh ∆ABC =∆ADC
b. Chứng minh ∆ADB = ∆CBD
c. Gọi O là giao điểm của AC và BD. Chứng minh ∆ABO = ∆COD
Bài 7. Cho góc xAy khác góc bẹt. Gọi AD là tia tia phân giác của góc xAy. Qua D kẻ đường thẳng vuông góc với Ay cắt Ay tại C và cắt Ax tại E. Qua D kẻ đường thẳng vuông góc với Ax cắt Ax tại B và cắt Ay tại H. Chứng minh:
a. ∆ABD = ∆ACD
b. ∆DBE = ∆DCH
c. ∆ABH = ∆ACE
Bài 8. Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và D. Trên tia Oy lấy hai điểm C và E sao cho OD = OE và OA = OB.
a. Chứng minh ∆ODC = ∆OBE
b. Gọi A là giao điểm của BE và CD. Chứng minh ∆AOB = ∆AOC
c. Chứng minh BC vuông góc với OA
Bài 9. Cho tam giác ABC có AB = AC. D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a. Chứng minh góc EAB = góc DAC.
b. Gọi M là trung điểm của BC. Chứng minh AM là phân giác của góc DAE.
c. Giả sử góc DAE = 600. Tính các góc còn lại của tam giác DAE.
Bài 10. Cho ABC có AB = AC. Kẻ AE là phân giác của góc BAC (E thuộc BC). Chứng minh rằng:
a. ∆ABE = ∆ACE
b. AE là đường trung trực của đoạn thẳng BC.
Bài 11. Cho ABC có AB < AC. Kẻ tia phân giác AD của góc BAC (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:
a. ∆BDF = ∆EDC.
b. BF = EC.
c. F, D, E thẳng hàng.
d. AD ⊥ FC
Bài 12. Cho góc nhọn xOy. Trên tia Ox, lấy 2 điểm A và C. Trên tia Oy lấy 2 điểm B và D sao cho OA = OB; OC = OD. (A nằm giữa O và C; B nằm giữa O và D).
a. Chứng minh ∆OAD = ∆OBC
b. So sánh 2 góc CAD và CBD.
Bài 13. Cho ΔABC vuông ở A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
a. Chứng minh ΔABC = ΔABD
b. Trên tia đối của tia AB, lấy điểm M. Chứng minh ΔMBD = ΔMBC.
Bài 14. Cho góc nhọn xOy và tia phân giác Oz của góc đó. Trên Ox, lấy điểm A, trên Oy lấy điểm B sao cho OA = OB. Trên tia Oz, lấy điểm I bất kì. Chứng minh:
a. ΔAOI = ΔBOI.
b. AB ⊥ OI.
Bài 15. Cho ΔABC, M là trung điểm của BC. Trên tia đối của tia MA, lấy điểm E sao cho ME = MA.
a. Chứng minh AC // BE.
b. Gọi I là một điểm trên AC, K là một điểm trên EB sao cho AI = EK. Chứng minh 3 điểm I, M, K thẳng hàng.
Bài 16: Chứng minh hai tam giác bằng nhau thì hai đường cao tương ứng bằng nhau.
Bài 17: Cho góc vuông xAy. Trên tia Ax lấy 2 điểm B và D, trên tia Ay lấy 2 điểm C và E sao cho AB = AC và AD = AE
a. Chứng minh tam giác ACD và tam giác ABE bằng nhau.
b. Chứng minh tam giác BOD và tam giác COE bằng nhau. Với O là giao điểm của DC và BE.
c. Chứng minh AO vuông góc với DE.
Bài 18: Cho góc xOy khác góc bẹt, trên tia Ox lấy 2 điểm A và D trên tia OY lấy 2 điểm C và E sao cho OD = OE và OA = OB
a. Chứng minh tam giác ODC và tam giác OBE bằng nhau.
b. Gọi A là giao điểm của BE và CD. Chứng minh tam giác AOB và tam giác AOC bằng nhau.
c. Chứng minh BC vuông góc với OA.
Bài 19: Cho tam giác ABC có AB = AC. Tia phân giác của góc A cắt BC tại M.
a) Chứng minh: ∆AMB = ∆AMC.
b) Chứng minh M là trung điểm của cạnh BC.
c) K là một điểm bất kì trên đoạn thẳng AM, đường thẳng CK cắt cạnh AB tại I. Vẽ IH vuông góc với BC tại H. Chứng minh góc BAC bằng hai lần góc BIH.
-----------------------------------------------------
Ngoài tài liệu Các trường hợp bằng nhau của tam giác, mời các bạn tham khảo thêm các tài liệu học tập lớp 7, Đề thi giữa kì 2 lớp 7, Đề thi học kì 2 lớp 7... cũng được cập nhật liên tục trên VnDoc.com.
