Giải bài tập SBT Toán 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

Giải bài tập SBT Toán 7 bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

Giải bài tập SBT Toán 7 bài 6: Tam giác cân

Câu 1: Vẽ tam giác ABC biết ∠B =90^o,∠C =60^o, BC = 2cm. Sau đó đo AC để kiểm tra rằng AC = 4cm.

Lời giải:

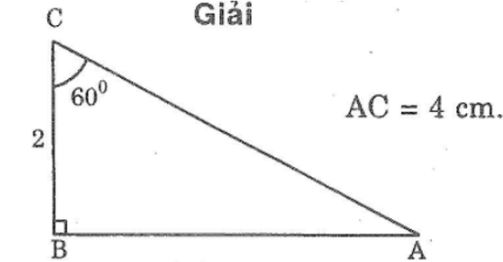
Câu 2: Tìm các tam giác bằng nhau ở hình dưới (không xét tam giác mà các cạnh chưa được kẻ)

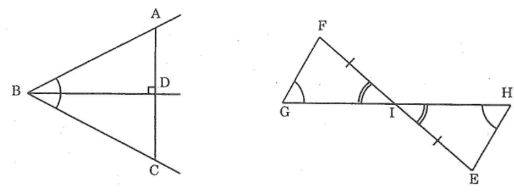
Lời giải:

Ta có: ΔABD= ΔCBD (g.c.g)

ΔGIF= ΔHIE (g.c.g)

Câu 3: Cho tam giác ADE có ∠AD=∠AE . Tia phân giác của góc D cắt AE ở điểm M. tia phân giác của góc E cắt AD ở điểm N. So sánh các độ dịa DN và EM

Lời giải:

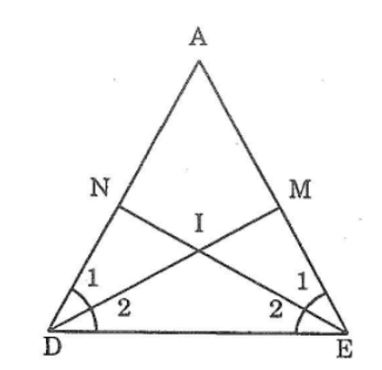
Tam giác ADE có: ∠D =∠E (gt)

∠(D1) =∠(D2) = (1/2)∠D (vì DM là tai phân giác)

∠(E1) = ∠(E2) = (1/2)∠E (vì EN là tia phân giác)

Suy ra: ∠(D1) =∠(D2) =∠(E1) =∠(E2)

xét ΔDNE và ΔEMD, ta có:

∠(NDE) =∠(MED) (gt)

DE cạnh chung

∠(D2) =∠(E2) (chứng minh trên)

Suy ra: ΔDNE= ΔEMD (g.c.g)

Vậy DE = EM (hai góc tương ứng)

Câu 4: Cho hình bên, trong dod AB // HK, AH // BK.Chứng minh rằng AB = HK; AH = BK

Lời giải:

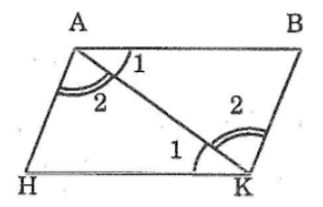
Nối AK, ta có:

AB // HK (gt)

⇒ ∠(A1) =∠(K1) (hai góc so le trong)

AH // BK (gt)

⇒ ∠ (A2) =-∠(K2) (hai góc so le trong)

Xét ΔABK và ΔKHA, ta có:

∠(A1) =∠(K1)

AK canh chung

∠(A2) =∠(K2)

Suy ra: ΔABK =ΔKHA (g.c.g)

Vậy: AB = KH; BK = AH ( 2 cạnh tương ứng)

Câu 5: Cho tam giác ABC. Các tua phân giác của các góc B và C cắt nhau ở O. Kẻ OD⊥AC, kẻ OE⊥AB. Chứng minh rằng OD = OE

Lời giải:

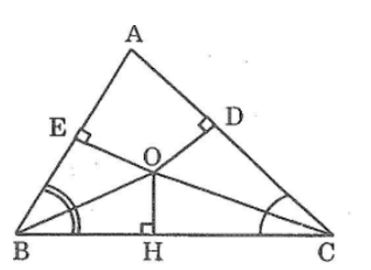
Kẻ OH⊥BC

Xét hai tam giác vuông OEB và OHB, ta có:

∠(OEB) =∠OHB=90^o

Cạnh huyền OB chung

∠(EBO) =∠(HBO)

Suy ra Δ OEB = Δ OHB (cạnh huyền góc nhọn)

⇒OE = OH (hai cạnh tương ứng)

Xét hai tam giác vuông OHC và ODC, ta có:

∠(OHC) =∠ODC=90^o

Cạnh huyền OB chung

∠(HCO) =∠(DCO)

Suy ra Δ OHC = Δ ODC (cạnh huyền góc nhọn)

⇒OD = OH (hai cạnh tương ứng)

Từ (1) và (2) suy ra: OE = OD

Câu 6: Cho tam giác ABC có AB = AC. Lấy điểm D trân cạnh AB, điểm E trên cạnh AC sao cho AD = AE

a, Chứng minh rằng BE = CD

b, Gọi O là giao điểm của BE và CD

Chứng minh rằng ΔBOD=COE

Lời giải:

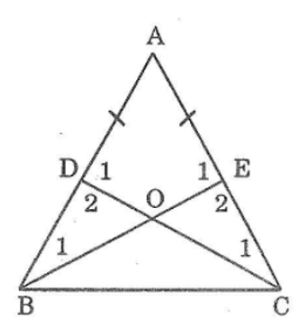
a, Xét ΔBEA và CDA, ta có:

BA = CA (gt)

∠A chung

AE=AD

Suy ra: ΔBEA= CDA (c.g.c)

Vậy: BE = CD (hai cạnh tương ứng)

b, ΔBEA= ΔCDA (chứng minh trên)

⇒∠(B1) =∠(C1);∠(E1) =∠(D1) (hai góc tương ứng)

∠(E1) +∠(E2) =180^o (hai góc kề bù)

∠(D1) +∠(D2) =180^o (hai góc kề bù)

Suy ra: ∠(E2) =∠(D2)

AB = AC (gt)

⇒AE + EC = AD = BD MÀ AE = AD (GT)⇒EC = BD

Xét ΔODB và ΔOCE, ta có:

∠(E2) =∠(D2) (chứng minh trên)

DB=EC (chứng minh trên)

∠(B1) =∠(C1)

Suy ra: ΔODB= ΔOCE

Câu 7: Cho tam giác ABC có ∠B =∠C Tia phân giác của góc A cắt BC tại D chứng minh rằng: BD = DC; AB = AC

Lời giải:

Trong ΔADB, ta có:

∠B +∠(A1) +∠(D1) =180^o (tổng 3 góc trong tam giác)

Suy ra: ∠(D1) =180^o-(∠C +(A1)) (1)

Trong ΔADC, ta có:

∠C +∠(A2) +∠(D2) =180^o (tổng 3 góc trong tam giác)

Suy ra: ∠(D2) =180^o-(∠C +∠(A2)) (2)

∠B =∠C (gt)

∠(A1) =∠(A2) (gt)

Từ (1) và (2) và gt suy ra: ∠(D1) =∠(D2)

Xét ΔABD và ΔADC, ta có:

∠(A1) =∠(A2)(gt)

AD cạnh chung

∠(D1) =∠(D2)

Vậy: ΔABD= ΔADC (g.c.g)

Vậy: AB = AC (hai cạnh tương ứng)

DB = DC (hai cạnh tương ứng)

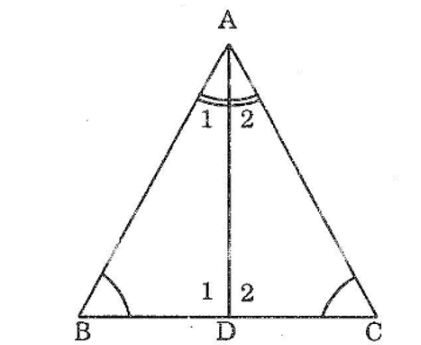
Câu 8: Cho hình dưới, chứng minh rằng O là trung điểm của mỗi đoạn thẳng AD, BC

Lời giải:

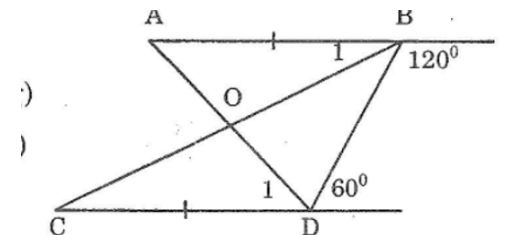
Hai đường thẳng AB và CD tạo với BD có hai góc trong cùng phía bù nhau: 120^o+60^o=180^o

Suy ra: AB // CD

Ta có: ∠A =∠(D1) (hai góc so le trong)

∠C =∠(B1) (hai góc so le trong)

AB = CD (gt)

Suy ra: Δ AOB= Δ DOC (g.c.g)

Suy ra: OA = OD; OB = OC (hai cạnh tương ứng)

Vậy O là trung điểm của mỗi đoạn thẳng AD và BC