Giải bài tập SBT Toán 7 bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 8: Các trường hợp bằng nhau của tam giác vuông

Giải bài tập SBT Toán 7 bài: Ôn tập chương II

Giải bài tập SBT Toán 7 bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Câu 1: So sánh các góc của tam giác ABC biết rằng AB = 5cm, BC = 5cm, AC = 3cm.

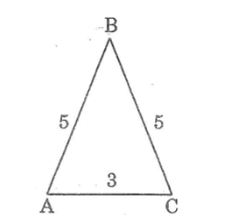
Lời giải:

Ta có: AB = BC nên ΔABC cân tại B

Suy ra: ∠A = ∠C

Vì BC > AC nên ∠A > ∠B (đối diện cạnh lớn hơn là góc lớn hơn)

Vậy ∠A = ∠C > ∠B.

Câu 2: So sánh các cạnh của tam giác ABC biết rằng ∠A = 80^o, ∠C = 40^o

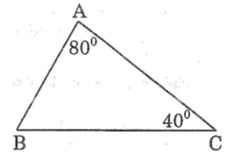
Lời giải:

Ta có: ∠A + ∠B + ∠C = 180^o (tổng ba góc trong tam giác)

Suy ra: ∠B = 180^o - (∠A + ∠C )

= 180^o - (80^o + 40^o) = 60^o

Trong ΔABC, ta có: ∠A > ∠B > ∠C

Suy ra: BC > AC > AB (đối diện với góc lớn hơn là cạnh lớn hơn).

Câu 3: Cho tam giác ABC có B > 90^o, điểm D nằm giữa B và C. Chứng minh rằng AB < AD < AC

Lời giải:

Trong ∆ABD ta có: ∠B > 90^o

⇒ ∠B > ∠D1 ⇒ AD > AB (đối diện góc lớn hơn là cạnh lớn hơn) (1)

Trong ΔABD ta có: ∠D2 là góc ngoài tại đỉnh D nên ∠D2 > ∠B > 90^o

Trong ΔADC ta có: ∠D2 > 90^o

⇒ ∠D2 > ∠C ⇒ AC > AD (cạnh đối diện góc lớn hơn là cạnh lớn hơn) (2)

Từ (1) và (2) suy ra: AB < AD < AC

Câu 4: Hãy lựa chọn đúng sai với các câu dưới đây

1. Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất
2. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất
3. Trong một tam giác, đối diện cạnh nhỏ nhất là góc nhọn
4. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù

Lời giải:

1. Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất Đ
2. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất Đ
3. Trong một tam giác, đối diện cạnh nhỏ nhất là góc nhọn Đ
4. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù S

Câu 5: Cho tam giác ABC vuông tại A, điểm K nằm giữa A và C. So sánh độ dài BK, BC.

Lời giải:

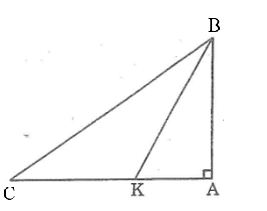
Trong ΔABK, ta có BKC là góc ngoài tại đỉnh K.

Suy ra: ∠BKC > ∠A = 90^o (tính chất góc ngoài)

Trong ΔBKC ta có ∠BKC là góc tù, BC là cạnh đối diện với ∠BKC nên BC > CK.

Câu 6: Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. So sánh các độ dài AD, DC.

Lời giải:

Kẻ DH ⊥ AC.

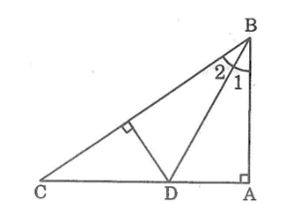
Xét hai tam giác vuông ABD và HBD, ta có:

∠B1 = ∠B2 (gt)

Cạnh huyền BD chung

Suy ra: ΔABD = ΔHBD (cạnh huyền, góc nhọn)

⇒ AD = HD (2 cạnh tương ứng) (1)

Trong tam giác vuông DHC có ∠DHC = 90^o

⇒ DH < DC (cạnh góc vuông nhỏ hơn cạnh huyền) (2)

Từ (1) và (2) suy ra: AD < DC

Câu 7: Cho tam giác ABC có AB < AC. Tia phân giác của góc A cắt BC ở D. So sánh các độ dài BD, DC.

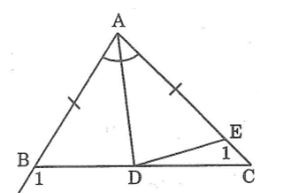
Lời giải:

Trên cạnh AC lấy điểm E sao cho AE = AB.

Ta có: AB < AC nên AE < AC

Suy ra E nằm giữa A và C.

Xét ΔABD và ΔAED, ta có:

AB = AE (theo cách vẽ)

∠(BAD) = ∠(EAD) (gt)

AD cạnh chung

Suy ra: ΔABD = ΔAED (c.g.c)

Suy ra: BD = DE (2 cạnh tương ứng)

và ∠(ABD) = ∠(AED) (2 góc tương ứng)

Mà: ∠(ABD) + ∠B1= 180^o (2 góc kề bù)

∠(AED) + ∠E1= 180^o (2 góc kề bù)

Suy ra: ∠B1= ∠E1

Trong ΔABC ta có ∠B1là góc ngoài tại đỉnh B

Ta có: ∠B1 > ∠C (tính chất góc ngoài của tam giác)

Suy ra: ∠E1> ∠C

Suy ra: DC > DE (đối diện góc lớn hơn là cạnh lớn hơn)

Vậy BD < DC.

Câu 8: Chứng minh rằng nếu một tam giác vuông có một góc nhọn bằng 30o thì cạnh góc vuông đối diện với nó bằng nửa cạnh huyền.

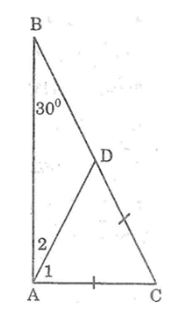
Lời giải:

Xét ΔABC, ta có: ∠A= 90^o; ∠B= 30^o

Trên cạnh BC lấy điểm D sao cho CD = AC

Ta có: ΔACD cân tại C

Mà ∠C + ∠B = 90^o (tính chất tam giác vuông)

Suy ra: ∠C = 90^o - ∠B = 90^o - 30^o = 60^o

Suy ra: ΔACD đều

Suy ra: AC = AD = DC và ∠A1= 60^o

Ta có: ∠A1+ ∠A2 = ∠BAC = 90^o

⇒ ∠A2 = 90^o - ∠A1 = 90^o - 60^o = 30^o

Trong ΔADB, ta có: ∠A2 = ∠B= 30^o

Suy ra: ΔADB cân tại D (vì có 2 góc kề cạnh AB bằng nhau)

Hay AD = DB

Suy ra: AC = CD = DB mà CD + DB = BC

Vậy AC = 1/2 BC.

Câu 9: Chứng minh định lý “Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn” theo gợi ý sau:

Cho tam giác ABC có ∠B > ∠C

a, Có thể xảy ra AC < AB hay không?

b, Có thể xảy ra AC = AB hay không?

Lời giải:

a, Nếu AB > AC thì ∠C > ∠B (góc đối diện với cạnh lớn hơn là góc lớn hơn)

Điều này trái với giả thiết ∠B > ∠C nên không xảy ra.

b, Nếu AB = AC thì ΔABC cân tại A

⇒ ∠B = ∠C(tính chất tam giác cân)

Điều này trái với giả thiết ∠B = ∠C nên không xảy ra.

Vậy ∠B > ∠C hay AC > AB.