Giải bài tập SBT Toán 7 bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu
Bài tập môn Toán lớp 7
Giải bài tập SBT Toán 7 bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.
Giải bài tập SBT Toán 7 bài: Ôn tập chương II
Giải bài tập SBT Toán 7 bài 1: Quan hệ giữa góc và cạnh đối diện trong một tam giác
Giải bài tập SBT Toán 7 bài 3: Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác
Câu 1: Cho hình sau. So sánh các độ dài AB, AC, AD, AE.
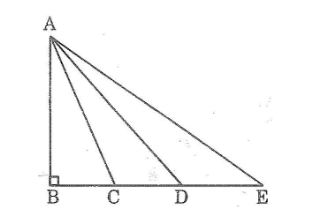
Lời giải:
Vì điểm C nằm giữa B và D nên BC < BD (1)
Vì điểm D nằm giữa B và E nên BD < BE (2)
Từ (1) và (2) suy ra: BC < BD < BE
Vì B, C, D, E thẳng hành và AB ⊥ BE nên:
AB < AC < AD < AE
(đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn)
Câu 2: Cho hình bên. Chứng minh rằng MN < BC.
Lời giải:
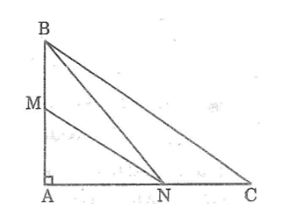
Nối BN.
Vì M nằm giữa A và B nên AM < AB
Ta có: NA ⊥ AB
Suy ra: NM < NB (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn) (1)
Vì N nằm giữa A và C nên AN < AC
Lại có: BA ⊥ AC
Suy ra: BN < BC (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn) (2)
Từ (1) và (2) suy ra: MN < BC
Câu 3: Cho tam giác ABC cân tại A có AB = AC = 10cm, BC = 12cm. Vẽ cung tròn tâm A có bán kính 9cm. Cung đó có cắt đường thẳng BC hay không, có cắt cạnh BC hay không? Vì sao?
Lời giải:
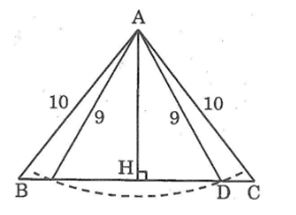
Kẻ AH ⊥ AB.
Xét hai tam giác vuông AHB và AHC, ta có:
∠AHB = ∠AHC = 90o
AB = AC (gt)
AH cạnh chung
Suy ra: ΔAHB = ΔAHC
(cạnh huyền - cạnh góc vuông)
Suy ra: HB = HC (hai cạnh tương ứng)
Ta có: HB = HC = BC2 = 6 (cm)
Trong tam giác vuông AHB có ∠AHB = 90o
Áp dụng định lí Pi-ta-go, ta có:
AB2 = AH2 + HB2 ⇒ AH2 = AB2 - HB2 = 102 - 62 = 64
⇒ AH = 8 (cm)
Do bán kính cung tròn 9(cm) > 8(cm) nên cung tròn tâm A bán kính 9 cm cắt đường thẳng BC.
Gọi D là giao điểm của cung tròn tâm A bán kính 9 cm với BC.
Vì đường xiên AD < AC nên hình chiếu HD < HC.
Do đó D nằm giữa H và C.
Vậy cung tròn tâm A bán kính 9 cm cắt cạnh BC.
Câu 4: Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.
Lời giải:
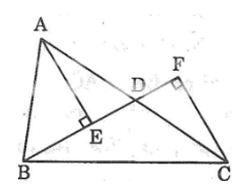
Trong ∆ADE, ta có ∠(AED) = 90o
Suy ra: AE < AD (1)
Trong ∆CFD, ta có ∠(CFD) = 90o
Suy ra: CF < CD(2)
Cộng từng vế (1) và (2), ta có:
AE + DF < AD + CD
Vì D nằm giữa A và C nên AD + CD = AC
Vậy AE + CF < AC.
Câu 5: Cho tam giác ABC vuông tại A, M là trung điểm của AC. Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BM. Chứng minh rằng AB < (BE + BF) / 2.
Lời giải:
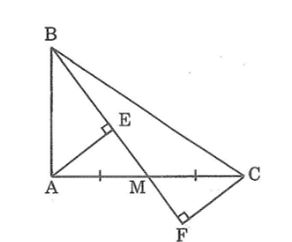
Trong ∆ABM, ta có ∠(BAM) = 90o
Suy ra: AB < BM
Mà BM = BE + EM = BF - MF
Suy ra: AB < BE + EM
AB < BF - FM
Suy ra:AB + AB < BE + ME + BF - MF (1)
Xét hai tam giác vuông AEM và CFM, ta có:
∠(AEM) = ∠(CFM) = 90o
AM = CM (gt)
∠(AME) = ∠(CMF) (đối đỉnh)
Suy ra: ∆AEM = ∆CFM (cạnh huyền - góc nhọn)
Suy ra: ME = MF (2)
Từ (1) và (2) suy ra: AB + AB < BE + BF
Suy ra: 2AB < BE + BF
Vậy AB < (BE + BF) / 2.
Câu 6: Cho tam giác ABC cân tại A, điểm D nằm giữa B và C. Chứng minh rằng độ dài AD nhỏ hơn cạnh bên của tam giác ABC.
Lời giải:
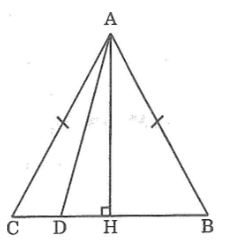
Kẻ AH ⊥ BC.
* Trường hợp H trùng với D
Ta có AH < AC (đường vuông góc ngắn hơn đường xiên)
Suy ra: AD < AC
* Trường hợp H không trùng với D
Giả sử D nằm giữa H và C.
Ta có: HD < HC
Suy ra: AD < AC (hình chiếu nhỏ hơn thì có đường xiên nhỏ hơn)
Vậy AD nhỏ hơn cạnh bên của tam giác cân ABC.
Câu 7: Cho hình sau trong đó AB > AC. Chứng minh rằng EB > EC.
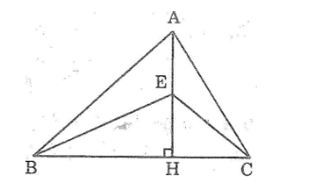
Lời giải:
Ta có: AB > AC (gt)
Suy ra: HB > HC (đường xiên lớn hơn có hình chiếu lớn hơn)
Suy ra: EB > EC (hình chiếu lớn hơn thì có đường xiên lớn hơn)
Câu 8: Cho hình sau, chứng minh rằng: BD + CE < AB + AC
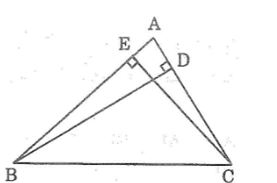
Lời giải:
Trong ΔABD, ta có ∠(ADB) = 90o
Suy ra: BD < AB (đường vuông góc ngắn hơn đường xiên) (1)
Trong ΔAEC, ta có ∠(AEC) = 90o
Suy ra: CE < AC (cạnh huyền lớn hơn cạnh góc vuông) (2)
Cộng từng vế (1) và (2), ta có: BD + CE < AB + AC.







