Giải bài tập SBT Toán 7 bài 9: Tính chất ba đường cao của tam giác

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 9: Tính chất ba đường cao của tam giác được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 7: Tính chất đường trung trực của một đoạn thẳng

Giải bài tập SBT Toán 7 bài 8: Tính chất ba đường trung trực của tam giác

Giải bài tập SBT Toán 7 bài: Ôn tập chương III

Câu 1: Cho tam giác ABC vuông tại B. Điểm nào là trực tâm của tam giác đó?

Lời giải:

Vì tam giác ABC vuông tại B nên AB ⊥ BC.

Suy ra AB là đường cao kẻ từ đỉnh A và CB là đường cao kẻ từ đỉnh C.

Vì B là giao điểm của 2 đường cao AB và CB nên B là trực tâm của tam giác ABC.

Câu 2: Cho hình bên

a, Chứng minh: CI ⊥ AB

b, Cho ∠(ACB)= 40o. Tính ∠(BID), ∠(DIE).

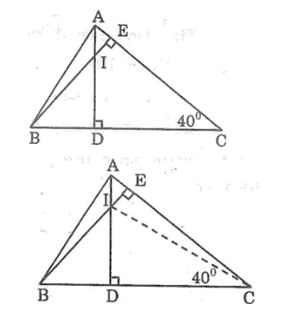
Lời giải:

a, Trong ΔABC ta có hai đường cao AD và BE cắt nhau tại I nên I là trực tâm của ΔABC

Suy ra: CI là đường cao thứ ba.

Vậy CI ⊥ AB.

b, Trong tam giác BEC có ∠(BEC)= 90^o

⇒ ∠(EBC) + ∠C= 90^o (tính chất tam giác vuông)

⇒ ∠(EBC)= 90^o - ∠C= 90^o - 40^o = 50^o hay ∠(IBD)= 50^o

Trong tam giác vuông IDB có ∠(IDB) = 90^o

⇒ ∠(IBD) + ∠(BID)= 90o (tính chất tam giác vuông)

⇒ ∠(BID) = 90^o - ∠(IBD) = 90^o - 50^o = 40^o

Mà ∠(BID) + ∠(DIE) = 180^o (2 góc kề bù)

Nên ∠(DIE)= 180^o - ∠(BID)= 180^o - 40^o = 140^o.

Câu 3: Cho H là trực tâm của tam giác ABC không vuông. Tìm trực tâm của các tam giác HAB, HAC, HBC.

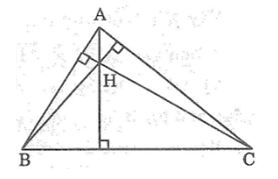
Lời giải:

Trong ∆ABC ta có H là trực tâm nên:

AH ⊥ BC, BH ⊥ AC, CH ⊥ AB

Trong ∆AHB, ta có:

AC ⊥ BH

BC ⊥ AH

Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.

Trong ∆HAC, ta có:

AB ⊥ CH

CB ⊥ AH

Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ∆HAC.

Trong ∆HBC, ta có:

BA ⊥ HC

CA ⊥ BH

Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

Câu 4: Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng đó là tam giác cân

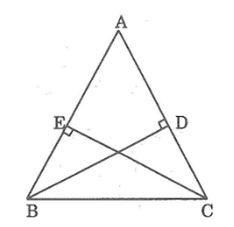
Lời giải:

Xét hai tam giác vuông BDC và CEB, có:

∠(BDC) = ∠(CEB) = 90o

BD = CE (gt)

BC cạnh huyền chung

Suy ra: ΔBDC = ΔCEB

(cạnh huyền, cạnh góc vuông)

Suy ra: ∠(DCB) = ∠(EBC)

(hai góc tương ứng bằng nhau)

Hay ∠(ACB) = ∠(ABC)

Vậy ΔABC cân tại A.

Câu 5: Cho tam giác ABC vuông tại A, đường cao AH. Tìm trực tâm của tam giác ABC, AHB, AHC.

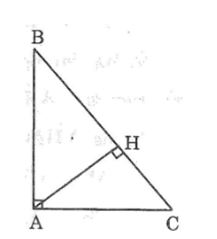
Lời giải:

*Tam giác ABC có (BAC) = 90^o

Vì CA là đường cao xuất phát từ đỉnh B nên giao điểm của hai đường này là A.

Vậy A là trực tâm của ΔABC.

*Tam giác AHB có (AHB) = 90^o

Vì AH là đường cao xuất phát từ đỉnh A, BH là đường cao xuất phát từ đỉnh B nên giao điểm của hai đường này là H.

Vậy H là trực tâm của ΔAHB.

*Tam giác AHC có (AHC) = 90^o

Vì AH là đường cao xuất phát từ đỉnh A, CH là đường cao xuất phát từ đỉnh C nên giao điểm của hai đường này là H.

Vậy H là trực tâm của ΔAHC.

Câu 6: Cho hình dưới. Có thể khẳng định rằng các đường thẳng AC, BD, KE cùng đi qua một điểm hay không? Vì sao?

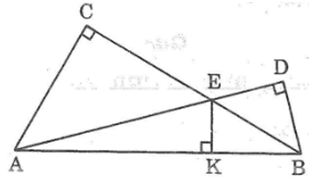
Lời giải:

Trong ΔAEB, ta có: AC ⊥ EB

Suy ra AC là đường cao xuất phát từ đỉnh A.

Trong ΔAEB, ta có: BD ⊥ AE

Suy ra BD là đường cao xuất phát từ đỉnh B.

Trong ΔAEB, ta có: EK ⊥ AB

Suy ra EK là đường cao xuất phát từ đỉnh E

Theo tính chất ba đường cao trong tam giác nên các đường thẳng AC, BD và EK cùng đi qua một điểm.

Câu 7: Cho tam giác ABC cân tại A, đường trung tuyến AM. Qua A kẻ đường thẳng d vuông góc với AM. Chứng minh rằng d song song với BC.

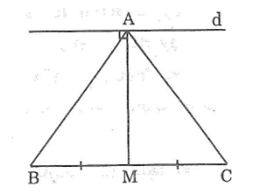
Lời giải:

Vì ΔABC cân tại A và AM là đường trung tuyến nên AM cũng là đường cao

Ta có: AM ⊥ BC

d ⊥ AM (gt)

Vì hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song nhau nên ta có: d // BC.

Câu 8: Cho tam giác ABC cân tại A. Vẽ điểm D sao cho A là trung điểm của BD. Kẻ đường cao AE của ∆ABC, đường cao AF của ∆ACD. Chứng minh rằng ∠(EAF) = 90^o.

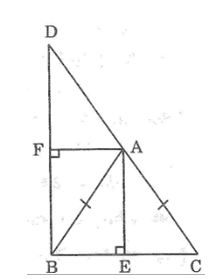
Lời giải:

Ta có: ΔABC cân tại A

AE ⊥ BC (gt)

Vì AE là đường cao của tam giác ABC nên AE cũng là đường phân giác của ∠(BAC)

Lại có: ΔADB cân tại A

AF ⊥ BD (gt)

Vì AF là đường cao nên AF cũng là đường phân giác của ∠(BAD)

Mà ∠(BAC) và ∠(BAD) là hai góc kề bù nên: AE ⊥ AF.

Câu 9: Cho tam giác ABC cân tại A, đường cao CH cắt tia phân giác của góc A tại D. Chứng minh rằng BD vuông góc với AC.

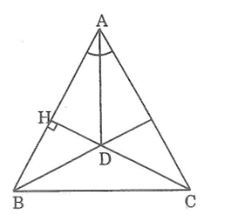
Lời giải:

Vì ΔABC cân tại A nên đường phân giác của góc ở đỉnh A cũng là đường cao từ A.

Suy ra: AD ⊥ BC

Ta có: CH ⊥ AB (gt)

Tam giác ABC có hai đường cao AD và CH cắt nhau tại D nên D là trực tâm của ∆ABC

Suy ra BD là đường cao xuất phát từ đỉnh B đến cạnh AC.

Vậy BD ⊥ AC.

Câu 10: Tam giác ABC có AB = AC = 13cm, BC = 10cm. Tính độ dài đường trung tuyến AM.

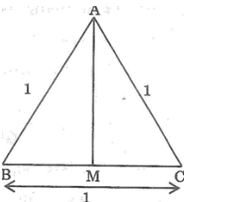
Lời giải:

Vì tam giác ABC cân tại A nên đường trung tuyến AM cũng là đường cao.

Suy ra: AM ⊥ BC

Ta có: MB = MC = 1/2 BC = 1/2 .10 = 5 (cm)

Trong tam giác vuông AMB có (AMB) = 90^o

Áp dụng định lý Pitago ta có:

AB² = AM² + MB²

Suy ra: AM² = AB² - MB²

= 13² - 5² = 169 - 25 = 144

Vậy AM = 12 (cm)