Giải bài tập SBT Toán 7 bài: Ôn tập chương III

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài: Ôn tập chương III được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 7: Tính chất đường trung trực của một đoạn thẳng

Giải bài tập SBT Toán 7 bài 8: Tính chất ba đường trung trực của tam giác

Giải bài tập SBT Toán 7 bài 9: Tính chất ba đường cao của tam giác

Câu 1: Cho tam giác ABC có AB < AC. Trên tia đối của tia BC lấy điểm M sao cho BM = BA. Trên tia đối của tia CB lấy điểm N sao cho CN = CA.

a, Hãy so sánh các góc AMB và ANC.

b, Hãy so sánh các độ dài AM và AN.

Lời giải:

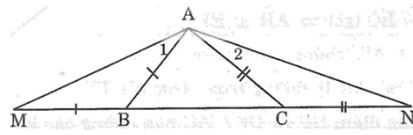
a, Trong ΔABC, ta có AB < AC

Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)

Ta có: AB = BM (gt) ⇒ ΔABM cân tại B

Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)

Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B

Suy ra: ∠(ABC) = ∠(AMB) + ∠A1

Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)

Lại có: AC = CN (gt) ⇒ ΔACN cân tại C

Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)

Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C

Suy ra: ∠(ACB) = ∠(ANC) + ∠A2

Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)

Từ (1), (2) và (3) suy ra: (AMB) > ∠(ANC) .

b, Trong ΔAMN, ta có: (AMB) > (ANC)

Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

Câu 2: Cho tam giác ABC có AB < AC, đường cao AH. Chứng minh rằng: HB < HC, ∠(HAB) < ∠ (HAC)(xét hai trường hợp: B nhọn và B tù).

Lời giải:

Ta có: AB < AC (gt)

Suy ra: HB < HC (đường xiên lớn hơn thì hình chiếu lớn hơn)

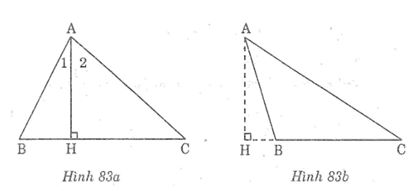
* Trường hợp B nhọn (hình 83a)

Trong Δ ABC, ta có: AB < AC

Suy ra: ∠B > ∠C (đối diện với cạnh lớn hơn là góc lớn hơn)

Trong Δ AHB, ta có ∠(AHB) = 90^o

Suy ra: ∠B + ∠(HAB) = 90^o (tính chất tam giác vuông) (1)

Trong Δ AHC, ta có ∠(AHC) = 90^o

Suy ra: ∠C + ∠(HAC) = 90o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B + ∠(HAB) = ∠C + ∠(HAC)

Mà ∠B > ∠C nên ∠(HAB) < ∠(HAC)

* Trường hợp B tù (hình 83b)

Vì điểm B nằm giữa H và C nên ∠(HAC) = ∠(HAB) + ∠(BAC)

Vậy ∠(HAB) < ∠(HAC).

Câu 3: Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài 1cm, 2cm, 3cm, 4cm, 5cm.

Lời giải:

Ta có: 1 = 3 - 2 = 4 - 3 = 5 - 4

Suy ra: trong 3 cạnh của tam giác không có cạnh nào có độ dài 1cm.

* Nếu cạnh nhỏ nhất là 2cm

Ta có: 4 - 3 < 2 < 4 + 3; 5 - 4 < 2 < 5 + 4

Suy ra: hai cạnh kia là 3cm và 4cm hoặc 4cm và 5cm

* Nếu cạnh nhỏ nhất là 3cm

Ta có: 5 - 4 < 3 < 5 + 4; 3 = 5 - 2; 3 > 4 - 2

Như vậy hai cạnh kia là 5cm và 4cm

* Không có trường hợp cạnh nhỏ nhất là 4cm

Vậy có thể vẽ được ba tam giác với độ dài các cạnh là:

2cm; 3cm; 4cm

2cm; 4cm; 5cm

3cm; 4cm; 5cm

Câu 4: Cho bốn điểm A, B, C, D như hình bên. Hãy tìm một điểm M sao cho tổng MA + MB + MC + MD là nhỏ nhất.

Lời giải:

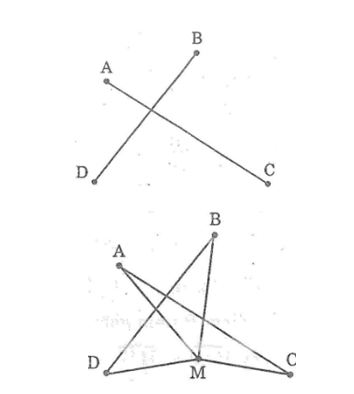
* Nếu M không trùng với giao điểm của AC và BD

Trong ΔAMC, ta có: MA + MC > AC (bất đẳng thức tam giác)

Trong ΔMBD, ta có: MB + MD > BD (bất đẳng thức tam giác)

* Nếu M trùng với giao điểm AC và BD

Ta có: MA + MC = AC

MB + MD = BD

Suy ra: MA + MC ≥ AC

MB + MD ≥ BD (dấu bằng xảy ra khi M trùng với giao điểm của AC và BD)

Suy ra: MA + MB + MC + MD ≥ AC + BD

Vậy MA + MB + MC + MD = AC + BD bé nhất khi đó M là giao điểm của AC và BD.

Câu 5: Cho hình sau trong đó G la trọng tâm của tam giác ABC. Chứng minh rằng:

1. S_AGC= 2S_GMC
2. S_GMB= S_GMC
3. S_AGB= S_AGC= S_BGC

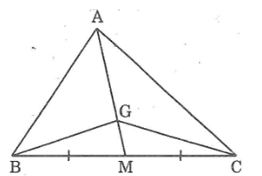
Lời giải:

a, Vì G là trung điểm của ΔABC nên GA = 2GM (tính chất đường trung tuyến)

Ta có ΔAGC và ΔGMC có chung đường cao kẻ từ đỉnh C đến AM, đồng thời cạnh đáy GA = 2GM.

Suy ra: S_AGC = 2S_GMC (1)

b, Ta có ΔGMB và ΔGMC có cạnh đáy MB = MC, chung đường cao kẻ từ đỉnh G đến cạnh BC

Suy ra: SGMB = SGMC (2)

c, Ta có ΔAGB và ΔGMB có chung đường cao kẻ từ đỉnh B đến cạnh AM, đồng thời AG = 2GM (chứng minh trên)

Suy ra: S_AGB = 2S_GMB (3)

Mà S_BGC = S_GMB + S_GMC = 2S_GMB (4)

Từ (1), (2), (3) và (4) suy ra: S_AGB = S_AGC = S_BGC

Câu 6: Cho góc xOy khác góc bẹt, điểm A thuộc cạnh Ox, điểm B thuộc cạnh Oy.

a, Hãy tìm điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy)

b, Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?

Lời giải:

a, Vì điểm M nằm trong góc xOy và cách đều hai cạnh Ox và Oy nên M thuộc tia phân giác Oz của ∠(xOy).

Vì điểm M cách đều 2 điểm A và B nên M thuộc đường trung trực của AB.

Vậy M là giao điểm của đường trung trực của đoạn thẳng AB và tia phân giác ∠(xOy)

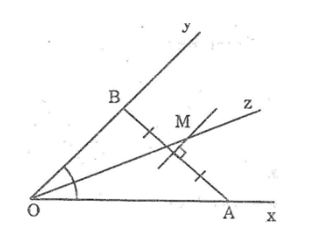
b, Nếu OA = OB thì ΔOAB cân tại O

Khi đó tia phân giác của ∠(xOy) cũng là đường trung trực của AB

Vậy bất kì điểm M nào nằm trên tia phân giác của ∠(xOy) đều thỏa mãn điều kiện trong câu a).

Câu 7: Cho góc xOy khác góc bẹt. Dùng một chiếc thước thẳng có chia khoảng, hãy nêu cách vẽ tia phân giác của góc xOy.

Lời giải:

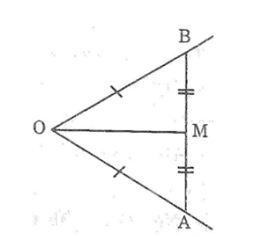
- Dùng thước chia khoảng, trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = OB.

- Nối AB.

- Dùng thước chia khoảng để đo đoạn AB, lấy trung điểm M của AB.

- Kẻ tia OM.

Vì tam giác OAB cân tại O và OM là đường trung tuyến nên OM cũng là đường phân giác của ∠(AOB).

Vậy OM là tia phân giác của ∠(xOy).

Câu 8: Cho hình dưới trong đó giao điểm O của hai đường thẳng a và b nằm ngoài phạm vi tờ giấy. Chỉ vẽ hình trong phạm vi tờ giấu, hãy vẽ đường thẳng d đi qua A sao cho đường thẳng d cũng đi qua O nếu kéo dài đường thẳng d ra ngoài phạm vi tờ giấy.

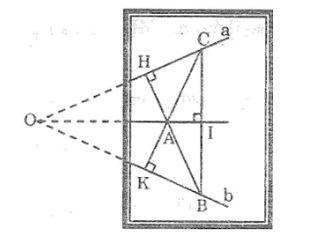
Lời giải:

- Kẻ AH ⊥ a kéo dài HA cắt b tại B

- Kẻ AH ⊥ b kéo dài KA cắt a tại C

- Kẻ AI ⊥ BC, đường thẳng AI đi qua O

Vì tam giác OBC có hai đường cao BH và CK cắt nhau tại A nên A là trực tâm của tam giác OBC.

Khi đó OA là đường cao thứ ba nên OA ⊥ BC.

Vì AI ⊥ BC nên đường thẳng OA và đường thẳng AI trùng nhau hay đường thẳng AI đi qua O.

Câu 9: Đường trung trực d của đoạn thẳng AB chia mặt phẳng thành hai phần (không kể đường thẳng d): phần chứa điểm A ký hiệu là PA, phần chứa điểm B ký hiệu là PB (hình bên).

a, Gọi M là một điểm của PA. Chứng minh rằng MA < MB

b, Gọi N là một điểm của PB. Chứng minh rằng NB < NA

c, Gọi K là một điểm sao cho KA < KB. Hỏi rằng K nằm ở đâu: trong PA, PB hay trên d?

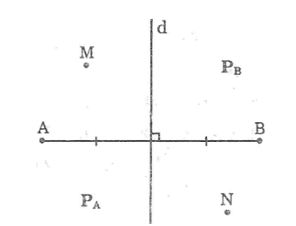
Lời giải:

a, Nối MA, MB. Gọi C là giao điểm của MB với đường thẳng d, nối CA.

Ta có: MB = MC + CB

mà CA = CB (tính chất đường trung trực)

Suy ra: MB = MC + CA (1)

Trong ΔMAC ta có:

MA < MC + CA (bất đẳng thức tam giác) (2)

Từ (1) và (2) suy ra: MA < MB

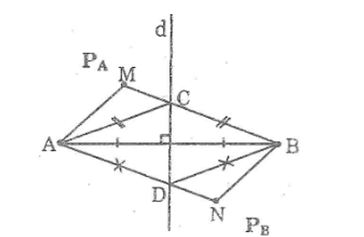
b, Nối NA, NB. Gọi D là giao điểm của NA với đường thẳng d, nối DB.

Ta có: NA = ND + DA

mà DA = DB (tính chất đường trung trực)

Suy ra: NA = ND + DB (3)

Trong ΔNDB, ta có:

NB < ND + DB (bất đẳng thức tam giác) (4)

Từ (3) và (4) suy ra: NA > NB

c, Theo câu a), ta có: MA < MB

Mà M là một điểm của PA nên K là một điểm của PA.