Giải bài tập SBT Toán 7 bài 1: Tổng ba góc của một tam giác

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 1: Tổng ba góc của một tam giác được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 6: Từ vuông góc đến song song

Giải bài tập SBT Toán 7 bài 7: Định lí

Giải bài tập SBT Toán 7 bài 2: Hai tam giác bằng nhau

Câu 1: Tính giá trị x ở hình dưới:

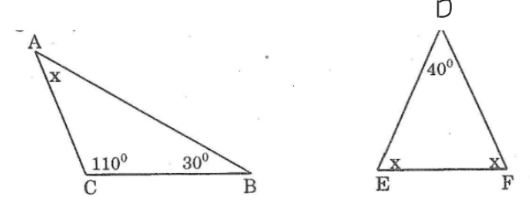
Lời giải:

Trong ΔABC ta có:

∠A +∠B +∠C =180o(tổng ba góc trong tam giác)

∠A =180^o-(∠B +∠C)

x=180^o-(30^o+110^o)=40

Trong ΔDEF có:

∠D +∠E +∠F =180^o (tổng ba góc trong tam giác)

Mà ∠E =∠F (gt)

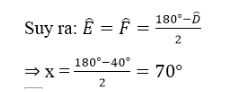
Câu 2: Cho tam giác ABC có ∠A =60^o, ∠C =50^o. Tia phân giác của góc B cắt AC ở D. Tính ∠ADB, ∠CDB

Lời giải:

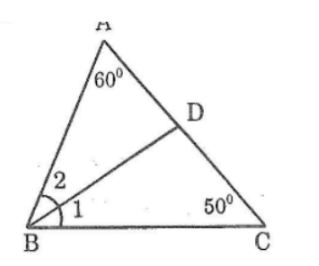
Trong ΔABC ta có:

∠A +∠B +∠C =180^o(tổng ba góc trong tam giác)

⇒∠B =180^o-(∠A +∠C)

⇒x = 180^o-(60^o+50^o) = 70^o

(∠B1) =(∠B2 ) =(1/2 )∠B (vì BD là tia phân giác)

⇒∠B =70^o:2=35^o

Trong ΔBCD ta có ∠(ADB) là góc ngoài tại đỉnh D

⇒ ∠(ADB) =∠(B1 ) +∠C (tính chất góc ngoài tam giác)

∠(ADB) +∠(BDC) =180^o(hai góc kề bù)

⇒∠(BDC) =180^o-∠(ADB) =180^o-85^o=95^o

Câu 3: Cho tam giác ABC, điểm M nằm trong ta, giác đó. Tia BM cắt AC ở K.

So sánh ∠(AMK) và ∠(ABK)

So sánh ∠(AMC) và ∠(ABC)

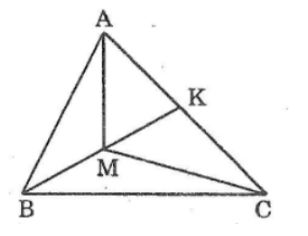
Lời giải:

Trong ΔAMB ta có AMK là góc ngoài tại đỉnh M.

⇒ ∠(AMK) > ∠(ABK) (tính chất góc ngoài tam giác) (1)

Trong ΔCBM ta có KMC là góc ngoài tại đỉnh M

⇒∠(KMC) > ∠(MBC) (tính chất góc ngoài tam giác) (2)

Cộng từng vế (1) và (2) ta có: ∠(AMK) +∠(KMC) > ∠(ABM) +∠(MBC)

Suy ra: ∠(AMC) > ∠(ABC)

Câu 4: Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc AC). Hãy so sánh ∠(ABH) và ∠(ACK)

Lời giải:

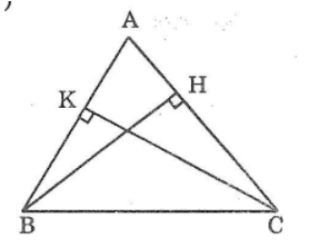
Tam giác nhọn ABH bvuông tại H

⇒ ∠(ABH) +∠A =90^o (tính chất tam giác vuông)

⇒∠(ABH) =90^o - ∠A (1)

Tam giác AC vuông tại K

⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)

⇒∠(ACK) =90^o-∠A (2)

từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)

Câu 5: Cho tam giác ABC có ∠B =∠C =50^o. Gọi Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ rằng Am // BC.

Lời giải:

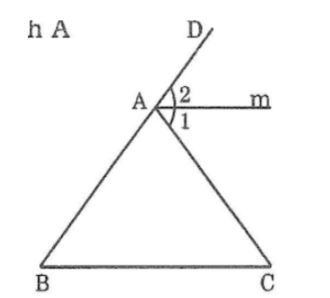
Trong Δ ABC có ∠(CAD ) là góc ngoài đỉnh A

⇒∠(CAD ) =∠B +∠C =50+50=100^o

(tính chất góc ngoài tam giác)

∠(A1 ) =∠(A2 ) =1/2 ∠(CAD) =50^o (vì tia Am là tia phân giác của ∠(CAD)

Suy ra: ∠(A1) =∠C =50^o

⇒ Am // BC (vì có cặp góc ở vị trí so le trong bằng nhau)

Câu 6: a, Một góc nhọn của eke bằng 30o. Tính góc nhọn còn lại.

b, Một góc nhọn của eke bằng 45o.tính góc nhọn còn lại

Lời giải:

Vì eke là một tam giác vuông , nên:

Một góc nhọn của eke bằng 30o thì góc còn lại bằng:

90^o- 30^o= 60^o

Một góc nhọn của eke bằng 45o thì góc còn lại bằng:

90^o - 45^o= 45^o

Câu 7: Cho tam giác ABC có ∠A =100o,∠B -∠C =20^o. Tính ∠B và∠ C

Lời giải:

Trong ΔABC, ta có:

∠A +∠B +∠C =180^o (tổng ba góc trong tam giác)

∠B -∠C =20^o (2)

Từ (1) và (2) suy ra: 2B =100^o⇒B =50^o

Vậy: ∠C =80^o-50^o=30^o

Câu 8: Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H thuộc BC). Tìm góc B.

Lời giải:

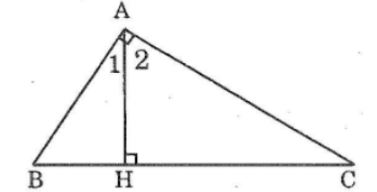
Có thể tìm góc B bằng hia cách:

Cách 1

Ta có: ∠(A1) +∠(A2) =∠(BAC) =90^o (1)

Vì ΔAHB vuông tại H nên:

∠B +∠(A1) =90^o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra ∠B =∠(A2)

Cách 2

Vì ΔABC vuông tại A nên:

∠B +∠C =90^o (theo tính chất tam giác vuông) (1)

Vì ΔAHC vuông tại H nên:

∠(A2) +∠C =90^o (tính chất tam giác vuông) (2)

Từ (1) và (2) suy ra: ∠B =∠(A2)

Câu 9: Cho tam giác ABC có ∠B =70^o; ∠C =30^o. Tia phân giác của góc A cắt BC tại D. kẻ AH vuông góc vói BC (H thuộc BC)

Tinh ∠(BAC)

Tính ∠(ADH)

Tính ∠(HAD)

Lời giải:

Trong ΔABC có:

∠(BAC) +∠B +∠C =180^o (tổng ba góc trong tam giác)

Mà ∠(BAC) +70^o+30^o=180

Vậy ∠(BAC) =180^o-70^o-30^o=80^o

Ta có: ∠(A1) =(1/2)∠(BAC) =(1/2).80^o=40^o

(vì Ad tia phân giác của góc BAC)

Trong ΔADC ta có ∠(ADH) là góc ngoài tạ đỉnh D

Do đó: ∠(ADH) =∠(A1) +∠C (tính chất góc ngoài của tam giác)

Vậy ∠(ADH) =40^o+30^o=70^o

ΔADH vuông tại H nên:

∠(HAD) +∠(ADH) =90^o (tính chất tam giác vuông)

⇒∠ (HAD) =90^o-∠(ADH)o=90^o-70^o=20^o

Câu 10: Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. tính (BIC) ̂biết rằng:

∠B =80^o,∠C =40^o

∠A =80^o

∠A =m^o

Lời giải:

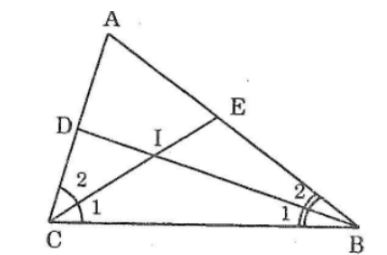
Ta có:

∠(B1) =(1/2)∠(ABC) =(1/2).80^o=40^o (vì BD là tia phân giác ∠(ABC))

∠(C1) =(1/2)∠(ACB) =(1/2).20^o=10^o (vì CE là tia phân giác∠ (ACB))

Trong ΔIBC, ta có: ∠(BIC) +∠(B1) +∠(C1) =180o(tổng 3 góc trong tam giác)

Vậy: ∠(BIC) =180o-(∠(B1) +∠(C1))=180^o-(40^o+20^o)=120^o

Ta có:

∠(B1) =(1/2)∠ B (vì BD là tia phân giác B)

∠(C1) =(1/2)C (vì CE là tia phân giác∠(C))

Trong ΔABC có:

∠(BIC) +∠(B1) +∠(C1) =180^o (tổng ba goác trong tam giác)

Vậy ∠(BIC) =180^o-((B) +∠(C1))=180^o-(∠B +∠C)/2=180^o-(100^o)/2=130^o

Ta có:∠B +∠C =180^o-m^o

Suy ra: ∠(BIC) =180^o-(180^o-m^o)/2=180-90^o+(m^o)/2=90^o+ (1/2)m^o

Câu 11: Trên hình bên có Ax song sog với By, ∠(CAx) =50^o,∠(CBy) =40^o. Tính ∠(ACB) bằng cách xem nó là góc ngoài của một tam giác.

Lời giải:

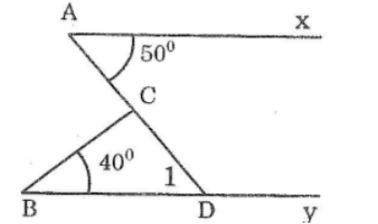
Kéo dài AC cắt By tại D

Vì By // Ax suy ra ∠(D1) =∠A (hai góc so le trong)

Mà ∠A =50^o(gt) nên ∠(D1) =50^o

TrongΔBCD ta có ∠(ACB) là góc ngoài tại đỉnh C

⇒∠(ADC) =∠B +∠(D1) (tính chất góc ngoài của tam giác)

⇒∠(ADC) =40^o+50^o=90^o

Câu 12: Chứng minh rằng tổng ba goc ngoài ở ba đỉnh của một tam giác thì bằng 360

Lời giải:

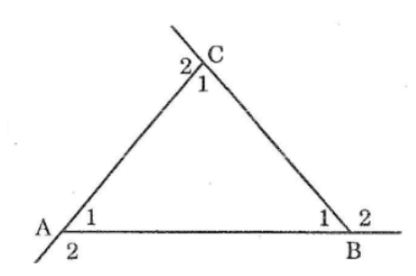
Ta có: ∠(A1) +∠(A2) =180^o(hai goác kề bù)

∠(B1) +∠(B2) =180^o(hai goác kề bù)

∠(C1) +∠(C2)=180^o(hai goác kề bù)

Suy ra: ∠(A1) +∠(A2) +∠(B1) +∠(B2) +∠(C1) +∠(C2) =180.3=540^o

⇒∠(A2) + ∠( B2) +∠(C2) =540^o-(∠(A1) +∠(B1) +∠(C1)) (1)

Trong ΔABC, ta có:

∠(A1) +∠(B1) +∠(C1) =180^o (tổng ba góc trong tam giác) (2)

Từ (1) và (2) suy ra: ∠(A2) +∠(B2) +∠(C2) =540^o-180^o=360^o