Giải bài tập SBT Toán 7 bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 1: Tổng ba góc của một tam giác

Giải bài tập SBT Toán 7 bài 2: Hai tam giác bằng nhau

Giải bài tập SBT Toán 7 bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

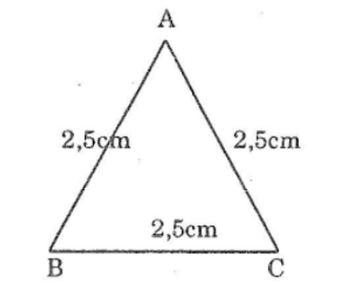
Câu 1: Vẽ tam giác ABC biết độ dài mỗi cạnh bằng 2,5cm. Sau đó đo mỗi góc của tam giác.

Lời giải:

Ta có: AB=AC=BC=2,5cm

Suy ra: ΔABC đều

Vậy:∠ A =∠B =∠C =60^o

Câu 2: Cho hai tam giác ABC và ABH có AB = BC = CA = 3cm, AD = BD = 2cm (C và D nằm khác phía đối với AB)

Chứng minh rằng: ∠(CAD) =∠(CBD)

Lời giải:

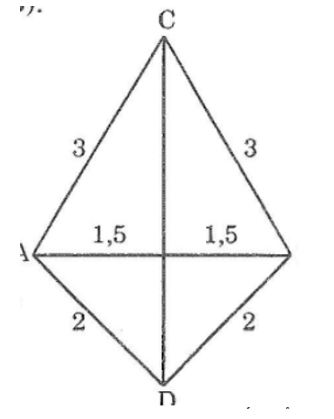
Xét ΔCAD và ΔCBD, ta có:

AC = BC (gt)

AD = BD (gt)

Cd cạnh chung

Suy ra: ΔCAD= ΔCBD(c.c.c)

Vậy ∠ (CAD) =∠ (CBD) ̂(hai góc tương ứng)

Câu 3: Cho góc xOy. Trên tia Ox lấy điểm C, trên tia Oy lấy điểm D sao cho OD = OC. Vẽ các cung tròn tâm C và tâm D có cùng bán kính sao cho chúng cắt nhau tại E nằm trong xOy. Chứng minh rằng OE là tia phân giác của góc xOy

Lời giải:

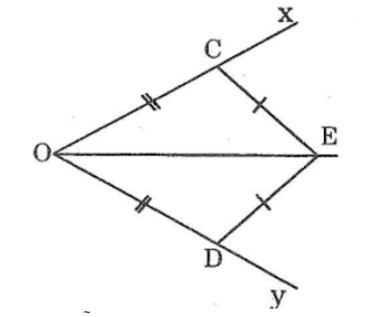
Xét ΔCOE và ΔDOE. Ta có:

OE cạnh chung

OD = OC (bán kính của 1 cung tròn)

DE=CE (bán kính 2 cung tròn bằng nhau)

Suy ra: ΔCOE= ΔDOE(c.c.c)

Vậy: ∠(COE) = ∠(DOE) ̂(hai góc tương ứng)

Vì OE nằm giữa OC và OD nên OE là tia phân giác cua goác DOC hay OE là tia phân giác của góc xOy

Câu 4: Tìm chỗ sai trong bài làm sau đây của một học sinh (hình bên)

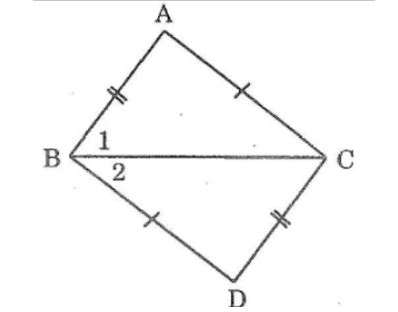
ΔABC=ΔDCB (c.c.c)

∠ (B_1 ) =∠ (B_1) ̂(cặp góc tương ứng)

⇒ BC là tia phân giác của góc ABD

Lời giải:

Bạn học sinh suy luận ΔABC=ΔDCB

⇒ ∠(B_1) =∠ (B_1) ̂là sai vì ⇒∠(B_1) và ∠(B_1) ̂không phải là 2 góc tương ứng của hai tam giác bằng nhau nói trên. Do ssos không suy luận ra được BC là tia phân giác của góc ABD

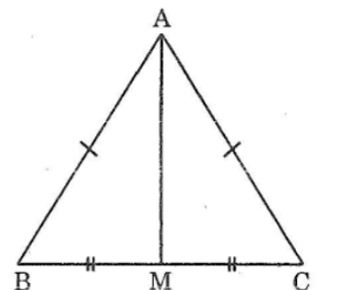
Câu 5: Tam giác ABC có AB = Ac, M là trung điểm của BC. Chứng minh rằng AM vuông góc với BC.

Lời giải:

Xét ΔAMB và ΔAMC, ta có:

AB = AC (gt)

BM = CM (vì M là trung điểm BC)

AM cạnh chung

Suy ra: ΔAMB= ΔAMC(c.c.c)

⇒∠ (AMB) =(AMC) ̂(hai góc tương ứng)

Ta có: ∠(AMB) +∠(AMC) =180^o (hai góc kề bù)

∠(AMB) =∠(AMC) =90^o. Vậy AM ⏊ BC

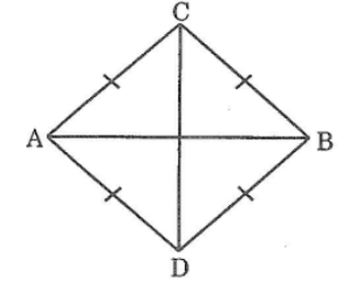
Câu 6: Cho đoạn thẳng AB. Vẽ cung tròn tâm A bán kính AB và cung tròn tâm B bán kinh BA, chúng cắt nhau ở C và D. chứng inh rằng:

a, ΔABC= ΔABD

b, ΔACD= ΔBCD

Lời giải:

a, Xét ΔABC và ΔABD, ta có:

AC = AD (bán kính (A))

Ab cạnh chung

BC = BD (bán kính (B))

Suy ra: ΔABC= ΔABD

b, Xét ΔACD= ΔBCD, ta có:

AC = BC (bán kính hai đường tròn)

CD cạnh chung

AD = BD (bán kính hai đường tròn)

Suy ra: ΔACD= ΔBCD(c.c.c)

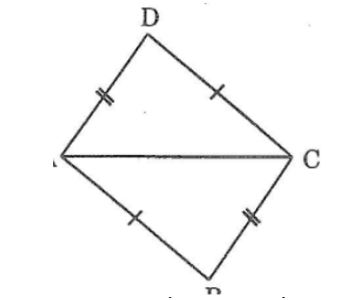
Câu 7: Cho tam giác ABC. Vẽ cung tròn tâm A bán kính BC, vẽ cung tròn tâm C bán kính BA, chúng cắt nhau tại D ( D và B nằm khác phí đối với AC). Chứng minh rằng AD // BC

Lời giải:

Xét ΔABC và ΔCDA, ta có:

AB = CD (theo cách vẽ)

AC cạnh chung

BC = AD (theo cách vẽ)

Suy ra: ΔABC= ΔCDA (c.c.c) ⊥∠(ACB) =∠(CAD)

Vậy AD // BC (vì cáo cặp góc so le trong bằng nhau)

Câu 8: Cho đường thẳng xy, các điểm B và C nằm trên xy, điểm A nằm ngoài xy. Dựa vào bài 34, hãy nêu cách vẽ đường thẳng đi qua A và song song với BC.

Lời giải:

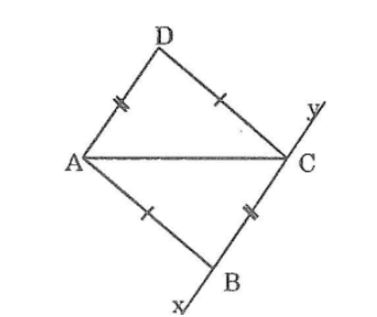
Nối AB, nửa mặt phẳng bờ BC có chứa A. Vẽ cung tròn tâm A bán kính bằng BC. Vẽ cung tròn tâm C bán kính bằng AB. Hai cung tròn cắt nhau tại D.

Kẻ đường thẳng AD ta có AD // xy