Giải bài tập SBT Toán 7 bài 7: Định lí Pi-ta-go

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 7: Định lí Pi-ta-go được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc

Giải bài tập SBT Toán 7 bài 6: Tam giác cân

Giải bài tập SBT Toán 7 bài 8: Các trường hợp bằng nhau của tam giác vuông

Câu 1: Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm

Lời giải:

Giả sử ∆ABC có ∠A =90^o, BC = 13 cm, AC = 12cm

Theo định lý pitago ta có: BC² = AB²=AC²

Suy ra: AB²=BC²-AC²=13²-12²=25

Vậy AB = 5 cm

Câu 2: Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC= 20vm, AH = 12 cm và BH = 5cm

Lời giải:

∆AHB có (AHB) =90°

Theo định lý pitago, ta có:

AB²=AH²+HB²

= 12²+5²=169

Vậy AB = 13 cm

∆AHC có (AHC) =90^o

Theo định lý pitago, ta có:

AC²=AH²+HC²

HC²=AC²-AH²=20²-12²=400-144=256

Vậy HC = 16cm

Ta có: BC = BH + HC = 5 +16 = 21cm

Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

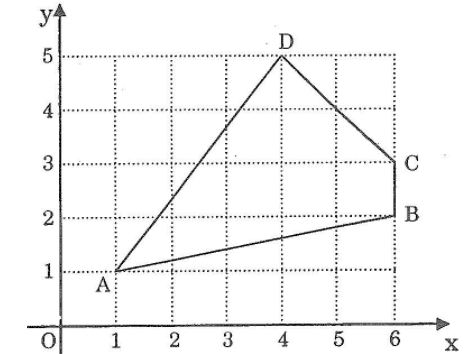
Câu 3: Tính độ dài các đoạn thẳng AB, BC, CD và Da trên hình dưới.

Lời giải:

Theo định lí pitago ta có:

AB² = 5²+1²=25+1=26 => AB =√ 26

CD²=2²+2²=4+4=8 =>CD =√ 8

AD²=3²+4²=9+14=25 =>AD = 5

Và BC = 1

Câu 4: Màn hình của một máy thu hình có dạnh hình chữ nhật, chiều rộng 12 inh-sơ, đường chéo 20 inh-sơ. Tính chiều dài

Lời giải:

Giả sử màn hình máy thu hình là hình chữ nhật ABCD, chều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD.

Ta có tam gác ABD vuông tại A

Theo định lí pitago ta có: BD²=AB²+AD²

⇒ AB²=BD² –AD²=20²-12²=400-144=256

Vậy AB = 16 inh-sơ

Câu 5: Tính đường chéo của một mặt bàn hình chữ nhật có chiều dài 10dm, chiều rộng 5dm

Lời giải:

Giả sử mặt bàn hình chữ nhật ABCD, chiều rộng BC = AD, chiều dài AB = CD, đường chéo AC = BD

Ta có tam giác ABD vuông tại A.

Theo định lí pita go ta có: BD²=AB²+AD²

BD²=10²+ 2=100+25=125

Vậy: BD = √125=25dm

Câu 6: Hai đoạn thẳng AC, BD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn thẳng. Tính các độ dài AB, BC, CD, DA biết AC = 12 cm; BD = 16cm

Lời giải:

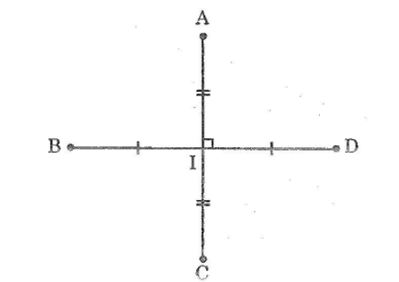
Gọi I là giao điểm của AC và BD

Ta có: IA = IC = AC/2=6cm

IB = ID = BD/2=8cm

Áp dụng định lí pitago vào tam giác vuông AIB ta có:

AB²=IA²+IB²

AB²=6²+8²=36+64=100

Vậy AB = 10 cm

Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)

Suy ra: AD = BC = CD = AB = 10cm

Câu 7: Tính độ dài các cạnh góc vuông của một tam giác vuông cân có cạnh huyền bằng:

a.2cm

b.√ 2 cm

Lời giải:

Tam giác vuông cân là tam giác vuông có 2 cạnh góc vuông bằng nhau. Gọi độ dài cạnh góc vuông là x (cm) (x > 0)

Áp dụng định lí pitago ta có:

x² + x² = 2²=> 2x=4=>x² =2=> x = √2cm

Áp dụng định lí pitago ta có:

x² +x² =(√2)2⇒ 2x² = 2 => x² =1

=> x=1cm

Câu 8: Bạn An đi từ nhà mình (a) qua nhà bạn Lan (B) rồi đên nhà bạn Châu (C) lúc trở về, An qua nhà bạn Dũng (D) rồi trở về nhà mình (hình bên). So sánh quãng đường lúc đi và quãng đường lúc về của An, quãng đường nào dài hơn.

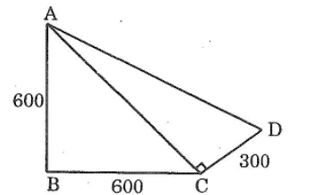
Lời giải:

Trong tam giác vuông ABC có ∠ABC =90^o

Áp dụng định lí pitago ta có:

AC²=AB²+BC²=600²+600²=360000+360000=720000

Trong tam giác vuông ACD, ta có ∠ACD =90^o

Áp dụng định lí pitago ta có:

AD²=AC²+CD²=720000+3002=720000+90000=810000

Suy ra: AD = 900m

Quãng đường ABC dài 600 + 600 = 1200m

Quãng đường CDA dài 300 + 900 = 1200m

Vậy quãng đường lúc đi và lúc về của An là bằng nhau