VnDoc.com Lớp 7 Giải SBT Toán 7

Giải SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Giải sách bài tập Toán 7
133 17.132
Tải về Bài viết đã được lưu

SBT Toán lớp 7 bài 1: Tập hợp Q các số hữu tỉ

Mời các bạn tham khảo Giải SBT Toán 7 bài 1 Tập hợp Q các số hữu tỉ được VnDoc đăng tải sau đây. Đây là lời giải hay cho các câu hỏi trong sách bài tập Toán 7 giúp các em ôn tập và củng cố kiến thức được học hiệu quả. Hy vọng đây là tài liệu hữu ích giúp các em học tốt môn Toán lớp 7 và nâng cao kỹ năng giải Toán 7. Chúc các em học tốt.

Giải bài tập SBT Toán 7 bài 2: Cộng, trừ số hữu tỉ

Câu 1 - SBT Toán 7 tr 5:

Điền kí hiệu (\in , \notin , \subset) thích hợp vào ô trống:

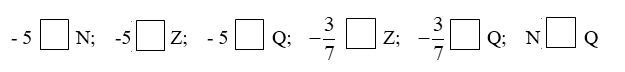
Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Lời giải:

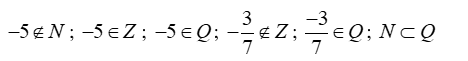
Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Câu 2 - SBT Toán 7 tr 5:

Biểu diễn các số \frac{3}{{ - 4}};\frac{5}{3} hữu tỉ:

Lời giải:

Ta có: \frac{3}{{ - 4}} = \frac{{ - 3}}{4}

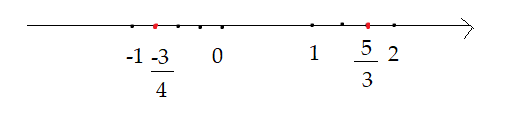
Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Câu 3 - SBT Toán 7 tr 5:

Biểu diễn các số hữu tỉ

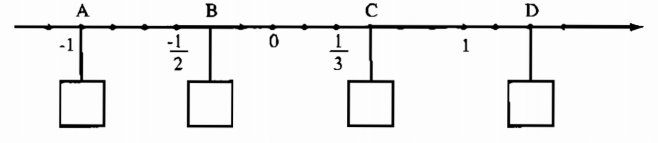
Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Lời giải:

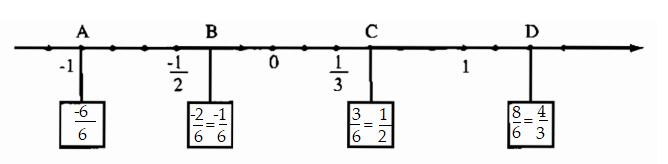
Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ

Câu 4 - SBT Toán 7 tr 5:

Trong các câu sau câu nào đúng câu nào sai”

  1. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương
  2. Số hữu tỉ âm nhỏ hơn số tự nhiên
  3. Số 0 là số hữu tỉ dương
  4. Số nguyên âm không phải là số hữu tỉ âm
  5. Tập hợp Q gồm các số hữu tỉ hữi tỉ dương và các sô hữu tỉ âm

Lời giải:

  1. Số hữu tỉ âm nhỏ hơn số hữu tỉ dươg. Đúng
  2. Số hữu tỉ âm nhỏ hơn số tự nhiên. Đúng
  3. Số 0 là số hữu tỉ dương. Sai
  4. Số nguyên âm không phải là số hữu tỉ âm. Sai
  5. Tập hợp Q gồm các số hữu tỉ hữi tỉ dương và các sô hữu tỉ âm. Sai

Câu 5 - SBT Toán 7 tr 5:

Cho hai số hữu tỉ \frac{a}{b} và \frac{c}{d}(b > 0, d> 0). Chứng tỏ rằng:

a) Nếu \frac{a}{b} < \frac{c}{d} thì ad < bc

b) Nếu ad < bc thì \frac{a}{b} < \frac{c}{d}

Lời giải:

a, Với d > 0, ta có: \frac{a}{b} = \frac{{a.d}}{{b.d}}và với b > 0, ta có: \frac{c}{d} = \frac{{b.c}}{{b.d}}

Theo đề bài \frac{a}{b} < \frac{c}{d} \Rightarrow \frac{{a.d}}{{b.d}} < \frac{{b.c}}{{b.d}} \Rightarrow ad < bc(đpcm)

b, Với b, d > 0, có:

ad < bc \Rightarrow \frac{{ad}}{{bd}} < \frac{{bc}}{{bd}} \Rightarrow \frac{a}{b}.\frac{d}{d} < \frac{b}{b}.\frac{c}{d} \Rightarrow \frac{a}{b}.1 < 1.\frac{c}{d} \Rightarrow \frac{a}{b} < \frac{c}{d}

Câu 6 - SBT Toán 7 tr 6:

Chứng minh rằng:

a) Chứng tỏ rằng nếu \frac{a}{b} < \frac{c}{d} (b > 0, d > 0) thì \frac{a}{b} < \frac{{a + c}}{{b + d}} < \frac{c}{d}

b) Hãy viết ba số hữu tỉ xen giữa \frac{{ - 1}}{3} và  \frac{{ - 1}}{4}

Lời giải:

Vì \frac{a}{b} < \frac{c}{d}và b > 0, d > 0 nên \frac{{a.d}}{{b.d}} < \frac{{b.c}}{{b.d}} \Rightarrow ad < bc

\begin{array}{l} \Rightarrow ad + ab < bc + ab\\ \Leftrightarrow a\left( {b + d} \right) < b\left( {a + c} \right) \end{array}

Vì b > 0 và d > 0 nên b + d > 0

\Rightarrow \frac{a}{b} < \frac{{a + c}}{{b + d}}(1)

Lại có ad < bc \Rightarrow ad + cd < bc + cd

\Rightarrow d\left( {a + c} \right) < c\left( {b + d} \right) \Rightarrow \frac{{a + c}}{{b + d}} < \frac{c}{d}(2)

Từ (1) và (2) suy ra \frac{a}{b} < \frac{{a + c}}{{b + d}} < \frac{c}{d}

b) Vì \frac{{ - 1}}{3} < \frac{{ - 1}}{4}nên áp dùng câu a có:

\frac{{ - 1}}{3} < \frac{{\left( { - 1} \right) + \left( { - 1} \right)}}{{3 + 4}} < \frac{{ - 1}}{4} \Leftrightarrow \frac{{ - 1}}{3} < \frac{{ - 2}}{7} < \frac{{ - 1}}{4}

Lại có: \frac{{ - 1}}{3} < \frac{{ - 2}}{7} \Rightarrow \frac{{ - 1}}{3} < \frac{{\left( { - 1} \right) + \left( { - 2} \right)}}{{3 + 7}} < \frac{{ - 2}}{7} \Rightarrow \frac{{ - 1}}{3} < \frac{{ - 3}}{{10}} < \frac{{ - 2}}{7}

Và \frac{{ - 1}}{3} < \frac{{ - 3}}{{10}} \Rightarrow \frac{{ - 1}}{3} < \frac{{\left( { - 1} \right) + \left( { - 3} \right)}}{{3 + 10}} < \frac{{ - 3}}{{10}} \Rightarrow \frac{{ - 1}}{3} < \frac{{ - 4}}{{13}} < \frac{{ - 3}}{{10}}

Vậy ba số hữu tỉ xen giữa \frac{{ - 1}}{3} và \frac{{ - 1}}{4} là \frac{{ - 3}}{{10}};\frac{{ - 4}}{{13}};\frac{{ - 2}}{7}

Câu 7 - SBT Toán 7 tr 6:

Tìm x ∉Q , biết rằng x là số âm lớn nhất được viết bằng 3 chữ số 1.

Lời giải:

x là số hữu tỉ âm nên x có dạng \frac{{ - a}}{b}

Để x là số âm lớn nhất thì a < b

Mà x được viết bằng 3 chữ số 1 nên a = 1 và b = 11

Vậy số hữu tỉ x cần tìm là \frac{{ - 1}}{{11}}

Câu 8 - SBT Toán 7 tr 6:

So sánh các số hữu tỉ sau bằng cách nhanh nhất

a, \frac{{ - 1}}{5} và \frac{1}{{1000}}b, \frac{{267}}{{ - 268}}và \frac{{ - 1347}}{{1343}}
c, \frac{{ - 13}}{{38}} và \frac{{29}}{{ - 88}}d, \frac{{ - 18}}{{31}} và \frac{{ - 181818}}{{313131}}

Lời giải:

a, Có \frac{{ - 1}}{5} < 0 và \frac{1}{{1000}} > 0 nên \frac{{ - 1}}{4} < \frac{1}{{1000}}

b, Có \frac{{267}}{{ - 268}} = \frac{{ - 267}}{{268}} > \frac{{ - 268}}{{268}} = - 1

và \frac{{ - 1347}}{{1343}} < \frac{{ - 1343}}{{1343}} = - 1 nên \frac{{267}}{{ - 268}} > \frac{{ - 1347}}{{1343}}

c, Có \frac{{ - 13}}{{38}} < \frac{{ - 13}}{{39}} = \frac{{ - 1}}{3} và  \frac{{29}}{{ - 88}} = \frac{{ - 29}}{{88}} > \frac{{ - 29}}{{87}} = \frac{{ - 1}}{3}nên \frac{{ - 13}}{{38}} < \frac{{29}}{{ - 88}}

d, Có \frac{{ - 181818}}{{313131}} = \frac{{ - 181818:10101}}{{313131:10101}} = \frac{{ - 18}}{{31}}

Câu 9 - SBT Toán 7 tr 6:

Cho a, b ∉ Z, b > 0. So sánh 2 số hữu tỉ \frac{a}{b} và \frac{{a + 2001}}{{b + 2001}}

Lời giải:

Ta có: a(b+ 2001) = ab + 2001a

b(a+ 2001) = ab + 2001b

Vì b > 0 nên b + 2002 > 0

TH1: Nếu a > b thì ab + 2001a > ab + 2001b

=> a(b + 2001 ) > b( a + 2001)

\Rightarrow \frac{a}{b} > \frac{{a + 2001}}{{b + 2001}}

TH2: Nếu a < b thì ab + 2001a < ab + 2001b

=> a(b + 2001 ) < b( a + 2001)

\Rightarrow \frac{a}{b} < \frac{{a + 2001}}{{b + 2001}}

TH3: Nếu a = b thì \frac{a}{b} = \frac{{a + 2001}}{{b + 2001}}

Bài tập bổ sung:

Câu 1.1 - SBT Toán 7 tr 5:

Tập hợp các phân số bằng phân số  \frac{{ - 25}}{{35}}là:

A. \left\{ { - \frac{{25k}}{{35k}}|k \in Z,k \ne 0} \right\}B. \left\{ { - \frac{{2k}}{{3k}}|k \in Z,k \ne 0} \right\}
C. \left\{ { - \frac{{50k}}{{70k}}|k \in Z,k \ne 0} \right\}D. \left\{ { - \frac{{5k}}{{7k}}|k \in Z,k \ne 0} \right\}

Hãy chọn đáp án đúng

Lời giải:

Có \frac{{ - 25}}{{35}} = \frac{{ - 5.5}}{{7.5}} = \frac{{ - 5k}}{{7k}} với k = 5 nên đáp án đúng là đáp án D

Câu 2.2 - SBT Toán 7 tr 6:

Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng điịnh đúng:

A) \frac{{ - 25}}{{35}}1) là số hữu tỉ dương
B) \frac{{ - 25}}{{35}}2) là số hữu tỉ âm
C) \frac{{ - 25}}{{35}}3) không là số hữu tỉ dưỡng cũng không là số hữu tỉ âm
D) \frac{{ - 25}}{{35}}4) không là số hữu tỉ
5) vừa là số hữu tỉ âm vừa là số hữu tỉ dương

Lời giải:

Nối theo thứ tự: A – 3; B – 1; C – 2; D – 4

Câu 1.3 - SBT Toán 7 tr 7:

Viết dạng chung của các số hữu tỉ bằng \frac{{ - 628628}}{{942942}}

Lời giải:

Có \frac{{ - 628628}}{{942942}} = \frac{{ - 628628:1001}}{{942942:1001}} = \frac{{ - 628}}{{942}} = \frac{{ - 2}}{3}

Dạng chung của các số hữu tỉ bằng \frac{{ - 628628}}{{942942}} là \frac{{ - 2k}}{{3k}};k \in Z;k \ne 0

Câu 1.4 - SBT Toán 7 tr 7:

Cho số hữu tỉ \frac{a}{b} khác 0. Chứng minh rằng:

a, \frac{a}{b} là số hữu tỉ dương nếu a và b cùng dấu

b, \frac{a}{b} là số hữu tỉ âm nếu a và b khác dấu

Lời giải:

Xét số hữu tỉ \frac{a}{b}, giả sử b > 0

a, Nếu a, b cùng dấu thì a > 0 và b > 0

Suy ra \frac{a}{b} > \frac{0}{b} = 0 hay \frac{a}{b}dương

b, Nếu a, b khác dấu thì a < 0 và b > 0

Suy ra \frac{a}{b} < \frac{0}{b} = 0 hay \frac{a}{b}âm

Câu 1.5 - SBT Toán 7 tr 7:

So sánh \frac{a}{b}\left( {b > 0} \right) và \frac{{a + n}}{{b + n}}\left( {n \in N*} \right)

Lời giải:

Bài toán được chia thành 3 trường hợp:

Trường hợp 1: Nếu a < b thì an < bn (vì n \in N*nên n > 0)

\begin{array}{l} \Rightarrow ab + an < ab + bn\\ \Rightarrow a\left( {b + n} \right) < b\left( {a + n} \right) \end{array}

Mà b > 0 và b + n > 0 nên ta có: \frac{{a\left( {b + n} \right)}}{{b\left( {b + n} \right)}} < \frac{{b\left( {a + n} \right)}}{{b\left( {b + n} \right)}} \Rightarrow \frac{a}{b} < \frac{{a + n}}{{b + n}}

Trường hợp 2: Nếu a > b thì an > bn (vì n \in N* nên n > 0)

\begin{array}{l} \Rightarrow ab + an > ab + bn\\ \Rightarrow a\left( {b + n} \right) > b\left( {a + n} \right) \end{array}

Mà b > 0 và b + n > 0 nên ta có: \frac{{a\left( {b + n} \right)}}{{b\left( {b + n} \right)}} > \frac{{b\left( {a + n} \right)}}{{b\left( {b + n} \right)}} \Rightarrow \frac{a}{b} > \frac{{a + n}}{{b + n}}

Trường hợp 3: Nếu a = b thì a + n = b + n. Khi đó: \frac{a}{b} = \frac{{a + n}}{{b + n}} = 1

Câu 1.6 - SBT Toán 7 tr 7:

So sánh các số hữu tỉ:

a, \frac{4}{9} và \frac{{13}}{{18}}b, \frac{{ - 15}}{7}và \frac{{ - 6}}{5}
c, \frac{{278}}{{37}} và \frac{{287}}{{46}}d, \frac{{ - 157}}{{623}} và \frac{{ - 47}}{{213}}

Lời giải

Áp dụng bài 1.5 có:

a, Có \frac{4}{9} < 1 \Rightarrow \frac{4}{9} < \frac{{4 + 9}}{{9 + 9}} = \frac{{13}}{{18}}

b, Có \frac{{ - 15}}{7} < 1 \Rightarrow \frac{{ - 15}}{7} < \frac{{ - 15 + 3}}{{7 + 3}} = \frac{{ - 12}}{{10}} = \frac{{ - 6}}{5}

c, Có \frac{{278}}{{37}} > 1 \Rightarrow \frac{{278 + 9}}{{37 + 9}} = \frac{{287}}{{46}}

d, Có \frac{{ - 157}}{{623}} < 1 \Rightarrow \frac{{ - 157}}{{623}} < \frac{{ - 157 + 16}}{{623 + 16}} = \frac{{ - 141}}{{639}} = \frac{{ - 47}}{{213}}

Câu 1.7 - SBT Toán 7 tr 7:

Tìm phân số có mẫu bằng 7, lớn hơn \frac{{ - 5}}{9} và nhỏ hơn \frac{{ - 2}}{9}

Lời giải:

Gọi phân số cần tìm có dạng \frac{x}{7}\left( {x \in Z} \right) sao cho \frac{{ - 5}}{9} < \frac{x}{7} < \frac{{ - 2}}{9}

\Rightarrow \frac{{ - 35}}{{63}} < \frac{{9x}}{{63}} < \frac{{ - 14}}{{63}} \Rightarrow - 35 < 9x < - 14mà x là số nguyên nên x = -2 hoặc x = -3

Vậy các phân số cần tìm là: \frac{{ - 2}}{7};\frac{{ - 3}}{7}

Câu 1.8 - SBT Toán 7 tr 7:

Tìm phân số có tử bằng 7, lớn hơn \frac{{ - 25}}{{35}} và nhỏ hơn \frac{{ - 25}}{{35}}

Lời giải:

Gọi phân số cần tìm có dạng \frac{7}{x}\left( {x \in Z;x \ne 0} \right) sao cho \frac{{10}}{{13}} < \frac{7}{x} < \frac{{10}}{{11}}

\Rightarrow \frac{{70}}{{91}} < \frac{{70}}{{10x}} < \frac{{70}}{{77}} \Rightarrow 77 < 10x < 91mà x là số nguyên nên x = 8 hoặc x = 9

Vậy các phân số cần tìm là: \frac{7}{8};\frac{7}{9}

-----------

Để học tốt Toán 7, ngoài việc ôn tập kiến thức trong SGK môn Toán, các em học sinh cần siêng năng giải bài tập để nâng cao kỹ năng giải Toán cũng như làm quen với nhiều dạng bài tập Toán khác nhau. Chuyên mục Giải SBT Toán 7 được giới thiệu trên VnDoc bao gồm hướng dẫn giải cho các câu hỏi trong sách bài tập Toán 7, giúp các em học sinh biết cách giải các bài tập cơ bản và nâng cao Toán 7, từ đó nâng cao kỹ năng giải Toán và đạt điểm cao trong các bài kiểm tra môn Toán sắp tới.

Ngoài Giải bài tập SBT Toán 7 bài 1: Tập hợp Q các số hữu tỉ, mời các bạn tham khảo thêm: Giải bài tập Toán lớp 7, Giải Vở BT Toán 7, Đề thi học kì 1 lớp 7, Đề thi giữa kì 1 lớp 7, Đề thi học kì 2 lớp 7... được cập nhật liên tục trên VnDoc.com.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 7, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 7 sau: Nhóm Tài liệu học tập lớp 7. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Đánh giá bài viết
133 17.132
Tìm thêm: Giải bài tập SBT toán lớp 7 giải bài tập toán 7 giải bài tập SBT môn toán lớp 7
Sắp xếp theo
Xóa Đăng nhập để Gửi
    Toán 7
    Tải xuống Bản in

    Giải SBT Toán 7

    Xem thêm