Giải bài tập SBT Toán 7 bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 4: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 2: Hai tam giác bằng nhau

Giải bài tập SBT Toán 7 bài 3: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh

Giải bài tập SBT Toán 7 bài 5: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc

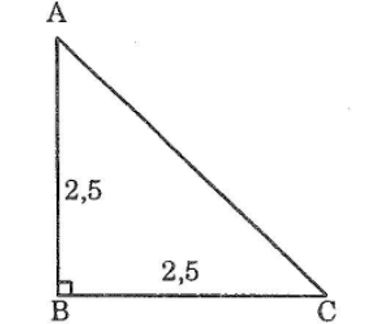
Câu 1: Vẽ tam giác ABC biết BA = Bc = 2,5 cm; ∠B =90^o. Sau đó đo các góc A và C để kiểm tra rằng ∠A =∠C =45^o

Lời giải:

Ta có: BA = BC = 2,5 cm

Suy ra : ΔABC cân tại B

Vậy: ∠A∠C =(180-∠B )/2=(180-90)/2=45^o

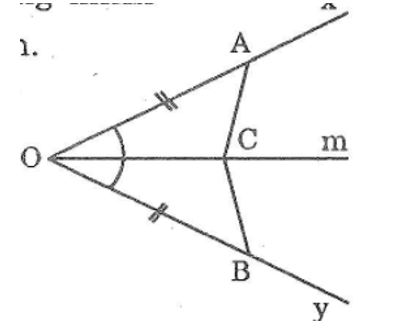
Câu 2: Dựa vào hình dưới, hãy nêu đề toán chứng minh ΔAOC=ΔBOC theo trường hợp cạnh-góc-cạnh.

Lời giải:

Cho góc nhọn xOy. Trên tia Ox lấy điểm A trên tia Oy lấy điểm B sao cho OA = OB. Lấy điểm C trên tia Om của góc xOy. Chứng minh rằng ΔAOC=ΔBOC

Câu 3: Qua trung điểm I của đoạn thẳng AB, kẻ đường vuông góc với AB, trên đường vuông góc đó lấy hai điểm C và D. nối CA, CB, DA, DB. Tìm các cặp tam giác bằng nhau trong hình vẽ.

Lời giải:

Có hai trường hợp:

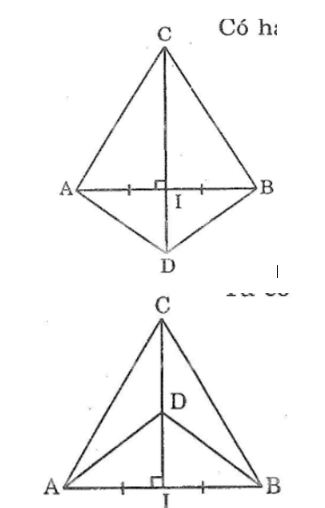
ta có: ΔAIC= ΔBIC(c.g.c)

ΔAID= ΔBID(c.g.c)

ΔACD= ΔBCD(c.c.c)

Câu 4: Vẽ ΔABC có ∠A= 90o, AB = 3cm, AC = 1cm. Sau đó đo góc C để kiểm tra rằng ∠C ̂≈72o.

Lời giải:

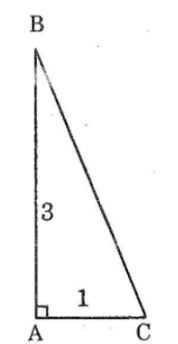
Ta có: ΔABC có ∠A =90o, AB = 3cm, AC = 1cm

Suy ra: ∠C ≈72o.

Câu 5: Qua trung điểm M của đoạn AB, kẻ đường thẳng vuông góc với AB lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB

Lời giải:

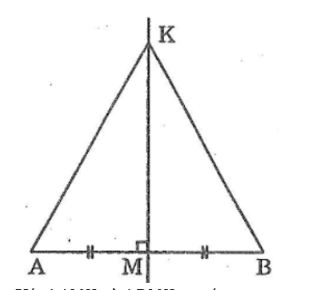
Xét ΔAMK và ΔBMK, ta có:

AM = BM (gt)

∠(AMK) =∠(BMK) =90^o (vì KM⊥AB)

Mk cạnh chung

Suy ra: ΔAMK= ΔBMK(c.g.c)

∠(AKM) = ∠ (BKM)

Vậy KM là tia phân giác của góc AKB

Câu 6: Hai đoạn thẳng AB và CD căt nhau tại trung điểm O của mối đoạn. Chứng minh rằng AC // BD

Lời giải:

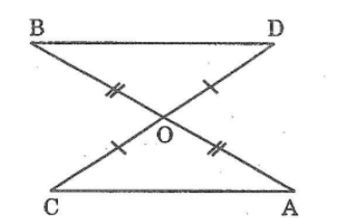
Xét Δ AOC và Δ BOD, ta có:

OA = OB (gt)

∠ (AOC) =∠ (BOD) ̂(đối đỉnh)

OC=OD

Suy ra: ΔAOC = ΔBOD (c.g.c)

∠A = ∠ B ̂(hai góc tương ứng)

Vậy: AC // BD (vì có hai góc so le trong bằng nhau)

Câu 7: Cho tam giác ABC có ∠A =90^o. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE

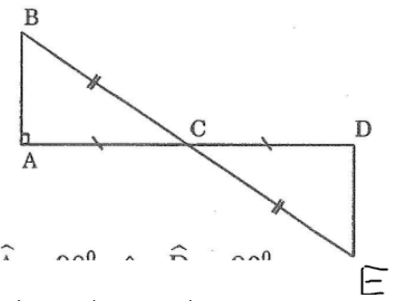
Xét ΔABC và ΔDEC, ta có:

AC = DC (gt)

∠(ACB) =∠(ECD) (đối đỉnh)

BC=EC (gt)

Suy ra: ΔABC= ΔDEC (c.g.c)

=> ∠A = ∠D ̂(hai góc tương ứng). Mà ∠A = 90^o nên ∠D =90^o

Câu 8: Cho tam giác ABC có ∠A =90^o, trên cạnh BC lấy điểm E sao cho BE = BA. Trên tia phân giác của góc B cắt AC ở D

a, So sánh các độ dài DA và DE

b, Tính số đo góc BED

Lời giải:

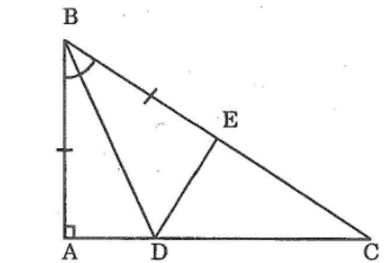
a, Xét ΔABD và ΔEBD, ta có:

AB = BE (gt)

∠(ABD) =∠ (DBE) ̂(vì Bd là tia phân giác)

BC cạnh chung

Suy ra: ΔABD và ΔEBD(c.g.c)

⇒ DA = DE (hai cạnh tương ứng)

b, Ta có: ΔABD và ΔEBD(chứng minh trên)

Suy ra: ∠A = ∠(BED) ̂(hai góc tương ứng)

Mà ∠A =90^o nên ∠(BED) =90^o