Giải bài tập SBT Toán 7 bài 4: Tính chất ba đường trung tuyến của tam giác

Bài tập môn Toán lớp 7

Giải bài tập SBT Toán 7 bài 4: Tính chất ba đường trung tuyến của tam giác được VnDoc sưu tầm và đăng tải, tổng hợp lý thuyết. Đây là lời giải hay cho các câu hỏi trong sách bài tập nằm trong chương trình giảng dạy môn Toán lớp 7. Hi vọng rằng đây sẽ là những tài liệu hữu ích trong công tác giảng dạy và học tập của quý thầy cô và các em học sinh.

Giải bài tập SBT Toán 7 bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Giải bài tập SBT Toán 7 bài 3: Quan hệ giữa ba cạnh của một tam giác - Bất đẳng thức tam giác

Giải bài tập SBT Toán 7 bài 5: Tính chất tia phân giác của một góc

Câu 1: Cho hình dưới. Điền vào chỗ trống:

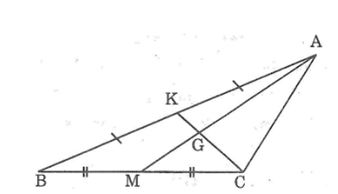
GK = … CK; AG = … GM; GK = … CG; AM = … AG; AM = … GM

Lời giải:

GK = 1/3 CK; AG = 2GM; GK = 1/2 CG; AM = 3/2 AG; AM = 3GM

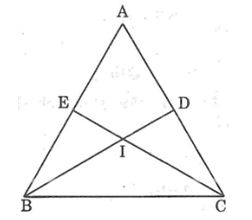
Câu 2: Chứng minh rằng nếu một tam giác có hai trung tuyến bằng nhau thì tam giác đó là tam giác cân.

Lời giải:

Giả sử ∆ABC có hai đường trung tuyến BD và CE bằng nhau.

Gọi I là giao điểm BD và CE, ta có:

BI = 2/3 BD (tính chất đường trung tuyến) (1)

CI = 2/3 CE (tính chất đường trung tuyến) (2)

Từ (1), (2) và giả thiết BD = CE suy ra: BI = CI

Suy ra: BI + ID = CI + IE ⇒ ID = IE

Xét ∆BIE và ∆CID, ta có:

BI = CI (chứng minh trên)

∠(BIE) = ∠(CID) (đối đỉnh)

IE = ID (chứng minh trên)

Suy ra: ∆BIE = ∆CID (c.g.c)

Suy ra: BE = CD (hai cạnh tương ứng) (3)

Lại có: BE = 1/2 AB (vì E là trung điểm AB) (4)

CD = 1/2 AC (vì D trung điểm AB) (5)

Từ (3), (4) và (5) suy ra: AB = CD.

Vậy tam giác ABC cân tại A.

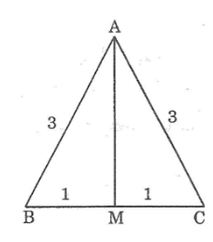
Câu 3: Tam giác ABC cân tại A có AB = CD = 34cm, BC = 32cm. Kẻ đường trung tuyến AM.

1. Chứng minh rằng AM ⊥ BC.
2. Tính độ dài AM

Lời giải:

a, Xét ΔAMB và ΔAMC, ta có:

AM = AC (gt)

BM = CM (gt)

AM cạnh chung

Suy ra: ΔAMB = ΔAMC (c.c.c)

Suy ra: ∠(AMB) = ∠(AMC) (1)

Lại có: ∠(AMB) + ∠(AMC) = 180^o (hai góc kề bù) (2)

Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90^o

Vậy AM ⊥ BC.

b, Tam giác AMB có ∠(AMB) = 90o

Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:

AB² = AM² + BM² ⇒ AM² = AB² - BM² = 34² - 16²

= 1156 - 256 = 900

Suy ra: AM = 30 (cm).

Câu 4: Gọi G là trọng tâm của tam giác ABC. Vẽ điểm D sao cho G là trung điểm của AD. Chứng minh rằng:

a, Các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b, Các đường trung tuyến của tam giá BGD bằng một nửa các cạnh của tam giác ABC.

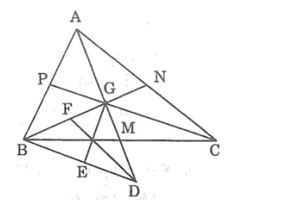
Lời giải

a, Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.

Ta có: AG = GD (gt)

AG = 2GM (tính chất đường trung tuyến)

Suy ra: GD = 2GM

Mà GD = GM + MD ⇒ GM = MD

Xét ΔBMD và ΔCMG, ta có:

BM = CM (gt)

∠(BMD) = ∠(CMG) (đối đỉnh)

MD = GM (chứng minh trên)

Suy ra: ΔBMD = ΔCMG (c.g.c)

⇒ BD = CG (hai cạnh tương ứng)

Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)

Suy ra: BD = 2/3 CP (1)

Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)

Và AG = 2/3 AM (tính chất đường trung tuyến)

Suy ra: GD = 2/3 AM (3)

Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.

b, Ta có: GM = MD (chứng minh trên)

Suy ra BM là đường trung tuyến của tam giác BGD.

Suy ra: BM = 1/2 BC (4)

Kẻ đường trung tuyến GE và DF của tam giác BGD, ta có:

FG = 1/2 BG (tính chất đường trung tuyến)

GN = 1/2 GB (tính chất đường trung tuyến)

Suy ra: FG = GN

Xét ΔDFG và ΔANG, ta có:

AG = GD (gt)

∠(DGF) = ∠(AGN) (đối đỉnh)

GF = GN (chứng minh trên)

Suy ra: ΔDFG = ΔANG (c.g.c) ⇒ DF = AN

Mà AN = 1/2 AC (gt)

Suy ra: DF = 1/2 AC (5)

Mặt khác: BD = CG (chứng minh trên)

ED = 1/2 BD (vì E là trung điểm BD)

GP = 1/2 CG (tính chất đường trung tuyến)

Suy ra: ED = GP

Lại có: ΔBMD = ΔCMG (chứng minh trên)

⇒ ∠(BDM) = ∠(CGM) hay ∠(EDG) = ∠(CGM)

(CGM) = (PGA) (đối đỉnh)

Suy ra: ∠(EDG) = ∠(PGA)

AG = GD (gt)

Suy ra: ΔPGA = ΔEDG (c.g.c) ⇒ GE = AP mà AP = 1/2 AB (gt)

Do đó: GE = 1/2 AB (6)

Từ (4), (5) và (6) suy ra các đường trung tuyến của ΔBGD bằng một nửa cạnh của ΔABC.

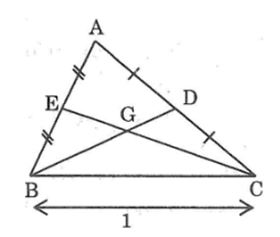
Câu 5: Tam giác ABC có BC = 10cm, các đường trung tuyến BD và CE. Chứng minh rằng BD + CE > 15cm.

Lời giải:

Gọi G là giao điểm của BD và CE.

Trong ∆GBC, ta có:

GB + GC > BC (bất đẳng thức tam giác)

GB = 2/3 BD (tính chất đường trung tuyến)

GC = 2/3 CE (tính chất đường trung tuyến)

Mà BC = 10 cm (gt)

Suy ra: 23 (BD + CE) > 10 hay BD + CE > 10 : 2/3 = 10.3/2 = 15

Vậy BD + CE > 15 (cm).

Câu 6: Cho tam giác ABC. Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = 1/2 BC. Gọi K là giao điểm của AE và CD. Chứng minh rằng DK = KC.

Lời giải:

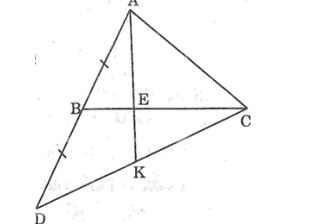
Trong ∆ACD ta có:

CB là đường trung tuyến kẻ từ đỉnh C

Mặt khác:

E ∈ BC và BE = 1/2 BC (gt)

Nên: CE = 2/3 CB

Suy ra: E là trọng tâm của ∆ACD.

Vì AK đi qua E nên AK là đường trung tuyến của ∆ACD

Suy ra K là trung điểm của CD

Vậy KD = KC.

Câu 7: Theo kết quả của bài 64 chương II, sách Bài tập toán 7 tập một ta có: Đoạn thẳng nối trung điểm hai cạnh của một tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Vận dụng kết quả trên để giải bài toán sau: Cho tam giác ABC, đường trung tuyến AD. Kẻ đường trung tuyến BE cắt AD ở G. Gọi I, K theo thứ tự là trung điểm của GA, GB. Chứng minh rằng:

a, IK // DE, IK = DE

b, AG = 2/3 AD

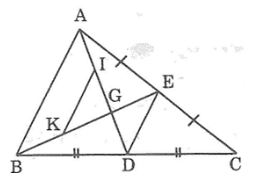
Lời giải:

a, Áp dụng kết quả bài 64 chương II sách Bài tập toán 7 vào ΔABC và ΔAGB ta có:

DE // AB và DE = 1/2 AB (1)

IK // AB và IK = 1/2 AB (2)

Từ (1) và (2) suy ra:

DE // IK và DE = IK.

b, Vì AD và BE là 2 đường trung tuyến của ΔABC cắt nhau tại G nên theo tính chất đường trung tuyến, ta có: AG = 23 AD.

Câu 8: Cho tam giác ABC vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.

a, Tính số đo góc ABD.

b, Chứng minh ΔABC = ΔBAD

c, So sánh độ dài AM và BC.

Lời giải:

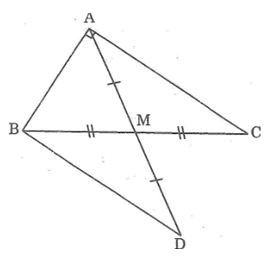
a, Xét ΔAMC và ΔBMD, ta có:

BM = MC (gt)

∠(AMB) = ∠(BMC) (đối đỉnh)

AM = MD (gt)

Suy ra: ΔAMC = ΔDMB (c.g.c)

⇒ ∠(MAC) = ∠D (2 góc tương ứng)

Suy ra: AC // BD

(vì có 2 góc ở vị trí so le trong bằng nhau)

Mà AB ⊥ AC (gt) nên AB ⊥ BD.

Vậy (ABD) = 90o.

b, Xét ΔABC và ΔBAD ta có:

AB cạnh chung

∠(BAC) = ∠(ABD) = 90o

AC = BD (vì ΔAMC = ΔDMB)

Suy ra: ΔABC = ΔBAD (c.g.c)

c, Ta có: ΔABC = ΔBAD ⇒ BC = AD (2 cạnh tương ứng)

Mặt khác: AM = 1/2 AD

Vậy AM = 1/2 BC.

Câu 9: Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Chứng minh rằng ∠(BAC) = 90^o

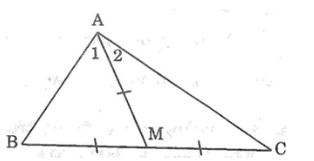
Lời giải:

Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC

Mà AM = 1/2 BC (gt) nên: AM = BM = MC.

Tam giác AMB có AM = MB nên ΔAMB cân tại M

Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)

Tam giác AMC có AM = MC nên ΔAMC cân tại M

Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)

Trong ΔABC ta có:

∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)

Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180^o ⇔ 2∠(BAC) = 180^o

Hay ∠(BAC) = 90^o.

Vậy ΔABC vuông tại A.