Đề cương ôn hè môn Toán lớp 7 năm 2024 Sách mới

Đề cương ôn hè môn Toán lớp 7 sách mới gồm các bài tập môn Đại số 7 và Hình học 7, giúp các em hệ thống lại kiến thức được học trong chương trình Toán 7 sách Chân trời sáng tạo, Kết nối tri thức, Cánh diều.

I. Đề cương ôn tập hè Toán 7 Kết nối tri thức

A. CÁC KIẾN THỨC TRỌNG TÂM

I. ĐẠI SỐ

1. Tỉ lệ thức, tính chất của dãy tỉ số bằng nhau.

2. Đại lượng tỉ lệ thuận, tính chất của các đại lượng tỉ lệ thuận, các bài toán về đại lượng tỉ lệ thuận.

3. Đại lượng tỉ lệ nghịch, tính chất của các đại lượng tỉ lệ nghịch, các bài toán về đại lượng tỉ lệ nghịch.

4. Biểu thức đại số, đa thức một biến, phép cộng và phép trừ đa thức một biến, phép nhân và phép chia đa thức một biến.

II. HÌNH HỌC

1. Tổng ba góc trong một tam giác, quan hệ giữa ba cạnh của một tam giác.

2. Hai tam giác bằng nhau, các trường hợp bằng nhau của hai tam giác, các trường hợp bằng nhau của hai tam giác vuông.

3. Tam giác cân.

4. Quan hệ giữa cạnh và góc trong nột tam giác, đường vuông góc và đường xiên.

5. Đường trung trực của một đoạn thẳng

6. Tính chất ba đường trung trực, ba đường trung tuyến, ba đường cao, ba đường phân giác của tam giác.

III. MỘT SỐ YÊU TỐ XÁC SUẤT

1. Làm quen với biến cố ngẫu nhiên.

2. Làm quen với xác suất của biến cố ngẫu nhiên.

B. BÀI TẬP 

Bài tập trắc nghiệm

Câu 1: Gieo một con xúc xắc được chế tạo cân đối. Biến cố “Số chấm xuất hiện trên con xúc xắc là 5” là biến cố:

A. Chắc chắn

B.Không thể

C. Ngẫu nhiên

D. Không chắc chắn

Câu 2: Chon ngẫu nhiên 1 số trong 4 số sau: 7; 8; 26; 101. Xác xuất để chọn được số chia hết cho 5 là:

A. 0

B.1

C. 2

D.4

Câu 3: Cho hai đa thức f(x) = 5x⁴ + x³ – x² + 1 và g(x) = –5x⁴ – x² + 2.

Tính h(x) = f(x) + g(x) và tìm bậc của h(x) . Ta được:

A. h(x)= x³– 1 và bậc của h(x) là 3

B. h(x)= x³ – 2x² +3 và bậc của h(x) là 3

C. h(x)= x⁴+3 và bậc của h(x) là 4

D. h(x)= x³ – 2x² +3 và bậc của h(x) là 5

Câu 4: Sắp xếp đa thức 6x³ + 5x⁴ – 8x⁶ – 3x² + 4 theo lũy thừa giảm dần của biến ta được:

A. 6x³+ 5x⁴ – 8x⁶ – 3x² + 4

B. –8x⁶ + 5x⁴ –3x² + 4 + 6x³

C. –8x⁶+ 5x⁴+6x³ + 4 –3x²

D. –8x⁶ + 5x⁴ +6x³ –3x² + 4

Câu 5. Biểu thức đại số biểu thị “Lập phương của hiệu của hai số x và y” là

A. x³ – y³;

B. (x – y)³;

C. x³ + y³;

D. (x + y)³.

Câu 6. Hệ số tự do của đa thức M = -8x² – 4x + 3 – 2x⁵ là

A. -2;

B. 4;

C. 3;

D. 5.

Câu 7. Cho hai đa thức P(x) = 6x³ − 3x² − 2x + 4 và G(x) = 5x² − 7x + 9. Giá trị P(x) − G(x) bằng

A. x² − 9x +13;

B. 6x³ − 8x² + 5x −5;

C. x³ − 8x² + 5x −5;

D. 5x³ − 8x² + 5x +13.

Câu 8. Trong các giá trị sau đây, đâu là nghiệm của đa thức 5x2 − 3x – 2?

A. x = 1;

B. x = - 1;

C. x = \(\frac{2}{5}\);

D. x = \(\frac{{ - 2}}{5}\).

Câu 9. Cho tam giác MNP có: \(\widehat N = 70^\circ ;\widehat P = 55^\circ\) . Khẳng định nào sau đây là đúng?

A. MP < MN;

B. MP = MN;

C. MP > MN;

D. Không đủ dữ kiện so sánh.

Câu 10. Trong các khẳng định sau, khẳng định nào sai?

A. Hình lăng trụ đứng tam giác có 4 mặt, 6 đỉnh

B. Hình lăng trụ đứng tam giác có 5 mặt, 6 đỉnh

C. Công thức tính diện tích xung quanh của hình lăng trụ đứng tứ giác và tam giác là \({S_{xq}} = C.h\)

D. Hình lăng trụ đứng tứ giác là lăng trụ đứng tứ giác có các mặt bên là các hình chữ nhật

Câu 11. Bộ ba độ dài đoạn thẳng nào sau đây không thể tạo thành một tam giác?

A. 18cm; 28cm; 10cm;

B. 5cm; 4cm; 6cm;

C. 15cm; 18cm; 20cm;

D. 11cm; 9cm; 7cm.

Bài tập tự luận

Bài 1:

a)

Tìm các tỉ số bằng nhau trong các tỉ số sau rồi lập tỉ lệ thức:

12 : 18; 0,24 : 0,32;\(\frac{4}{7}:\frac{6}{7}\)

b) Có ba bạn An, Bình, Cường cùng đi câu cá trong dịp hè. An câu được 11 con; Bình câu được 9 con; Cường câu được 12 con. Số tiền bán cá thu được tổng cộng là 192000 đồng. Hỏi nếu đem số tiền trên chia cho các bạn theo tỉ lệ với số con cá từng người câu được thì mỗi bạn nhận được bao nhiêu tiền?

Bài 2: Cho đa thức A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.

b) Tìm đa thức M(x) sao cho M(x) = A(x).B(x), biết B(x) = x – 1.

c) Tìm nghiệm của đa thức A(x).

Bài 3: Ba đội công nhân cùng chuyển một khối lượng gạch như nhau. Thời gian để đội thứ nhất, đội thứ hai và đội thứ ba làm xong công việc lần lượt là 2 giờ, 3 giờ, 4 giờ. Tính số công nhân tham gia làm việc của mỗi đội, biết rằng số công nhân của đội thứ ba ít hơn số công nhân của đội thứ hai là 5 người và năng suất lao động của các công nhân là như nhau.

Bài 4. Chọn ngẫu nhiên một số trong tập hợp M = {2; 3; 5; 6; 8; 9}.

a) Trong các biến cố sau, biến cố nào là biến cố chắc chắn? Biến cố nào là biến cố không thể và biến cố nào là biến cố ngẫu nhiên? A: “Số được chọn là số nguyên tố”; B: “Số được chọn là số có một chữ số”; C: “Số được chọn là số tròn chục”.

b) Tính xác suất của biến cố A.

Bài 5: Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3;...; 99; 100, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.

a) Viết và tính số phần tử của:

+ Tập hợp A gồm các kết quả có thể xảy ra đối với biến cổ “Số xuất hiện trên thẻ được rút ra là số có một chữ số”.

+ Tập hợp B gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 13.

+ Tập hợp C gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số nguyên tố”.

+ Tập hợp D gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 10”.

b) Tính xác suất của các biến cố trong phần a).

Bài 6: Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.

a) Chứng minh ΔABD = ΔHBD.

b) So sánh AD và DC.

c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.

Bài 7: Cho tam giác ABC cân tại A. Lấy M là trung điểm của đoạn thẳng BC.

a) Chứng minh: ΔABM = ΔACM

b) Chứng minh: AM là đường trung trực của đoạn thẳng BC.

c) Lấy N trên đường thẳng AM sao cho M nằm giữa A và N. Chứng minh: ΔNBC cân tại N.

d) Chứng minh: ΔABN = ΔACN và NA là tia phân giác của góc BNC.

Bài 8: Tìm các giá trị nguyên của n để 2n² – n + 2 chia hết cho 2n + 1.

II. Đề cương ôn tập hè Toán 7 Chân trời sáng tạo

A. GIỚI HẠN LÝ THUYẾT

I. Đại số: Hết bài: Phép cộng và phép trừ đa thức một biến

II. Hình học: Hết bài: Đường trung trực của một đoạn thẳng

B. BÀI TẬP

Bài 1. Viết ngẫu nhiên một số tự nhiên có 2 chữ số lớn hơn hoặc bằng 20. Tìm số phần tử của tập hợp M gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra, sau đó tính xác suất của mỗi biến cố sau:

a) Biến cố A: Số tự nhiên được viết ra là bội của 7.

b) Biến cố B: Số tự nhiên được viết ra có tổng hai chữ số là 11.

c) Biến cố C: Số tự nhiên được viết ra có chữ số hàng đơn vị gấp 2 lần chữ số hàng chục.

d) Biến cố D: Số tự nhiên được viết ra là số chia hết cho cả 3 và 4.

e) Biến cố E: Số tự nhiên được viết ra khi chia cho 4 dư 3; chia cho 6 dư 5 và chia cho 8 dư 7.

Bài 2. Số lượng tivi bán được của một cửa hàng trong một năm được biểu diễn bằng sơ đồ đoạn thẳng sau:

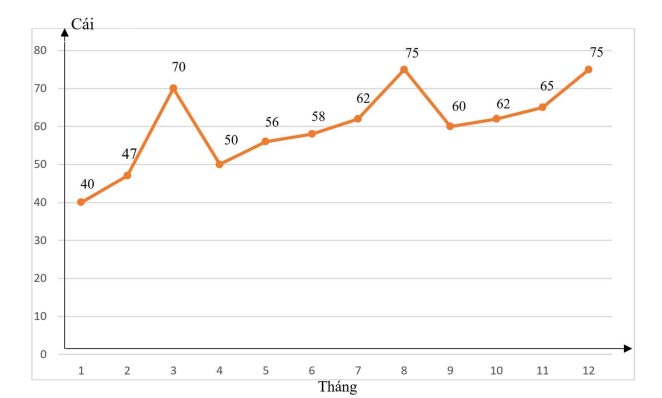
a) Lập bảng thống kê số ti vi cửa hàng bán được trong mỗi tháng của cửa hàng.

b) Số ti vi bán được trong mỗi quý chiếm bao nhiêu phần trăm so với tổng số ti vi đã bán trong cả năm (lấy một chữ số ở phần thập phân)?

Bài 3. Xếp loại học lực của 40 bạn học sinh của lớp 7A được minh họa bởi biểu đồ ở hình vẽ bên.

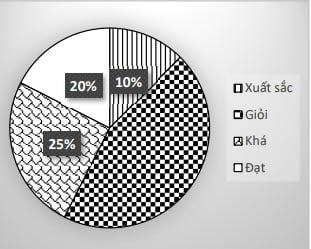
a) Kể tên các loại xếp loại học lực của lớp 7A.

b) Số phần trăm của mức xếp loại nào là chưa cho biết? Tính số phần trăm của mức xếp loại đó.

c) Tính số học sinh xếp loại Khá của lớp 7A.

Bài 4. Cho đa thức: P(x) = 7x³ + 3x⁴− x² + 5x² − 2010 − 6x³ − 2x⁴ + 2023 − x³

a) Thu gọn và sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.

b) Nêu rõ hệ số cao nhất, hệ số tự do và bậc của P(x).

c) Tính P(1) và P(-2).

d) Chứng tỏ rằng đa thức P(x) không có nghiệm

Bài 5. Cho hai đa thức: P(x) = x²+ 2x − 5 và Q(x) = x² − 9x + 5

a) Tính M(x) = P(x) + Q(x); N(x) = P(x) − Q(x)

b) Tìm nghiệm của M(x) và N(x).

Bài 6. Một người đi ô tô với vận tốc 40 km/h trong x giờ, sau đó tiếp tục đi bộ với vận tốc 5 km/h trong y giờ.

a) Hãy viết biểu thức biểu thị tổng quãng đuờng người đó đi được.

b) Tính giá trị của biểu thức trong câu a khi x=2,5 (giờ) và y=0,5 (giờ).

Bài 7. Một bác nông dân sử dụng hai chiếc máy bơm để tưới nước cho vườn cây. Máy bơm thứ nhất mỗi giờ bơm được 5m³ nước. Máy bơm thứ hai mỗi giờ bơm được 3,5m³ nước.

a) Viết biểu thức đại số biểu thị lượng nước bơm được của hai máy, nếu máy bơm thứ nhất chạy trong x giờ và máy bơm thứ hai chạy trong y giờ.

b) Sử dụng kết quả câu a, tính lượng nước bơm được của cả hai máy khi x=2 (giờ), y=3 (giờ).

c) Giả sử máy bơm thứ nhất chạy trong 2 giờ và máy bơm hai chạy trong y giờ. Tính xem máy bơm thứ hai chạy trong bao lâu khi lượng nước bơm được của hai máy là 24m³.

Bài 8. Cho tam giác ABC vuông tại A. Đường phân giác BD (DAC). Kẻ DE vuông góc với BC (E BC)

a. Chứng minh ΔABD = ΔEBD .

b. Chứng minh ΔADE cân.

c. So sánh AD và DC.

d. Kẻ đường cao AF của DABC. Chứng minh AE là tia phân giác của góc FAC.

e. Kẻ CI vuông góc với BD tại I, cắt BA kéo dài ở K. Chứng minh E, D, K thẳng hàng.

Bài 9. Cho ΔABC vuông tại A (AB < AC). Kẻ BD là phân giác của góc ABC (D thuộc AC), trên cạnh BC lấy điểm E sao cho AB = BE.

a. Chứng minh ΔABD = ΔEBD.

b. So sánh AD và DC.

c. Đường thẳng ED cắt đường thẳng AB tại F, gọi S là trung điểm của FC. Chứng minh ba điểm B, D, S thẳng hàng.

Bài 10. Cho tam giác MNP cân tại M. Lấy điểm D trên cạnh MN, điểm E trên cạnh MP sao cho ND = PE.

a) Chứng minh: ΔNDP = ΔPEN.

b) Chứng minh: ΔMDP = ΔMEN.

c) Gọi K là giao điểm của NE và DP. Chứng minh: ΔKNP cân tại K.

d) Chứng minh: MK là tia phân giác của góc NMP.

e) Lấy H là trung điểm của NP. Chứng minh: M, K, H là 3 điểm thẳng hàng.

f) Chứng minh: DE // NP