VnDoc.com

Đề cương ôn tập học kì 2 môn Toán Hình học lớp 7

203 Bài tập Hình học lớp 7

Tải về

Lớp: Lớp 7

Môn: Toán

Dạng tài liệu: Đề thi

Bộ sách: Chân trời sáng tạo

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

TUYỂN TẬP HÌNH HỌC ÔN THI HỌC KÌ 2 – TOÁN LỚP 7

Bài 1: Cho

ABC

cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho

BD CE.

Chứng minh

a) DE // BC

b)

ABE ACD  

c)

BID CIE  

(I là giao điểm của BE và CD)

d) AI là phân giác của

BAC

e)

AI BC

f) Tìm vị trí của D, E để BD = DE = EC

Bài 2: Cho

ADE

cân tại A. Trên cạnh DE lấy các điểm B và C sao cho

1

DB EC DE.

2



a)

ABC

là tam giác gì? Chứng minh

b) Kẻ

BM AD,CN AE.

Chứng minh BM = CN

c) Gọi I là giao điểm của MB và NC.

IBC

là tam giác gì? Chứng minh

d) Chứng minh AI là phân giác của

BAC

Bài 3: Cho

ABC

(AB < AC) và AM là tia phân giác của

A.

Trên AC ấy điểm D sao cho

AD AB

a) Chứng minh

BM MD

b) Gọi K là giáo điểm của AB và DM. Chứng minh

DAK BAC  

c) Chứng minh

AKC

cân

d) So sánh KM và CM

Bài 4: Cho

ABC

cân tại C. Gọi D, E lần lượt là trung điểm của các cạnh AC, BC. Các đường

thẳng AE, BD cắt nhau tại M. Các đường thẳng AM, AB cắt nhau tại I

a) Chứng minh AE = BD

b) Chứng minh DE // AB

c) Chứng minh

IM AB.

Từ đó tính IM trong trường hợp BC = 15cm, AB = 24cm

d) Chứng minh

AB 2BC CI 2AE  

Bài 5: Cho

ABC

cân tại A, đường cao AH. Gọi G là trọng tâm của

ABC

. Trên tia đối của tia

HG lấy điểm E sao cho HG = EH

a) Chứng minh BG = CG = BE = CE

b) Chứng minh

ABE ACE  

c) Chứng minh AG = GE

d) Biết AH = 9cm, BC = 8cm. Tính BE, AB

e)

ABC

thỏa mãn điều kiện gì để

GBE

là tam giác đều.

Bài 6: Cho

ABC

vuông ở C,

o

A 60 ,

tia phân giác của

BAC

cắt BC ở E, kẻ

EK AB

 

K AB

, kẻ

BD AE

 

D AE

a) Chứng minh AK = KB

b) Chứng minh AD = BC

c) Gọi I là giao điểm của BD và AC. Chứng minh IE là phân giác

BIA

d) Chứng minh BD, EK, AC đồng quy

Bài 7: Cho tam giác ABC vuông tại A. Từ 1 điểm K bất kỳ thuộc cạnh BC, vẽ KH  AC. Trên

tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng minh:

a) AB// HK.

b) Tam giác AKI cân.

c)

BAK

=

AIK

.

d)



AIC =



AKC.

Bài 8: Cho tam giác ABC cấn tại A. Gọi M là trung điểm của cạnh BC.

a) Chứng minh



ABM =



ACM.

b) Từ M vẽ MH  AB và MK  AC. Chứng minh BH = CK.

c) Từ B vẽ BP  AC, BP cắt MH tại I. Chứng minh tam giác IBM cân.

Bài 9: Cho tam giác ABC cân tại A (

A

<90

0

), vẽ BD  AC và CE  AB. Gọi H là giao điểm của

BD và CE.

a) Chứng minh:



ABD =



ACE.

b) Chứng minh



AED cân.

c) Chứng minh AH là đường trung trực của ED.

d) Trên tia đối của tia DB lấy điểm K sao cho DK = DB. Chứng minh

ECB

=

DKC

Bài 10: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA

lấy điểm E sao cho BD = CE. Vẽ DH và EK cùng vuông góc với đường thẳng BC. Chứng minh.

a) HB = CK.

b)

AHB

=

AKC

.

c) HK //DE

d)



AHE =



AKD.

e) AI  DE, I là giao điểm của DK và EH.

Bài 11: Cho góc x Oy và tia phân giác Ot. Trên tia Ot lấy điểm M bất kỳ; trên các tia Ox và Oy

lần lượt lấy các điểm A và B sao cho OA = OB; gọi H là giao điểm của AB và Ot. Chứng minh:

a) MA = MB. b) OM là đường trung trực của AB.

c) Cho biết AB = 6cm, OA = 5cm. Tính OH

Bài 12: Cho tam giác ABC vuông tại B, AM là trung tuyến. Trên tia đối của tia MA lấy điểm E

sao cho ME = AM. Chứng minh:

a)



ABM =



ECM b) AC > CE c)

BAM

=

MEC

d) BE // AC e) EC  BC

Bài 13: Cho tam giác ABC cân ở A, AB = AC = 5cm. Kẻ AH  BC (H  BC).

a) Chứng minh BH = HC và

BAH

=

CAH

.

b) Tính độ dài BH biết AH = 4cm.

c) Kẻ HD  AB (D  AB); kẻ HE  AC (E  AC); tam giác ADE là tam giác gì, vì sao?

Bài 14: Cho tam giác ABC, AB = AC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB

lấy điểm E sao cho BD = CE. Chứng minh:

a) Tam giác ADE cân b)



ABD =



ACE.

Đề cương ôn tập học kì 2 môn Toán Hình học lớp 7. Tài liệu gồm 203 câu hỏi Hình học nhằm giúp các bạn học sinh nắm chắc kiến thức được học môn Hình học 7 học kì 2. Tài liệu giúp các em học sinh ôn luyện, chuẩn bị cho kì thi cuối học kì 2 lớp 7 sắp tới đạt kết quả cao.

Những bài toán hình lớp 7 học kì 2

1. Toán 7 Chân trời sáng tạo phần Hình học
2. Các bài ôn tập hình học lớp 7 học kì 2 khác
3. Đề thi học kì 2 lớp 7 môn Toán

1. Nội dung ôn tập chung Hình học 7

Nội dung ôn tập

• Tam giác bằng nhau

• Tam giác cân. Đường trung trực của một đoạn thẳng

• Quan hệ giữa góc và cạnh đối diện trong một tam giác

• Quan hệ giữa đường vuông góc và đường xiên

• Quan hệ giữa ba cạnh của một tam giác

• Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

• Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

• Hình hộp chữ nhật, hình lập phương

• Hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác

Câu hỏi ôn tập

Câu 1: Cho $\Delta ABC$ biết rằng $\hat A = 80^\circ ;\hat C = 40^\circ ;\widehat B = 60^\circ$ . Khi đó ta có

A. $AB < AC < BC$ .

B. $AC < BC < AB$ .

C. $AB > AC > BC$ .

D. $AC > BC > AB$ .

Câu 2: Bộ ba nào sau đây có thể là độ dài ba cạnh của một tam giác?

A. 3 cm; 3 cm; 9 cm

B. 1,2 cm; 1 cm; 2,4 cm

C. 4 cm; 5 cm; 6 cm

D. 4 cm; 4 cm; 8 cm

Câu 3: Cho ΔABC có: $\widehat A = 3{5^0}$ . Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của $\widehat {ACB}$ . Số đo các góc $\widehat {ABC}; \widehat {ACB}$ là:

A. $\widehat {ABC} = 7{2^0}; \widehat {ACB} = 7{3^0}$ .

B. $\widehat {ABC} = 7{3^0}; \widehat {ACB} = 7{2^0}$ .

C. $\widehat {ABC} = 7{5^0}; \widehat {ACB} = 7{0^0}$ .

D. $\widehat {ABC} = 7{0^0}; \widehat {ACB} = 7{5^0}$ .

Câu 4: Giao điểm của ba đường trung tuyến trong một tam giác:

A. Cách đều 3 đỉnh của tam giác đó.

B. Là điểm luôn thuộc một cạnh của tam giác đó.

C. Là trọng tâm của tam giác đó.

D. Cách đều 3 cạnh của tam giác đó.

Câu 5: Độ dài hai cạnh của một tam giác là 3 cm và 11 cm. Trong các số đo sau, số đo nào sau đây là độ dài cạnh thứ 3 của tam giác:

A. 8 cm.

B. 7 cm.

C. 6 cm.

D. 9 cm.

Câu 6: Cho $\Delta ABC$ và $\Delta DEF$ có $\widehat A = \widehat D = {90^0},BC = EF,\Delta ABC = \Delta DEF$ (cạnh huyền – góc nhọn) nếu bổ sung thêm điều kiện:

A. AB = EF.

B. $\widehat B = \widehat E$ .

C. AC = DF.

D. Đáp án khác.

Câu 7: Khẳng định nào sau đây không đúng:

A. Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.

B. Trong tam giác cân hai góc ở đáy bằng nhau.

C. Tam giác có hai góc bằng nhau là tam giác đều.

D. Trong tam giác đều mỗi góc ${60^0}$ .

Câu 8: $\Delta MNP$ cân tại M. Biết góc N có số đo bằng 70^o. Số đo góc M bằng:

A. ${70^0}$ .

B. ${40^0}$ .

C. ${50^0}$ .

D. ${80^0}$ .

Câu 9: Cho $\Delta ABC$ có AM là đường phân giác đồng thời là đường cao, khi đó $\Delta ABC$ là tam giác gì?

A. Tam giác cân.

B. Tam giác vuông.

C. Tam giác đều.

D. Tam giác vuông cân.

II. Phần tự luận

Câu 10. Cho $\Delta MNP$ vuông tại M có MN < MP, kẻ đường phân giác NI của góc MNP (I thuộc MP). Kẻ IK vuông góc với NP tại K.

a) Chứng minh $\Delta IMN=\Delta IKN$

b) Chứng minh MI < IP.

c) Gọi Q là giao điểm của đường thẳng IK và đường thẳng MN, đường thẳng NI cắt QP tại D. Chứng minh $ND\bot QP$ và $\Delta QIP$ cân tại I.

Câu 11. Cho $\Delta MNP$ cân tại M $\left( {\widehat M < {{90}^0}} \right)$ . Kẻ NH ⊥ MP $\left( {H \in MP} \right)$ , PK ⊥ MN $\left( {K \in MN} \right)$ . NH và PK cắt nhau tại E.

a) Chứng minh $\Delta NHP = \Delta PKN$ .

b) Chứng minh $\Delta$ ENP cân.

c) Chứng minh ME là đường phân giác của góc NMP.

Câu 12. Cho $\Delta ABC$ cân tại A, có đường trung tuyến AM.

a) Chứng minh $\Delta ABM = \Delta ACM.$

b) Từ điểm M vẽ đường thẳng ME vuông góc với $AB{\rm{ }}\left( {E \in AB} \right)$ và vẽ đường thẳng MF vuông góc với $AC{\rm{ }}\left( {F \in AC} \right)$ . Chứng minh ME = MF.

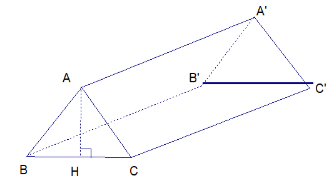
Câu 13. Một lều trại có dạng hình lăng trụ đứng đáy là tam giác, thể tích phần không gian bên trong là 2,16 cm³. Biết chiều dài CC' của lều là 2,4 m, chiều rộng BC của lều là 1,2 m. Tính chiều cao AH của lều.

Câu 14. Cho hình lăng trụ đứng có đáy là hình thoi. Biết chiều cao của hình lăng trụ 6 cm và diện tích xung quanh của hình lăng trụ là 288 cm². Tính cạnh đáy của hình lăng trụ.

2. Các bài ôn tập hình học lớp 7 học kì 2 khác

Bài 1: Cho cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho BD = CE. Chứng minh:

a) DE // BC

b) $\Delta ABE = \Delta ACD$

c) $\Delta BID = \Delta CIE$ (I là giao điểm của BE và CD)

d) AI là phân giác của

e) AI ⊥ BC

f) Tìm vị trí của D, E để BD = DE = EC

Bài 2: Cho cân tại A. Trên cạnh DE lấy các điểm B và C sao cho $DB = EC < \frac{1}{2}DE$

a) $\Delta ABC$ là tam giác gì? Chứng minh

b) Kẻ $BM \bot AD,CN \bot AE.$ Chứng minh BM = CN

c) Gọi I là giao điểm của MB và NC. $\Delta IBC$ là tam giác gì? Chứng minh.

d) Chứng minh AI là phân giác của $\widehat {BAC}$

Bài 3: Cho (AB < AC) và AM là tia phân giác của $\widehat A$ .Trên AC ấy điểm D sao cho AD = AB

a) Chứng minh BM = MD

b) Gọi K là giáo điểm của AB và DM. Chứng minh $\Delta DAK = \Delta BAC$

c) Chứng minh $\Delta AKC$ cân

d) So sánh KM và CM

Bài 4: Cho $\Delta ABC$ cân tại C. Gọi D, E lần lượt là trung điểm của các cạnh AC, BC. Các đường thẳng AE, BD cắt nhau tại M. Các đường thẳng AM, AB cắt nhau tại I

a) Chứng minh AE = BD

b) Chứng minh DE // AB

c) Chứng minh $IM \bot AB$ . Từ đó tính IM trong trường hợp BC = 15 cm, AB = 24 cm

d) Chứng minh $AB + 2BC > CI + 2AE$

Bài 5: Cho $\Delta ABC$ cân tại A, đường cao AH. Gọi G là trọng tâm của $\Delta ABC$ . Trên tia đối của tia HG lấy điểm E sao cho HG = EH

a) Chứng minh BG = CG = BE = CE

b) Chứng minh $\Delta ABE = \Delta ACE$

c) Chứng minh AG = GE

d) Biết AH = 9 cm, BC = 8 cm. Tính BE, AB

e) $\Delta ABC$ thỏa mãn điều kiện gì để $\Delta GBE$ là tam giác đều.

Bài 6: Cho $\Delta ABC$ vuông ở C, $\widehat A = {60^o}$ tia phân giác của $\widehat {BAC}$ cắt BC ở E, kẻ $EK \bot AB$ $\left( {K \in AB} \right)$ , kẻ $BD \bot AE$ $\left( {D \in AE} \right)$

a) Chứng minh AK = KB

b) Chứng minh AD = BC

c) Gọi I là giao điểm của BD và AC. Chứng minh IE là phân giác $\widehat {BIA}$

d) Chứng minh BD, EK, AC đồng quy

Bài 7: Cho tam giác ABC vuông tại A. Từ 1 điểm K bất kỳ thuộc cạnh BC, vẽ KH ⊥ AC. Trên tia đối của tia HK lấy điểm I sao cho HI = HK. Chứng minh:

a) AB // HK.

b) Tam giác AKI cân.

c) $\widehat {BAK} = \widehat {AIK}$

d) ΔAIC = ΔAKC.

Bài 8: Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh BC.

a) Chứng minh Δ ABM = Δ ACM.

b) Từ M vẽ MH ⊥ AB và MK ⊥AC. Chứng minh BH = CK.

c) Từ B vẽ BP ⊥ AC, BP cắt MH tại I. Chứng minh tam giác IBM cân.

Bài 9: Cho tam giác ABC cân tại A ( $\hat{A}$ < 90⁰), vẽ BD ⊥ AC và CE ⊥ AB. Gọi H là giao điểm của BD và CE.

a) Chứng minh: ΔABD = ΔACE.

b) Chứng minh Δ AED cân.

c) Chứng minh AH là đường trung trực của ED.

d) Trên tia đối của tia DB lấy điểm K sao cho DK = DB. Chứng minh $\widehat {ECB} = \widehat {DKC}$

Bài 10: Cho tam giác ABC cân tại A. Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Vẽ DH và EK cùng vuông góc với đường thẳng BC. Chứng minh.

a) HB = CK.

b) $\widehat {AHB} = \widehat {AKC}$

c) HK // DE

d) ΔAHE = ΔAKD.

e) AI ⊥ DE, I là giao điểm của DK và EH.

Còn tiếp. Mời bạn đọc tải tài liệu tham khảo đầy đủ!

3. Đề thi học kì 2 lớp 7 môn Toán

Đề thi học kì 2 lớp 7 môn Toán - Chân trời

Đề thi học kì 2 lớp 7 môn Toán - Kết nối

Đề thi học kì 2 lớp 7 môn Toán - Cánh diều

Tải về

Chọn file muốn tải về: