Đề cương ôn tập học kì 2 Toán 7 Cánh diều
Đề cương ôn tập Toán học kì 2 lớp 7
Đề cương ôn thi học kì 2 Toán 7 sách Cánh diều hệ thống kiến thức được học trong học kì 2 Toán 7 sách Cánh Diều, kèm các dạng bài tập trắc nghiệm và tự luận, giúp các em lên kế hoạch ôn tập, chuẩn bị cho kì thi cuối học kì 2 lớp 7 sắp tới đạt kết quả cao. Nội dung đề cương gồm:
Dạng 1: Xác suất và thống kê.
Dạng 2: Biểu thức đại số
Dạng 3: Toán lời văn
Dạng 4: Hình học
Dạng 5: Nâng cao
Dạng 1: Xác suất và thống kê.
Bài 1. Biểu đồ đoạn thẳng bên biểu diễn tổng sản phẩm quốc nội (GDP) của nước ta trong giai đoạn từ năm 2014 đến năm 2019
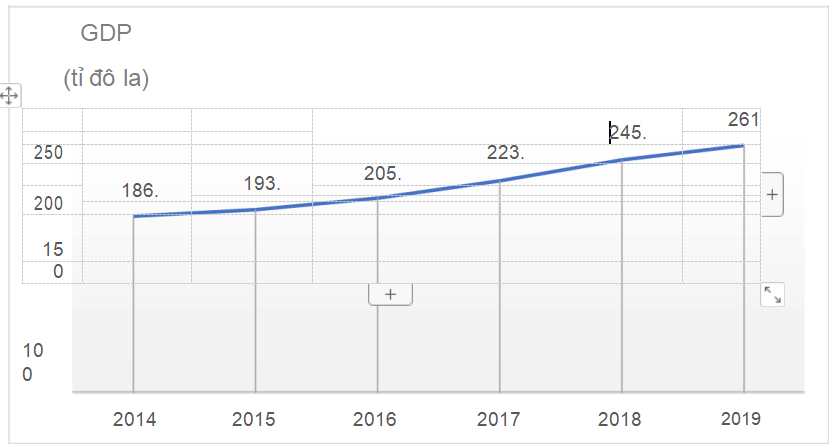
a. GDP năm 2016 là bao nhiêu?
b. GDP của nước ta có xu hướng tăng hay giảm?
c. So với năm 2014, GDP năm 2019 đã tăng bao nhiều tỉ đô la.
d. GDP năm 2017 đã tăng bao nhiêu phần trăm so với năm 2015
Bài 2. Xếp loại học lực của 40 bạn học sinh của lớp 7A được minh họa bởi biểu đồ ở hình vẽ bên.
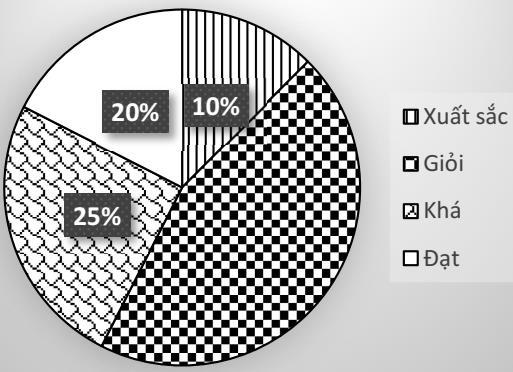
a) Kể tên các loại xếp loại học lực của lớp 7A.
b) Số phần trăm của mức xếp loại nào là chưa cho biết? Tính số phần trăm của mức xếp loại đó.
c) Tính số học sinh xếp loại Khá của lớp 7A.
Bài 3. Một hộp có 100 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3;...; 99; 100, hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
a) Viết và tính số phần tử của:
+ Tập hợp A gồm các kết quả có thể xảy ra đối với biến cổ “Số xuất hiện trên thẻ được rút ra là số có một chữ số”.
+ Tập hợp B gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số chia hết cho 13.
+ Tập hợp C gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số nguyên tố”.
+ Tập hợp D gồm các kết quả có thể xảy ra đối với biến cố “Số xuất hiện trên thẻ được rút ra là số có tổng các chữ số bằng 10”.
b) Tính xác suất của các biến cố trong phần a).
Dạng 2: Biểu thức đại số
Bài 1.
Cho hai đa thức
P(x )= 2x4 - 2x3 + 2x2 + x -1
Q (x )= -3x4 - 2x2 + 5x+ 6
a. Tính P (x ) + Q (x)
b. Tính P (x ) - Q (x)
Bài 2. Cho hai đa thức:
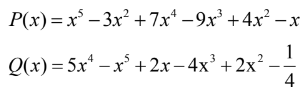
a. Tính giá trị của đa thức Q ( x) tại x =1.
b. Tìm đa thức R (x ) = P (x ) + Q (x) và K (x ) = P (x ) - Q (x) .
c. Chứng tỏ x = 0 là nghiệm của P ( x) nhưng không là nghiệm của Q (x) .
Bài 3. Cho đa thức:
![]()
a) Thu gọn và sắp xếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Chỉ ra bậc của đa thức A(x)
c) Tính A(2), A(-1)
d) Khi A(x) = 0 thì x nhận những giá trị nào?
Bài 4. Cho các đa thức:
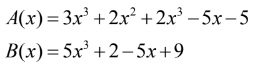
a) Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của biến x
b) Tính A(x) + B(x); A(x) – B(x)
Bài 5. Cho các đa thức:
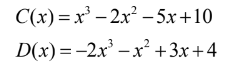
a) Tìm đa thức E(x) = C(x) + D(x)
b) Tìm đa thức F(x) = C(x) – D(x)
c) Tính E(1); F(-1).
Dạng 3: Toán lời văn
Bài 1. Một khu vườn hình chữ nhật có chiều rộng là x(m) (với x>0), chiều dài hơn chiều rộng là 5m.
a. Hãy viết biểu thức đại số biểu thị chu vi của khu vườn hình chữ nhật.
b. Hãy tính chiều dài và chiều rộng của khu vườn hình chữ nhật, biết chu vi của khu vườn là 82m.
Bài 2. Bác Hoà mua một túi rau và một số cam. Biết rằng mỗi kilôgam cam có giá 40 nghìn đổng và túi rau có giá 15 nghin đổng.
a) Hãy viết biểu thức biểu thị tổng số tiển bác Hoà phải trả nếu số cam bác Hoà mua là x kilôgam.
b) Giả sử số cam bác Hoà mua là 2,5 kilôgam. Sử dụng kết quả câu a, em hãy tính xem bác Hoà phải trả tất cả bao nhiêu tiển.
c) Giả sử Bác Hòa phải trả 135 nghìn đồng. Sử dụng kết quả của câu a, em hãy tính xem bác Hòa mua bao nhiêu kilôgam cam?
Bài 3. Một người đi ô tô với vận tốc 40 km/h trong x giờ, sau đó tiếp tục đi bộ với vận tốc 5 km/h
trong y giờ.
a) Hãy viết biểu thức biểu thị tổng quãng đuờng người đó đi được.
b) Tính giá trị của biểu thức trong câu a khi x=2,5 (giờ) và y=0,5 (giờ).
Bài 4. Một bác nông dân sử dụng hai chiếc máy bơm để tưới nước cho vườn cây. Máy bơm thứ nhất mỗi giờ bơm được 5 m3 nước. Máy bơm thứ hai mỗi giờ bơm được 3,5 m3 nước.
a) Viết biểu thức đại số biểu thị lượng nước bơm được của hai máy, nếu máy bơm thứ nhất chạy trong x giờ và máy bơm thứ hai chạy trong y giờ.
b) Sử dụng kết quả câu a, tính lượng nước bơm được của cả hai máy khi x=2 (giờ), y=3 (giờ).
c) Giả sử máy bơm thứ nhất chạy trong 2 giờ và máy bơm hai chạy trong y giờ. Tính xem máy bơm thứ hai chạy trong bao lâu khi lượng nước bơm được của hai máy là 24 m3.
Dạng 4: Hình học
Bài 1. Cho tam giác ABC vuông tại A. Đường phân giác BD (D AC). Kẻ DE vuông góc với BC (E BC)
a. Chứng minh ΔABD = ΔEBD .
b. Chứng minh ΔADE cân.
c. So sánh AD và DC.
d. Kẻ đường cao AF của DABC . Chứng minh AE là tia phân giác của góc FAC.
e. Kẻ CI vuông góc với BD tại I, cắt BA kéo dài ở K. Chứng minh E, D, K thẳng hàng.
Bài 2. Cho ΔABC vuông tại A (AB < AC). Kẻ BD là phân giác của góc ABC (D thuộc AC), trên cạnh BC lấy điểm E sao cho AB = BE.
a. Chứng minh ΔABD = ΔEBD.
b. So sánh AD và DC.
c. Đường thẳng ED cắt đường thẳng AB tại F, gọi S là trung điểm của FC. Chứng minh ba điểm B, D, S thẳng hàng.
Bài 3. Cho tam giác MNP cân tại M. Lấy điểm D trên cạnh MN, điểm E trên cạnh MP sao cho
ND = PE.
a) Chứng minh:
ΔNDP = ΔPEN.
b) Chứng minh:
ΔMDP = ΔMEN.
c) Gọi K là giao điểm của NE và DP. Chứng minh: ΔKNP cân tại K.
d) Chứng minh: MK là tia phân giác của góc NMP.
e) Lấy H là trung điểm của NP. Chứng minh: M, K, H là 3 điểm thẳng hàng.
f) Chứng minh: DE // NP
Bài 4. Cho tam giác ABC cân tại A. Lấy M là trung điểm của đoạn thẳng BC.
a) Chứng minh: ΔABM = ΔACM
b) Chứng minh: AM là đường trung trực của đoạn thẳng BC.
c) Lấy N trên đường thẳng AM sao cho M nằm giữa A và N. Chứng minh: ΔNBC cân tại N.
d) Chứng minh: ΔABN = ΔACN và NA là tia phân giác của góc BNC.
Bài 5. Cho tam giác ABC, đường trung tuyến AM. Gọi K là trung điểm của BM. Trên tia đối của tia KA lấy điểm E sao cho KE=KA.
a) Điểm M là trọng tâm của tam giác nào?
b) Gọi F là trung điểm của CE. Chứng minh rằng ba điểm A,M,F thẳng hàng
Bài 6. Cho tam giác DEF cân tại D. Lấy H là trung điểm của EF.
a) Chứng minh: ΔDEH = ΔDFH
b) Trên tia DH lấy điểm A sao cho H là trung điểm của DA. Chứng minh: DE = AF và
ΔFDA cân.
c) Gọi N là trung điểm của AF. Đoạn thẳng DN cắt đoạn thẳng EF tại G. Trên tia đối của tia NG






