Đề thi học kì 2 Toán 7 Cánh diều - Đề 2

VnDoc giới thiệu tới các bạn Đề thi học kì 2 Toán 7 sách Cánh diều năm học 2022 - 2023 - Đề 2. Đề thi Toán 7 học kì 2 bao gồm cả trắc nghiệm và tự luận cho các em tham khảo và luyện tập. Đây không chỉ là tài liệu hay cho các em ôn luyện trước kỳ thi mà còn là tài liệu cho thầy cô tham khảo ra đề.

Đề thi cuối kì 2 Toán 7 Cánh diều

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Cho các dãy dữ liệu:

(1) Tên của mỗi bạn học sinh trong lớp 7A.

(2) Số lượng học sinh của các lớp 7 đạt điểm 10 thi giữa học kì I.

(3) Số nhà của mỗi bạn học sinh lớp 7B.

(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.

Trong các dãy dữ liệu trên, dãy dữ liệu không phải là số là

A. (1);

B. (2);

C. (3);

D. (4).

Câu 2. Biểu đồ dưới đây cho biết tỉ lệ các loại kem bán được trong một ngày của một cửa hàng kem.

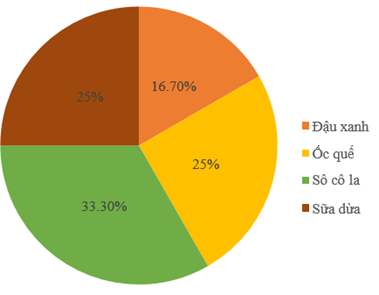
Biết rằng một ngày cửa hàng đó bán được 100 cái kem. Số lượng kem ốc quế bán được trong một ngày là bao nhiêu?

A. 20 cái;

B. 25 cái;

C. 30 cái;

D. 35 cái.

Câu 3. Tung hai con xúc xắc màu xanh và đỏ rồi quan sát số chấm xuất hiện trên mặt hai con xúc xắc. Xét biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau”. Khẳng định nào sau đây là đúng?

A. Biến cố A là biến cố không thể;

B. Biến cố A là biến cố chắc chắn;

C. Biến cố A là biến cố ngẫu nhiên;

D. Cả A, B, C đều đúng.

Câu 4. Một chiếc bình thủy tinh đựng 1 ngôi sao giấy màu tím, 1 ngôi sao giấy màu xanh, 1 ngôi sao giấy màu vàng, 1 ngôi sao giấy màu đỏ. Các ngôi sao có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 1 ngôi sao từ trong bình. Cho biến cố Y: “Lấy được 1 ngôi sao màu tím hoặc màu đỏ”. Xác suất của biến cố Y là

A. 14;

B. 12;

C. 15;

D. 1.

Câu 5. Một người đi bộ trong x (giờ) với vận tốc 4 (km/h) và sau đó đi bằng xe đạp trong y (giờ) với vận tốc 18 (km/h). Biểu thức đại số biểu thị tổng quãng đường đi được của người đó là

A. 4(x + y);

B. 22(x + y);

C. 4y + 18x;

D. 4x + 18y.

Câu 6. Giá trị của biểu thức A = –(2a + b) tại a = 1; b = 3 là

A. A = 5;

B. A = –5;

C. A = 1;

D. A = –1.

Câu 7. Hệ số tự do của đa thức 10 – 9x² – 7x⁵ + x⁶ – x⁴ là

A. –1;

B. –7;

C. 1;

D. 10.

Câu 8. Cho đa thức A(t) = 2t² – 3t + 1. Phần tử nào trong tập hợp {‒1; 0; 1; 2} là nghiệm của A(t)?

A. ‒1;

B. 0;

C. 1;

D. 2.

Câu 9. Khẳng định nào sau đây là đúng?

A. Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh nhỏ hơn;

B. Trong một tam giác, góc đối diện với cạnh nhỏ hơn là góc lớn hơn;

C. Trong một tam giác vuông, cạnh huyền là cạnh nhỏ nhất;

D. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất.

Câu 10. Cho ∆ABC có AB > BC > AC. Chọn khẳng định sai:

A. AB < BC – AC;

B. AB > BC – AC;

C. AC > AB – BC;

D. AC < AB + BC.

Câu 11. Cho tam giác ABC. Ba đường trung trực của tam giác ABC cùng đi qua một điểm M. Khẳng định nào sau đây là đúng?

A. M cách đều ba đỉnh của tam giác ABC;

B. M cách đều ba cạnh của tam giác ABC;

C. M là trọng tâm tam giác ABC;

D. M là trực tâm tam giác ABC.

Câu 12. Cho tam giác ABC có AB = AC. Trên các cạnh AB và AC lấy các điểm D,E sao cho AD = AE. Gọi K là giao điểm của BE và CD. Chọn câu sai.

A. BE = CD

B. BK = KC

C. BD = CE

D. DK = KC

II. PHẦN TỰ LUẬN (7,0 điểm)

Bài 1. (1 điểm) Tìm x biết:

a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)

b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)

Bài 2. (1,5 điểm)

Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tìm số phần tử của tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra. Sau đó, hãy tính xác suất của mỗi biến cố sau:

a) “Số tự nhiên được viết ra là bình phương của một số tự nhiên”;

b) “Số tự nhiên được viết ra là bội của 15”;

c) “Số tự nhiên được viết ra là ước của 120”.

Bài 3. (1,5 điểm) Cho đa thức A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Thu gọn, sắp xếp đa thức A(x) theo số mũ giảm dần của biến rồi tìm bậc, hệ số cao nhất của đa thức.

b) Tìm đa thức M(x) sao cho M(x) = A(x).B(x), biết B(x) = x – 1.

c) Tìm nghiệm của đa thức A(x).

Bài 4. (3 điểm)

Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC.

a) Chứng minh tam giác BEM bằng tam giác CFM

b) Chứng minh AM vuông góc với EF

c) Từ B kẻ đường thẳng vuông góc với AB tại B từ C kẻ đường vuông góc với AC tại C, 2 đường thẳng này cắt nhau tại D. Chứng minh rằng 3 điểm A, M, D thẳng hàng.

Đáp án đề kiểm tra học kì 2 Toán 7 Cánh diều

I. Trắc nghiệm:

Bảng đáp án:

II. TỰ LUẬN

Bài 1:

a) \(\dfrac{1}{{12}} + x = \dfrac{{ - 11}}{{12}}\)

\(\begin{array}{l}x = \dfrac{{ - 11}}{{12}} - \dfrac{1}{{12}}\\x = \dfrac{{ - 11 - 1}}{{12}}\\x = \dfrac{{ - 12}}{{12}} = - 1\end{array}\)

Vậy phương trình có nghiệm là x = - 1

b) \(\dfrac{{2x - 1}}{{27}} = \dfrac{3}{{2x - 1}}\)

\(\begin{array}{l}{\left( {2x - 1} \right)^2} = 27.3 = 81\\{\left( {2x - 1} \right)^2} = {\left( { \pm 9} \right)^2}\end{array}\)

Vậy phương trình có nghiệm là x = 5 hoặc x = - 4

Bài 2:

Tập hợp D gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là:

D = {10, 11, 12, …, 97, 98, 99}

Số phần tử của D là 90

a) Có sáu kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là bình phương của một số tự nhiên” là: 16, 25, 36, 49, 64, 81.

Vì thế, xác suất của biến cố trên là: \(\dfrac{6}{{90}} = \dfrac{1}{{15}}\)

b) Có sáu kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là bội của 15” là: 15, 30, 45, 60, 75, 90.

Vì thế, xác suất của biến cố trên là:\(\dfrac{6}{{90}} = \dfrac{1}{{15}}\)

c) Có tám kết quả thuận lợi cho biến cố “Số tự nhiên được viết ra là ước của 120” là: 10, 12, 15, 20, 24, 30, 40, 60.

Vì thế, xác suất của biến cố trên là: \(\dfrac{{8}}{{90}} = \dfrac{4}{45}\)

Bài 3:

a) Ta có:

A(x) = –11x⁵ + 4x – 12x² + 11x⁵ + 13x² – 7x + 2

= x² – 3x + 2.

Đa thức A(x) có bậc là 2 và hệ số cao nhất là 1.

b) M(x) = A(x).B(x)

= (x² – 3x + 2).(x – 1)

= x.(x² – 3x + 2) – 1.(x² – 3x + 2)

= x³ – 3x² + 2x – x² + 3x – 2

= x² – 4x² + 5x – 2.

c) A(x) = 0

x² – 3x + 2 = 0

x² – x – 2x + 2 = 0

x(x – 1) – 2(x – 1) = 0

(x – 1)(x – 2) = 0

x = 1 hoặc x = 2.

Vậy đa thức A(x) có nghiệm là x ∈ {1; 2}.

Bài 4:

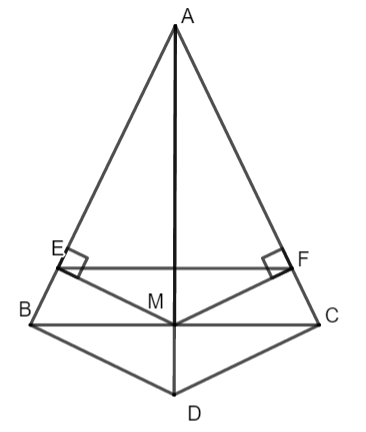
a. Xét tam giác BEM và CFM ta có:

BM = CM (vì AM là trung tuyến ứng với BC)

\(\widehat{ABC}=\widehat{ACB}\) (vì tam giác ABC cân ở A)

\(\widehat{BEM}=\widehat{ACB}={{90}^{0}}\)

\(\Rightarrow \Delta BEM=\Delta CFM\)(cạnh huyền – góc nhọn)

b. Từ câu a ta có \(\Delta BEM=\Delta CFM\Rightarrow BE=FC\)

Ta có: AE = AB – BE

Lại có: AF = AC – CF

Mà AB = AC, BE = CF

Vậy AE = AF

Trong một tam giác cân đường trung tuyến đồng thời là đường phân giác, đường trung trực, …. Nên AM là phân giác góc A _{\(\Rightarrow \widehat{BAM}=\widehat{CAM}\)}

Xét tam giác AEI và tam giác AFI ta có:

AI là cạnh chung

AE = AF

\(\widehat{BAM}=\widehat{CAM}\)

\(\Rightarrow \Delta AEM=\Delta AFM\)(c. g. c)

\(\begin{align} & \Rightarrow \widehat{AIE}=\widehat{AFM} \\ & \widehat{AIE}+\widehat{AIF}={{180}^{0}} \\ & \Rightarrow \widehat{AIE}=\widehat{AIF}={{180}^{0}}:2={{90}^{0}} \\ \end{align}\)

Vậy AM vuông góc với FE

c. Theo câu a ta có \(\Delta BEM=\Delta CFM\Rightarrow ME=MF\)

Vậy M thuộc phân giác góc A (1)

Xét tam giác vuông ABD và ACD có

AD là cạnh chung

\(\widehat{BAM}=\widehat{CAM}\)

\(\Rightarrow \Delta ABD=\Delta ACD\) (Cạnh huyền – góc nhọn)

Suy ra DB = DC nên D thuộc tia phân giác góc A (2)

Từ (1) và (2) ta có A, D, M thẳng hàng

..................................

Trên đây là Đề thi học kì 2 Toán 7 Cánh diều năm học 2022 - 2023 - Đề 2. Để chuẩn bị cho kì thi học kì 2 lớp 7 sắp tới, VnDoc giới thiệu tới các bạn chuyên mục Đề thi học kì 2 lớp 7 với đầy đủ các môn, do đội ngũ giáo viên VnDoc biên soạn hoặc sưu tầm từ nhiều trường THCS trên cả nước. Đây là tài liệu hay cho thầy cô tham khảo ra đề, cũng là nguồn tài liệu để các em học sinh ôn luyện trước kì thi. Mời thầy cô và các em tham khảo.