Bộ 23 đề thi giữa kì 1 Toán 7 năm 2024 có đáp án

VnDoc giới thiệu tới các bạn 23 Đề thi giữa kì 1 Toán 7 bộ 3 sách mới: Chân trời sáng tạo Kết nối tri thức, Cánh diều, có đầy đủ đáp án, ma trận và bản đặc tả kỹ thuật. Bộ đề thi giữa kì 1 lớp 7 môn Toán đã được phân loại rõ ràng đề thi của từng sách nên thầy cô và các bạn học sinh rất tiện lợi để theo dõi. Đây là tài liệu tham khảo hữu ích dành cho thầy cô trong quá trình ra đề thi, cũng như cho các em học sinh làm quen nhiều dạng đề kiểm tra Toán 7 khác nhau.

Lưu ý: Toàn bộ 23 đề thi và đáp án đều có trong file tải, mời thầy cô và các bạn tải về tham khảo trọn bộ tài liệu.

Link tải chi tiết từng bộ đề:

• Top 10 Đề thi giữa kì 1 Toán 7 Kết nối tri thức
• Top 6 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo
• Top 7 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án

1. Đề thi giữa kì 1 Toán 7 Kết nối tri thức

Đề số 1

Ma trận đề thi giữa học kì 1 Toán 7 KNTT

Bản đặc tả đề thi giữa kì 1 Toán 8 KNTT

Đề thi Toán giữa kì 1 lớp 7 KNTT

Phần 1. Trắc nghiệm khách quan. (3,0 điểm)

Mỗi câu sau đây đều có 4 lựa chọn, trong đó chỉ có 1 phương án đúng. Hãy khoanh tròn vào phương án đúng trong mỗi câu dưới đây:

Câu 1. [NB] Số nào đây thuộc tập hợp số hửu tỉ ?

A. √3

B. -1.4

C. π

D.1,421356237….

Câu 2. [TH] Kết quả của phép tính \((\frac{-2}{3}) ^{2}\) bằng

Câu 3. [TH] Kết quả của phép tính \(\frac{3^{7} }{3^{3} }\)bằng

Câu 4. [NB] Căn bậc hai số học của 9 là

A. 3

B. -3

C. 9

D. -9

Câu 5. [NB] Số nào là số vô tỉ trong các số sau

A. 2/3

B. √2

C. 3,5

D. 0

Câu 6. [TH] Kết quả đúng của phép chuyển vế đẳng thức: x-5 = 6 là:

A. x = - 5+6

B. X = -6+5

C. x= 6+5

D. x = -5-6

Câu 7. [NB] Giá trị tuyệt đối của số - √5

A. - √5

B. √5

C. 5

D. -5

Câu 8. [NB] Cho hình vẽ dưới đây, góc xOy đối đỉnh với góc nào?

A. góc xOy’

B. góc x’Oy’

C. góc x’Oy

D. góc xOy

Câu 9. [NB] Cho hình vẽ bên, tia phân giác của góc xOy là tia nào dưới đây?

A. Ox

B. Oy

C. Oz

D. Ot

Câu 10. [NB] Phát biểu nào sau đây diễn đạt đúng nội dung của tiên đề Euclid?

A. Có duy nhất một đường thẳng song song với một đường thẳng cho trước.

B. Điểm M nằm ngoài đường thẳng a. Đường thẳng đi qua M và song song với a là duy nhất.

C. Qua điểm M nằm ngoài đường thẳng a có ít nhất một đường thẳng song song với a

D. Qua điểm M nằm ngoài đường thẳng a có vô số đường thẳng song song với a.

Câu 11. [TH] Cho hình vẽ, khẳng định nào sau đây đúng?

A. m // n vì có hai góc trong cùng phía bù nhau

B. m // n vì có hai góc so le trong bằng nhau

C. m // n vì có hai góc đồng vị bằng nhau

D. m // n vì có hai góc đồng vị bù nhau

Câu 12. [NB] Khẳng định nào dưới đây là một định lý ?

A. Nếu nếu tổng số đo hai góc bằng 1800 thì hai góc ấy là hai góc kề bù

B. Nếu hai góc đối đỉnh thì hai góc đó bằng nhau

C. Nếu hai góc bằng nhau thì hai góc đó đối đỉnh

D. Nếu một điểm cách đều hai đầu đoạn thẳng thì điểm dó là trung điểm của đoạn thẳng ấy.

Phần 2: Tự luận (7,0 điểm)

Bài 1. a) [NB] (0.5đ) Tìm số đối của \(-\frac{2}{3}\)

b) [NB] 1.5đ) So sánh hai số: \(1\frac{1}{2}\) và \(\frac{2}{3}\)và cho biết điểm \(1\frac{1}{2}\) nằm trước hay sau điểm \(\frac{2}{3}\) trên trục số

Bài 2. Thực hiện phép tính: (1 điểm)

Bài 3. [VD] Thực hiện phép tính: (0.5 điểm)

\(0,1.\sqrt{4} + 2\sqrt{16}\)

Bài 4. [VDC] Tính giá trị biểu thức: (1 điểm)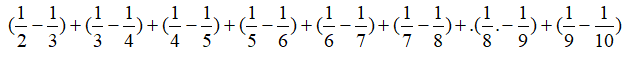

Bài 5. [TH] .(1,5 điểm)

Hình vẽ sau và cho biết hai đường thẳng a và b cùng vuông góc với đường thẳng AB và giết góc DCB bằng 600

Tính số đo góc B1

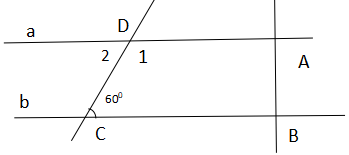
Bài 6. [VD] Vẽ hình, viết giả thiết, kết luận và chứng minh định lý “Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau”. (1 điểm)

------------- Hết -------------

Mời các bạn xem đáp án trong file tải về.

Đề số 2

Câu 1. Khẳng định nào sau đây đúng nhất:

Nếu a ∈ℤ thì

A. a ∈ ℝ;

B. a ∈ℚ;

C. Cả A và B đều đúng.

D. Cả A và B đều sai.

Câu 2: Kết quả của phép tính \(\frac{{22}}{4}:\frac{{11}}{8}\) bằng:

Câu 3: Giá trị x thỏa mãn \(\frac{3}{4}x = \frac{{15}}{{16}}\) là:

A. \(x = \frac{{ - 4}}{5}\)

B. \(x = \frac{4}{5}\)

C. \(x = \frac{{ - 5}}{4}\)

D. \(x = \frac{5}{4}\)

Câu 4: \(\frac{{ - 1}}{6}\) là kết quả của phép tính:

A. \(\frac{{22}}{{14}}.\frac{7}{{11}}.\frac{1}{6}\)	B. \(\frac{3}{4}.\left( {\frac{{ - 7}}{{14}}} \right).\frac{4}{{21}}\)
C. \(\frac{5}{{16}}.\frac{8}{{15}}.2\)	D. \(\frac{{ - 4}}{{12}}.\left( {\frac{{ - 5}}{6}} \right).\left( {\frac{{ - 9}}{{15}}} \right)\)

Câu 5. Trong các số sau đây số nào là số thập phân vô hạn không tuần hoàn:

A. 1,(3);

B. 1,2(21);

C. 1,11111…;

D. 2,64575…

Câu 6. Căn bậc hai số học của số a không âm là:

A. √ a ;

B. − √ a ;

C. √ a và − √ a

D. Không có đáp án.

Câu 7. Cho x = -12. Tính |x + 2|.

A. 10;

B. -10;

C. 12;

D. -12.

Câu 8. Khẳng định nào sau đây là đúng?

A. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm trước điểm 0, cách 0 một đoạn bằng √ 3 3 trên trục số;

B. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm sau điểm 0, cách 0 một đoạn bằng √ 3 3 trên trục số;

C. Có hai giá trị x thỏa mãn x² = 3 được biểu diễn bởi hai điểm, một điểm nằm trước và một điểm nằm sau điểm 0, hai điểm đều cách điểm 0 một khoảng bằng √ 3 3 trên trục số;

D. Không có giá trị nào của x thỏa mãn x² = 3.

Câu 9. Cho hình vẽ sau:

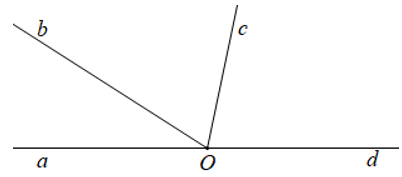
Số cặp góc kề bù (không kể góc bẹt) có trong hình vẽ trên là

A. 1;

B. 2;

C. 3;

D. 4.

Câu 10. Cho ˆ x O y = 120 ° xOy^=120° , tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

A.120°;

B. 80°;

C. 60°;

D.150°.

Câu 11. Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:

A. Hai đường thẳng đó trùng nhau;

B. Hai đường thẳng cắt nhau tại A;

C. Hai đường thẳng song song;

D. Hai đường thẳng vuông góc.

Câu 12. Định lí sau được phát biểu thành lời là:

A. Nếu một đường thẳng vuông góc một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.

C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc 60⁰.

D. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc 180⁰.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Biết biểu thức 6⁸ . 12⁵ viết được dưới dạng 2^a . 3^b. Tính a – b.

b) Cho a = \(√ 99\) = 9,94987471… và b = 5,(123).

i) Hai số b là số thập phân hữu hạn, số thập phân vô hạn tuần hoàn hay số vô tỉ? Tìm chữ số thập phân thứ năm của số b.

ii) Ước lượng tích của a và b.

Bài 2. (1,5 điểm) Thực hiện phép tính (bằng cách hợp lí nếu có thể)

\(a. 1\frac{3}{5}.\frac{4}{7}+5\frac{2}{3}.\frac{4}{7}\)	\(b. \frac{3}{8}+\left( \frac{3}{4}-1\frac{1}{5} \right):\frac{16}{5}\)
\(c. {{\left( \frac{-4}{3} \right)}^{3}}:\frac{{{\left( \frac{-1}{3} \right)}^{2}}}{6}\)

Bài 3. (1,5 điểm) Tìm x biết:

\(a. \left( x-2 \right)\left( 3-2x \right)=0\)
\(b. \frac{1}{3}+\frac{2}{3}:x=5\)

c) 7,2 : [41 – (2x – 5)] = 2³.5;

Bài 4. (2,0 điểm)

Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho \(\widehat {xOz} = 135^\circ\). Vẽ tia Ot sao cho \(\widehat {yOt} = 90^\circ\)và \(\widehat {zOt} = 135^\circ\). Gọi Ov là tia phân giác của \(\widehat {xOt}\). Các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) có phải là hai góc đối đỉnh không? Vì sao?

Bài 5. (0,5 điểm)

\(\frac{1}{2} - \frac{2}{3} + \frac{3}{4} - \frac{4}{5} + \frac{5}{6} - \frac{6}{7} + \frac{7}{8} + \frac{6}{7} - \frac{5}{6} + \frac{4}{5} - \frac{3}{4} + \frac{2}{3} - \frac{1}{2} + 1\)

Đáp án đề kiểm tra giữa kì 1 lớp 7 sách KNTT

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Ta có:

6⁸ . 12⁵ = (2 . 3)⁸ . (3. 2²)⁵ = 2⁸ . 3⁸ . 3⁵ . (2²)⁵

= 2⁸ . 2^{2 . 5} . 3^{8 + 5} = 2^{8 + 10} . 3¹³ = 2¹⁸ . 3¹³.

Khi đó a = 18 và b = 13.

Do đó a – b = 18 – 13 = 5.

Vậy a – b = 5.

b.

i) Số b = 5,(123) = 5,12312312… là số thập phân vô hạn tuần hoàn có chu kì là 123.

Chữ số thập phân thứ năm của số b là chữ số 2.

ii) Làm tròn a = √ 99 99 = 9,94987471… đến hàng đơn vị ta được a ≈ 10.

Làm tròn b = 5,12312312… đến hàng đơn vị ta được b ≈ 5.

Khi đó ước lượng tích của a và b là a . b ≈ 10 . 5 = 50.

Bài 2. (1,5 điểm)

\(a. 1\frac{3}{5}.\frac{4}{7}+5\frac{2}{3}.\frac{4}{7}=\frac{8}{5}.\frac{4}{7}+\frac{17}{3}.\frac{4}{7}=\frac{4}{7}\left( \frac{8}{5}+\frac{17}{3} \right)=\frac{4}{7}.\left( \frac{24}{15}+\frac{85}{15} \right)=\frac{4}{7}.\frac{109}{15}=\frac{436}{105}\)

\(b. \frac{3}{8}+\left( \frac{3}{4}-1\frac{1}{5} \right):\frac{16}{5}\)

\(=\frac{3}{8}+\left( \frac{3}{4}-\frac{6}{5} \right).\frac{5}{16}=\frac{3}{8}+\frac{-9}{20}.\frac{5}{16}=\frac{3}{8}-\frac{9}{64}=\frac{15}{64}\)

\(c. {{\left( \frac{-4}{3} \right)}^{3}}:\frac{{{\left( \frac{-1}{3} \right)}^{2}}}{6}=\frac{{{\left( -4 \right)}^{3}}}{{{3}^{3}}}.\frac{6}{\frac{1}{{{3}^{2}}}}=-64.6=-384\)

Bài 3. (1,5 điểm)

\(a. \left( x-2 \right)\left( 3-2x \right)=0 \Rightarrow \left[ \begin{matrix} x-2=0 \\ 3-2x=0 \\ \end{matrix} \right.\Rightarrow \left[ \begin{matrix} x=2 \\ x=-\dfrac{3}{2} \\ \end{matrix} \right.\)

Vậy \(x=2\) hoặc \(x=-\frac{3}{2}\)

\(b. \frac{1}{3}+\frac{2}{3}:x=5\)

\(\begin{align} & \frac{1}{3}+\frac{2}{3}:x=5 \\ & \Rightarrow \frac{2}{3}:x=5-\frac{1}{3}=\frac{14}{3} \\ & \Rightarrow \frac{2}{3.x}=\frac{14}{3} \\ & \Rightarrow x=\frac{1}{7} \\ \end{align}\)

Vậy \(x=\frac{1}{7}\)

c) 7,2 : [41 – (2x – 5)] = 2³ . 5.

7,2 : [41 – (2x – 5)] = 8 . 5

7,2 : [41 – (2x – 5)] = 40

41 – (2x – 5) = 7,2 : 40

41 – (2x – 5) = 0,18

2x – 5 = 41 – 0,18

2x – 5 = 40,82

2x = 40,82 + 5

2x = 45,82

x = 45,82 : 2

x = 22,91

Vậy x = 22,91.

Bài 4. (2,0 điểm)

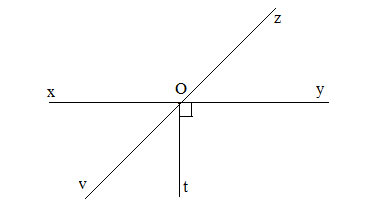
Vì \(\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot\) nên \(\widehat {xOt} = 90^\circ\)

Vì Ov là tia phân giác của \(\widehat {xOt}\) nên\(\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ\)

Vì \(\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ\)nên Ov và Oz là hai tia đối nhau

Như vậy, các góc \(\widehat {xOv}\) và \(\widehat {yOz}\) là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz

Bài 5. (0,5 điểm)

\(\frac{1}{2} - \frac{2}{3} + \frac{3}{4} - \frac{4}{5} + \frac{5}{6} - \frac{6}{7} + \frac{7}{8} + \frac{6}{7} - \frac{5}{6} + \frac{4}{5} - \frac{3}{4} + \frac{2}{3} - \frac{1}{2} + 1\)

\(= \left( {\frac{1}{2} - \frac{1}{2}} \right) + \left( { - \frac{2}{3} + \frac{2}{3}} \right) + \left( {\frac{3}{4} - \frac{3}{4}} \right) + \left( { - \frac{4}{5} + \frac{4}{5}} \right)\)

\(+ \left( {\frac{5}{6} - \frac{5}{6}} \right) + \left( { - \frac{6}{7} + \frac{6}{7}} \right) + \frac{7}{8} + 1\)

\(= 0 + \frac{7}{8} + 1 = \frac{7}{8} + \frac{8}{8} = \frac{{15}}{8}\)

2. Đề thi giữa kì 1 Toán 7 Chân trời sáng tạo

I. Trắc nghiệm khách quan: (3 điểm)

Câu 1. (NB) Trong các phân số sau, phân số nào biểu diễn số hữu tỉ \(\frac{-3}{4}\)

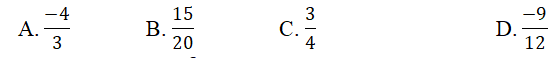
Câu 2. (NB) Số đối của \(\frac{-2}{3}\) là

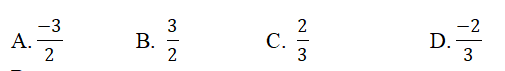
Câu 3. (NB) Chọn đáp án đúng trong các đáp án sau

A. 0,6 ∈ N

B. 0,6 ∈ Q

C. 0,6 ∈ I

D. 0,6 ∈ Z

Câu 4. (NB) Cách sắp xếp nào sau đây là đúng

Câu 5. (TH) Số \(-\frac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?

Câu 6. (TH) Kết quả củ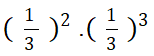a là

Câu 7. (NB) Hình hộp chữ nhật có mấy đỉnh?

A. 4 đỉnh.

B. 6 đỉnh.

C. 8 đỉnh .

D. 12 đỉnh.

Câu 8. (NB) Hình hộp chữ nhật có mấy cạnh ?

A. 12 cạnh.

B. 8 cạnh.

C.6 cạnh.

D. 4 cạnh.

Câu 9. (TH) Thể tích của hình lập phương có cạnh là 3 cm là

A. 9.

B. 12 .

C. 27.

D. 27 .

Câu 10. (NB) Hình lăng trụ đứng tam giác có số mặt bên là

A. 2 mặt.

B. 3 mặt.

C. 4 mặt.

D. 5 mặt.

Câu 11. (NB) Hình lăng trụ đứng tứ giác có số mặt đáy là.

A. 8.

B. 6.

C. 4.

D. 2.

Câu 12. (TH) Diện tích xung quanh của hình lăng trụ đứng tam giác đều có cạnh đáy là 4 cm, chiều cao 5 cm là

A. 20 cm².

B. 40 cm².

C. 60 cm².

D. 80 cm².

II. Tự luận: (7 điểm)

Câu 1. (NB) (1,0 điểm) Nêu khái niệm số hữu tỉ? Cho 2 ví dụ về số hữu tỉ?

Câu 2. (VD) (1,0 điểm) So sánh các cặp số hữu tỉ sau:

a. \(\frac{2}{3}\) và \(\frac{4}{5}\)

b - 0,6 và \(\frac{-3}{5}\)

Câu 3. (3,0 điểm) Thực hiện phép tính

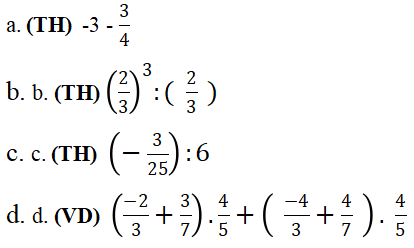
Câu 4. (TH) (1,0 điểm) Diện tích toàn phần của hình lập phương là 216 cm². Thể tích của nó là bao nhiêu ?

Câu 5. (VD) (1,0 điểm) Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính dung tích của thùng .

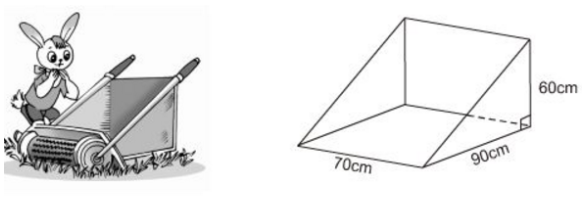
Đáp án đề kiểm tra giữa kì 1 Toán 7 CTST

I. TRẮC NGHIỆM KHÁCH QUAN (3 điểm) Mỗi câu đúng 0,25 điểm

II. Tự luận

Ma trận đề thi giữa kì 1 Toán 7

Bản đặc tả đề thi giữa kì 1 Toán 7

3. Đề thi giữa kì 1 Toán 7 Cánh diều

Đề thi giữa kì 1 Toán 7 Cánh diều Đề 1

PHẦN I. TRẮC NGHIỆM (3,0 điểm).

Chọn đáp án đúng trong các câu sau:

Câu 1. NB. Số đối của \(\frac{-2}{3}\)là

Câu 2. TH. Cách biểu diễn số trên trục số nào dưới đây đúng.

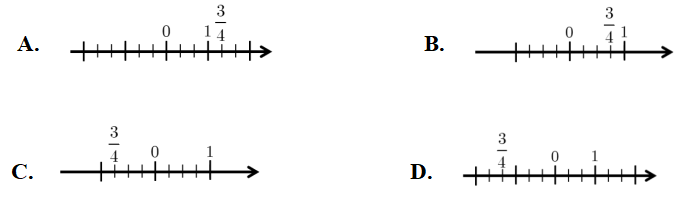
Câu 3. NB. Số đối của \(4\frac{1}{3}\); \(\sqrt{5}\); \(-\sqrt{44}\) lần lượt là

Câu 4. TH. Giá trị của biểu thức 2⁵ . \(\frac{1}{_{2}2 }\) là

A. 1.

B. 8.

C. 9²

D. 9⁴

Câu 5. NB. Trong các cách viết sau, cách viết nào biểu diển số hữu tỉ?

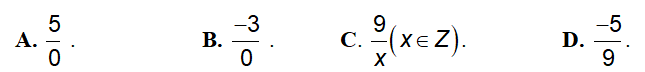
Câu 6. NB. Các mặt bên của hình lăng trụ đứng ABCD.A'B'C'D' có mặt BB'C'C là

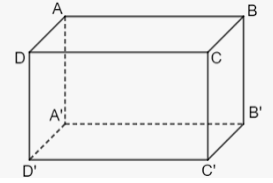
A. Các hình bình hành.

C. Các hình chữ nhật.

B. Các hình thang cân.

D. Các hình vuông.

Câu 7. NB. Hình lăng trụ đứng tam giác có số cạnh là

A. 8 .

B. 12

C. 9

D. 10

Câu 8. NB. Hình hộp chữ nhật có mặt là hình gì?

A. Hình vuông.

B. Hình chữ nhật.

C. Hình bình hành.

D. Hình thoi.

Câu 9. NB. Công thức tính diện tích xung quanh của hình hộp chữ nhật với chiều dài là, chiều rộng là, chiều cao là (cùng đơn vị đo) là:

Còn tiếp.............

Xem toàn bộ đề và đáp án trong file tải về hoặc xem tại đây: Đề kiểm tra giữa kì 1 Toán 7 Cánh diều có đáp án

Đề kiểm tra giữa kì 1 Toán 7 Cánh diều - Đề 2

I. TRẮC NGHIỆM ( 3 điểm)

Chọn chữ cái A, B, C hoặc D đứng trước câu trả lời đúng.

Câu 1: Phân số biểu diễn số hữu tỉ -0,6 là:

A. \(\dfrac{6}{{10}}\)

B. \(\dfrac{{ - 6}}{1}\)

C. \(\dfrac{{ - 12}}{{10}}\)

D. \(\dfrac{{18}}{{ - 30}}\)

Câu 2: Kết quả của phép tính: \(\left( {\dfrac{2}{3} - \dfrac{5}{4}} \right):\dfrac{{21}}{{12}}\) là:

A. 3

B. -3

C. -2

D. -4

Câu 3: Giá trị của x trong biểu thức \(- {x^3} = 27\) là:

A. \(\pm 3\)

B. \(\pm 9\)

C. 3

D. -3

Câu 4: Hình hộp chữ nhật có bao nhiêu cạnh?

A. 4

B. 6

C. 8

D. 12

Câu 5: Thể tích của hình lăng trụ đứng tứ giác có đáy là hình thoi có 2 đường chéo 8 cm, 12 cm; chiều cao 20 cm là:

A. 96cm²

B. 96ccm²

C. 192cm²

D. 192cm²

Câu 6: Để dán kín các mặt của hình lập phương cạnh 8m cần diện tích giấy là bao nhiêu ?

A. 48m²

B. 64m²

C. 512m²

D. 384m²

II. TỰ LUẬN ( 7 ĐIỂM)

Câu 7: ( 1 điểm) Thực hiện phép tính (tính nhanh nếu có thể).

a) \(\dfrac{{13}}{{25}} - \dfrac{{31}}{{41}} + \dfrac{{12}}{{25}} - \dfrac{{10}}{{41}} - 0,5\)

b) \({( - 2)^3} - {\left( { - \dfrac{1}{2}} \right)^2}:\dfrac{{ - 1}}{{16}} - {2023^0}\)

Câu 8: (1 điểm) Tìm x, biết:

a) \(\dfrac{1}{3}x - \dfrac{2}{5} = \dfrac{{ - 7}}{{15}}\) b) \({2^{x - 3}} - {3.2^x} + 92 = 0\)

Câu 9: (1 điểm)

Vào dịp Tết Nguyên đán, bà Ngọc dự định gói 20 cái bánh chưng cho gia đình. Nguyên liệu làm bánh gồm gạo nếp, đậu xanh, thịt lợn và lá dong. Mỗi cái bánh chưng sau khi gói nặng 0,75 kg gồm 0,45 kg gạo; 0,125 kg đậu xanh, 0,04 kg lá dong, còn lại là thịt. Hỏi khối lượng thịt bà cần chuẩn bị để gói bánh là khoảng bao nhiêu?

Câu 10: (3,5 điểm)

Một bể nước có dạng hình hộp chữ nhật với chiều dài 3 m. Lúc đầu bể không có nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít nước thì mực nước của bể dâng cao 0,8 m.

a) Tính chiều rộng của bể nước

b) Người ta đổ thêm 60 thùng nước thì đầy bể. Hỏi bể nước cao bao nhiêu mét?

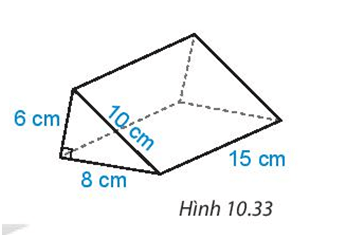
2. Tính diện tích xung quanh và thể tích hình lăng trụ đứng trong hình 10.33.

Câu 11: (0,5 điểm)

Tìm số hữu tỉ x sao cho:

\(\dfrac{{x + 1}}{{2023}} + \dfrac{{x + 2}}{{2022}} = \dfrac{{x + 3}}{{2021}} + \dfrac{{x + 4}}{{2020}}\)

Đáp án đề thi giữa kì 1 Toán 7 Cánh diều

I. TRẮC NGHIỆM ( 3 điểm)

II. TỰ LUẬN ( 7 ĐIỂM)

Câu 7: ( 1 điểm) Thực hiện phép tính (tính nhanh nếu có thể).

a)

\(\begin{array}{l}\dfrac{{13}}{{25}} - \dfrac{{31}}{{41}} + \dfrac{{12}}{{25}} - \dfrac{{10}}{{41}} - 0,5\\ = \left( {\dfrac{{13}}{{25}} + \dfrac{{12}}{{25}}} \right) + \left( { - \dfrac{{31}}{{41}} - \dfrac{{10}}{{41}}} \right) - 0,5\\ = \dfrac{{25}}{{25}} + \dfrac{{ - 41}}{{41}} - 0,5\\ = 1 + \left( { - 1} \right) - 0,5\\ = - 0,5\end{array}\)

b)

\(\begin{array}{l}{( - 2)^3} - {\left( { - \dfrac{1}{2}} \right)^2}:\dfrac{{ - 1}}{{16}} - {2023^0}\\ = \left( { - 8} \right) - \dfrac{1}{4}.\left( { - 16} \right) - 1\\ = \left( { - 8} \right) - \left( { - 4} \right) - 1\\ = \left( { - 8} \right) + 4 - 1\\ = - 5\end{array}\)

Câu 8: (1 điểm) Tìm x, biết:

a)

\(\begin{array}{l}\dfrac{1}{3}x - \dfrac{2}{5} = \dfrac{{ - 7}}{{15}}\\\dfrac{1}{3}x = \dfrac{{ - 7}}{{15}} + \dfrac{2}{5}\\\dfrac{1}{3}x = \dfrac{{ - 7}}{{15}} + \dfrac{6}{{15}}\\\dfrac{1}{3}x = \dfrac{{ - 1}}{{15}}\\x = \dfrac{{ - 1}}{{15}}:\dfrac{1}{3}\\x = \dfrac{{ - 1}}{{15}}.3\\x = \dfrac{{ - 1}}{5}\end{array}\)

Vậy \(x = \dfrac{{ - 1}}{5}\)

b)

\(\begin{array}{l}{2^{x - 3}} - {3.2^x} + 92 = 0\\{2^{x - 3}} - {3.2^3}{.2^{x - 3}} = - 92\\{2^{x - 3}} - {24.2^{x - 3}} = - 92\\{2^{x - 3}}.\left( {1 - 24} \right) = - 92\\{2^{x - 3}}.\left( { - 23} \right) = - 92\\{2^{x - 3}} = \left( { - 92} \right):\left( { - 23} \right)\\{2^{x - 3}} = 4\\{2^{x - 3}} = {2^2}\\x - 3 = 2\\x = 5\end{array}\)

Vậy x = 5

Câu 9: (1 điểm)

Khối lượng thịt trong 1 cái bánh chưng khoảng:

0,75 – (0,45 + 0,125 + 0,04) = 0,135 (kg)

Khối lượng thịt trong 20 cái bánh chưng khoảng:

0,135 . 20 = 2,7 (kg)

Vậy bà Ngọc cần chuẩn bị khoảng 2,7 kg thịt.

Câu 10: (3,5 điểm)

a) Thể tích 120 thùng nước là: 120 . 20=2400 (l) = 2,4 m3

Chiều rộng của bể nước là: 2,4 : (3.0,8) = 1 (m)

b) Thể tích 60 thùng nước là: 60 . 20 = 1200 (l) = 1,2 m3

Do người ta đổ thêm 60 thùng nước nữa thì đầy bể, nên thể tích của bể là: V = 2,4 + 1,2 = 3,6 (m3)

Chiều cao của bể là: 3,6 : (3.1) = 1,2 (m)

2.

Diện tích xung quanh hình lăng trụ đứng là :

S_xq = C_đấy . h = (6 + 10 + 8) .15 = 360 (m² )

Diện tích một đáy của hình lăng trụ là :

S _đấy = \(\frac{6 . 8}{2}\)= 24 (m² )

Thể tích của hình lăng trụ đứng là

V = S_đáy . h = 24.15 = 360 ( m³)

Câu 11: (0,5 điểm)

\(\begin{array}{l}\dfrac{{x + 1}}{{2023}} + \dfrac{{x + 2}}{{2022}} = \dfrac{{x + 3}}{{2021}} + \dfrac{{x + 4}}{{2020}}\\ \Leftrightarrow \left( {\dfrac{{x + 1}}{{2023}} + 1} \right) + \left( {\dfrac{{x + 2}}{{2022}} + 1} \right) = \left( {\dfrac{{x + 3}}{{2021}} + 1} \right) + \left( {\dfrac{{x + 4}}{{2020}} + 1} \right)\\ \Leftrightarrow \dfrac{{x + 2024}}{{2023}} + \dfrac{{x + 2024}}{{2022}} = \dfrac{{x + 2024}}{{2021}} + \dfrac{{x + 2024}}{{2020}}\\ \Leftrightarrow \dfrac{{x + 2024}}{{2023}} + \dfrac{{x + 2024}}{{2022}} - \dfrac{{x + 2024}}{{2021}} - \dfrac{{x + 2024}}{{2020}} = 0\\ \Leftrightarrow \left( {x + 2024} \right).\left( {\dfrac{1}{{2023}} + \dfrac{1}{{2022}} - \dfrac{1}{{2021}} - \dfrac{1}{{2020}}} \right) = 0\\ \Leftrightarrow \left( {x + 2024} \right) = 0\\ \Leftrightarrow x = - 2024\end{array}\)

Vậy x = -2024

4. Đề thi giữa học kì 1 lớp 7 Tải nhiều

• Bộ đề thi giữa kì 1 lớp 7 đầy đủ các môn
• Bộ đề thi giữa kì 1 Toán 7 có đáp án
• Bộ đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án
• Bộ đề thi giữa kì 1 Toán 7 Cánh diều có đáp án
• Bộ đề thi giữa học kì 1 lớp 7 môn Văn
• Bộ 7 đề thi tiếng Anh lớp 7 giữa học kì 1 có đáp án
• Bộ đề thi giữa kì 1 lớp 7 Chân trời sáng tạo - Tất cả các môn
• Đề thi giữa kì 1 lớp 7 Cánh Diều - Tất cả các môn
• Đề thi giữa kì 1 lớp 7 Kết nối tri thức - Tất cả các môn
• Bộ đề thi giữa học kì 1 lớp 7 môn Lịch sử và Địa lí
• Top 3 đề thi giữa kì 1 lớp 7 môn Lịch sử và Địa lí
• Đề thi giữa học kì 1 lớp 7 môn Tin học