Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Bộ đề thi giữa kì 1 Toán 7 có đáp án năm học 2023 - 2024 Sách mới

Chân trời sáng tạo, Kết nối tri thức, Cánh diều

29 19.065

Bài trước

Bài sau

Bộ đề kiểm tra giữa kì 1 Toán 7 năm 2022 sách mới

I. Đề thi giữa kì 1 Toán 7 Chân trời sáng tạo - Đề 1
- 1. Đề thi Toán giữa kì 1 lớp 7
- 2. Đáp án đề kiểm tra giữa kì 1 Toán 7
II. Đề thi giữa kì 1 Toán 7 Chân trời sáng tạo - Đề 2
III. Đề kiểm tra giữa kì 1 Toán 7 Kết nối tri thức với cuộc sống
IV. Đề thi giữa học kì 1 Toán 7 Cánh diều
V. Đề thi giữa học kì 1 lớp 7 Tải nhiều

Mời thầy cô và các bạn tham khảo Bộ đề thi giữa kì 1 Toán 7 năm học 2023 - 2024 (sách mới) do VnDoc đăng tải sau đây. Bộ Đề thi Toán 7 giữa học kì 1 bao gồm đề thi của 3 sách khác nhau, có đầy đủ đáp án, ma trận và bản đặc tả đề kiểm tra giữa kì 1 Toán 7. Đây không chỉ là tài liệu hay cho các em ôn luyện trước kỳ thi mà còn là tài liệu cho thầy cô tham khảo ra đề. Sau đây mời các bạn tải về tham khảo chi tiết.

I. Đề thi giữa kì 1 Toán 7 Chân trời sáng tạo - Đề 1

1. Đề thi Toán giữa kì 1 lớp 7

I. TRẮC NGHIỆM (3 điểm)

Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.

Câu 1: Số hữu tỉ là:

A. Phân số khác 0

B. Các số viết được dưới dạng $\dfrac{a}{b}\left( {a,b \in N,b \ne 0} \right)$

C. Các số viết được dưới dạng $\dfrac{a}{b}\left( {a,b \in Z,b \ne 0} \right)$

D. Các số viết được dưới dạng $\dfrac{a}{b}\left( {a,b \in Z} \right)$

Câu 2: Giá trị x thỏa mãn $27{x^2} - 3 = 0$ là:

A. $x = \dfrac{1}{9}$ ; B. $x = \dfrac{1}{3}$ ;

C. $x = 3$ D. $x = \pm \dfrac{1}{3}$ .

Câu 3: Kết quả của phép tính $\dfrac{{{3^5}{{.4}^4}}}{{{9^2}{{.8}^2}}}$ là

A. $\dfrac{3}{{16}}$ ; B. $1$ ;

C. $\dfrac{3}{4}$ ; D. Một kết quả khác.

Câu 4: Hình lăng trụ đứng tam giác có bao nhiêu mặt?

A. 3 B. 5 C. 6 D. 9

Câu 5: Hình lăng trụ đứng tam giác có đáy là tam giác có 3 cạnh đều bằng $3cm$ , chiều cao hình lăng trụ bằng $10cm$ . Diện tích xung quanh của hình lăng trụ đó là:

A. $30c{m^2}$ B. $90c{m^2}$ C. $90c{m^3}$ D. $13c{m^2}$ Câu 6: Một bể cá hình lập phương có độ dài cạnh là $0,8m$ , thể tích nước chiếm $\dfrac{3}{4}$ bể. Hỏi trong bể chứa bao nhiêu lít nước?

A. 348 lít nước B. 384 lít nước C. 405 lít nước D. 400 lít nước

II. TỰ LUẬN ( 7 ĐIỂM)

Câu 7: ( 1 điểm) Tính giá trị của các biểu thức sau:

a) ${\mkern 1mu} {\mkern 1mu} \dfrac{{ - 4}}{{13}}.10\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{{38}}{{41}}$ b) ${\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]$

Câu 8: (1,5 điểm)

Tìm x, biết:

a) $0,2 - x = - 1\dfrac{2}{5}$

b) $\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}$

c) $3.\left( { - 2x + \dfrac{5}{2}} \right).\left( {x + 11} \right) = 0$

Câu 9: (1 điểm)

Có hai tấn ảnh kích thước 20 cm x 30 cm được in trên giấy ảnh kích thước 43,2 cm x 55,8 cm. Nếu cắt ảnh theo đúng kích thước thì diện tích phần giấy ảnh còn lại là bao nhiêu?

Câu 10: (3,5 điểm)

1. Một cái thùng sắt hình hộp chữ nhật có chiều rộng bằng $\dfrac{5}{8}$ chiều dài và kém chiều dài 3,6 m; chiều cao bằng 2,5 m. Hỏi

a) Diện tích toàn phần của cái thùng

b) Nếu người ta sơn bên ngoài cái thùng, cứ 3,6 m2 tốn 3 kg sơn thì cần bao nhiêu kg sơn?

2. Người ta đào một đoạn mương có dạng hình lăng trụ đứng tứ giác. Biết mương có chiều dài 30 m, sâu 1,5 m, trên bề mặt có chiều rộng 1,8 m và đáy mương là 1,2 m.

a) Tính diện tích đáy hình thang của hình lăng trụ

b) Tính thể tích đất phải đào lên.

Câu 11: (0,5 điểm)

Cho biểu thức $A = \dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2022}}}}$ . Chứng minh $A < \dfrac{1}{4}$

2. Đáp án đề kiểm tra giữa kì 1 Toán 7

I. TRẮC NGHIỆM ( 3 điểm)

Câu 1: C

Câu 2: D

Câu 3: D

Câu 4: B

Câu 5: B

Câu 6: B

II. TỰ LUẬN ( 7 ĐIỂM)

Câu 7: ( 1 điểm)

$a)\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \dfrac{{ - 4}}{{13}}.10\dfrac{3}{{41}} - \dfrac{4}{{13}}.2\dfrac{{38}}{{41}}}\\{ = \dfrac{{ - 4}}{{13}}\left( {10\dfrac{3}{{41}} + 2\dfrac{{38}}{{41}}} \right)}\\{ = \dfrac{{ - 4}}{{13}}.13}\\{ = - 4}\end{array}b)\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} \sqrt {25} .\left( {0,4 - 1\dfrac{1}{2}} \right):\left[ {{{\left( { - 2} \right)}^3}.\dfrac{{11}}{8}} \right]}\\{ = 5.\left( {\dfrac{2}{5} - \dfrac{3}{2}} \right):\left( { - 8.\dfrac{{11}}{8}} \right)}\\{ = 5.\left( {\dfrac{4}{{10}} - \dfrac{{15}}{{10}}} \right):\left( { - 11} \right)}\\{ = 5.\dfrac{{ - 11}}{{10}}.\dfrac{{ - 1}}{{11}}}\\{ = \dfrac{1}{2}}\end{array}$

Câu 8

$\begin{array}{l}0,2 - x = - 1\dfrac{2}{5}\\ \Leftrightarrow \dfrac{2}{{10}} - x = \dfrac{{ - 7}}{5}\\ \Leftrightarrow \dfrac{1}{5} - x = \dfrac{{ - 7}}{5}\\ \Leftrightarrow x = \dfrac{1}{5} - (\dfrac{{ - 7}}{5})\\ \Leftrightarrow x = \dfrac{1}{5} + \dfrac{7}{5}\\ \Leftrightarrow x = \dfrac{8}{5}\end{array}$

Vậy $x = \dfrac{8}{5}$

$\begin{array}{l}\dfrac{{x + \dfrac{3}{2}}}{6} = \dfrac{{ - 5}}{{12}}\\ \Leftrightarrow \dfrac{{2.(x + \dfrac{3}{2})}}{{12}} = \dfrac{{ - 5}}{{12}}\\ \Leftrightarrow \dfrac{{2x + 3}}{{12}} = \dfrac{{ - 5}}{{12}}\\ \Leftrightarrow 2x + 3 = - 5\\ \Leftrightarrow 2x = - 5 - 3\\ \Leftrightarrow 2x = - 8\\ \Leftrightarrow x = - 4\end{array}$

Vậy x = -4

$\begin{array}{l}3.\left( { - 2x + \dfrac{5}{2}} \right).\left( {x + 11} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{ - 2x + \dfrac{5}{2} = 0}\\{x + 11 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \dfrac{5}{2}}\\{x = - 11}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{5}{4}}\\{x = - 11}\end{array}} \right.\end{array}$

Vậy $x \in \left\{ {\dfrac{5}{4}; - 11} \right\}$

Câu 9: (1 điểm)

Diện tích 2 tấm ảnh là: 2.(20.30)=1200 (cm2)

Diện tích tờ giấy ảnh là: 43,2 . 55,8 = 2410,56 (cm2)

Diện tích phần giấy ảnh còn lại là: 2410,56 – 1200 = 1210,56 (cm2)

Câu 10: (3,5 điểm)

a) Hiệu số phần bằng nhau là: 8 – 5 = 3 (phần)

Chiều rộng hình hộp là: 3,6 : 3 . 5 =6 (m)

Chiều dài hình hộp là: 3,6 : 3 . 8 =9,6 (m)

Diện tích xung quanh hình hộp là: ${S_{xq}} = 2.\left( {6 + 9,6} \right).2,5 = 78\left( {{m^2}} \right)$

Diện tích đáy hình hộp là: ${S_{day}} = 6.9,6 = 57,6\left( {{m^2}} \right)$

Diện tích toàn phần của thùng là: ${S_{tp}} = {S_{xq}} + 2.{S_{day}} = 78 + 2.57,6 = 193,2\left( {{m^2}} \right)$

b) Cứ 1 m2 tốn số kg sơn là: 3 : 3,6 = $\dfrac{5}{6}$ (kg)

Người ta sơn bên ngoài cái thùng cần số kg sơn là: $193,2.\dfrac{5}{6} = 161\left( {kg} \right)$

Đoạn mương có dạng hình lăng trụ tứ giác có đáy là hình thang có 2 đáy là 1,2 m và 1,8 m, chiều cao là 1,5 m; chiều cao lăng trụ là 30 m.

a) Diện tích đáy hình thang của lăng trụ là: S = (1,2+1,8).1,5:2=2,25 (m2)

b) Thể tích đất phải đào lên là: V = S . h = 2,25 . 30 = 67,5 (m2)

Câu 11: (0,5 điểm)

$\begin{array}{l}A = \dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2022}}}}\\ \Rightarrow 5A = \dfrac{5}{5} + \dfrac{5}{{{5^2}}} + \dfrac{5}{{{5^3}}} + .... + \dfrac{5}{{{5^{2022}}}}\\ = 1 + \dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2021}}}}\\ \Rightarrow 5A - A = 1 + \dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2021}}}} - \left( {\dfrac{1}{5} + \dfrac{1}{{{5^2}}} + \dfrac{1}{{{5^3}}} + .... + \dfrac{1}{{{5^{2022}}}}} \right)\\ \Rightarrow 4A = 1 - \dfrac{1}{{{5^{2022}}}}\\ \Rightarrow A = \dfrac{1}{4} - \dfrac{1}{{{{4.5}^{2022}}}} < \dfrac{1}{4}\end{array}$

Vậy $A < \dfrac{1}{4}$

II. Đề thi giữa kì 1 Toán 7 Chân trời sáng tạo - Đề 2

1. Ma trận đề kiểm tra giữa kì 1 Toán 7 CTST

TT	Chủ đề	Nội dung/Đơn vị kiến thức	Mức độ đánh giá								Tổng % điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TNKQ	TL	TNKQ	TL	TNKQ	TL	TNKQ	TL
1	Số hữu tỉ	Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ	3 câu (TN1; TN2; TN3) 0,75đ		1 câu (TN4) 0,25đ						5,0
1	Số hữu tỉ	Các phép tính với số hữu tỉ	1 câu (TN5) 0,25đ		1 câu (TN6) 0,25đ	2 câu (TL1a, TL2a) 1,0đ		4 câu (TL1b, TL1c; TL2b, TL2c) 2,0đ		1 câu (TL6) 0,5đ	5,0
2	Các hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương	2 câu (TN7, TN8) 0,5đ		1 câu (TN9) 0,25 đ			2 câu (TL3; 4) 2,25đ			3,5
2	Các hình khối trong thực tiễn	Lăng trụ đứngtam giác, lăng trụ đứng tứ giác	2 câu (TN10, TN11) 0,5 đ					2 câu (TL3; 4) 2,25đ			3,5
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	1 câu (TN12) 0,25 đ	1 (TL5a) 0,5đ				1 câu (TL5b) 0,75đ			1,5
Tổng: Số câu Điểm			9 2,25đ	1 0,5đ	3 0,75 đ	2 1,0đ		7 5,0đ		1 0,5đ	10,0
Tỉ lệ %			27,5%		17,5%		50%		5%		100%
Tỉ lệ chung			45%				55%				100%

Chú ý: Tổng tiết : 33 tiết

2. Bản đặc tả đề kiểm tra giữa học kì 1 Toán 7 CTST

TT	Chương/Chủ đề		Mức độ đánh giá	Số câu hỏi theo mức độ nhận thức
TT	Chương/Chủ đề		Mức độ đánh giá	Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
1	Số hữu tỉ	Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ	Nhận biết: – Nhận biết được số hữu tỉ và tập hợp các số hữu tỉ. – Nhận biết được số đối của một số hữu tỉ. – Nhận biết được thứ tự trong tập hợp các số hữu tỉ.	3 câu (TN1; TN2; TN3)
			Thông hiểu: – Biểu diễn được số hữu tỉ trên trục số.		1 câu (TN4)
			Vận dụng: – So sánh được hai số hữu tỉ.
		Các phép tính với số hữu tỉ	*Thông hiểu:* – Mô tả được phép tính luỹ thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai luỹ thừa cùng cơ số, luỹ thừa của luỹ thừa). – Mô tả được thứ tự thực hiện các phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ.	1TN (TN5)	1TN và 2TL (TN6, TL1a, TL2a)
		Các phép tính với số hữu tỉ	Vận dụng: – Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. – Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). – Giải quyết được một số́vấn đề thực tiễn gắn với các phép tính về số hữu tỉ. (ví dụ: các bài toán liên quan đến chuyển động trong Vật lí, trong đo đạc,...).			5TL (TL1b, TL1c; TL2b, TL2c; TL6)
2	Các hình khối trong thực tiễn	Hình hộp chữ nhật và hình lập phương	*Nhận biết:* – Nhận biết được hình hộp chữ nhật, một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương.	2TN (TN7, TN8)
			*Thông hiểu* Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, đường chéo) của hình hộp chữ nhật và hình lập phương.		1TN (TN9)
			*Vận dụng* – Giải quyết được một số vấn đề thực tiễn gắn với việc tính thể tích, diện tích xung quanh của hình hộp chữ nhật, hình lập phương.
		Lăng trụ đứngtam giác, lăng trụ đứng tứ giác	*Nhận biết* – Nhận biết được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân.	2TN (TN10, TN11)
			Thông hiểu: – Mô tả được một số yếu tố cơ bản (cạnh, góc, đường chéo) của hình chữ nhật, hình thoi, hình bình hành, hình thang cân.
			Vận dụng: – Giải quyết được một số vấn đề thực tiễn (đơn giản) gắn với việc tính chu vi và diện tích của các hình đặc biệt nói trên.			2TL (TL3; 4)
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	Nhận biết: – Nhận biết được các góc ở vị trí đặc biệt (hai góc kề bù, hai góc đối đỉnh). – Nhận biết được tia phân giác của một góc.	1TN (TN12)
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	*Vận dụng:* – Vận dụng được tính chất của các góc ở vị trí đặc biệt, tia phân giác để tính số đo góc.			1TL (TL5)

3. Đề thi giữa học kì 1 lớp 7 môn Toán sách Chân trời sáng tạo

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Hãy khoanh tròn vào phương án đúng duy nhất trong mỗi câu dưới đây:

Câu 1. Trong các câu sau, câu nào đúng?

A. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương;

B. Số 0 là số hữu tỉ dương;

C.Số nguyên âm không phải là số hữu tỉ âm;

D. Tập hợp ℚ gồm các số hữu tỉ dương và các số hữu tỉ âm.

Câu 2: Kết quả của phép tính $\frac{4}{5} - \frac{{23}}{{15}}$ bằng:

A. $\frac{7}{{15}}$

B. $\frac{{ - 1}}{{15}}$

C. $\frac{{ - 11}}{{15}}$

D. $\frac{{ - 7}}{{15}}$

Câu 3: Giá trị x thỏa mãn $x - \left( { - \frac{4}{5}} \right) = \frac{6}{{20}}$ là:

A. $x = \frac{1}{5}$

B. $x = \frac{1}{2}$

C. $x = \frac{{ - 1}}{2}$

D. $x = \frac{{ - 1}}{5}$

Câu 4: Cho x₁ là giá trị thỏa mãn $\frac{3}{7} + \frac{1}{7}:x = \frac{3}{{14}}$ và x₂ là giá trị thỏa mãn $\frac{5}{7} + \frac{6}{{11}}:x = 2$ . Hãy chọn câu trả lời đúng nhất.

A. ${x_1} = {x_2}$	B. ${x_1} < {x_2}$
C. ${x_1} > {x_2}$	D. ${x_1} = 2{x_2}$

Câu 5: Tìm số nguyên dương n thỏa mãn ${\left( {\frac{5}{3}} \right)^n} = \frac{{625}}{{81}}$

A. n = 2	B. n = 3
C. n = 4	D. n = 5

Câu 6. $\frac{1}{4}$ là kết quả của phép tính:

A. $\frac{5}{{16}} + \frac{7}{8} + \frac{{30}}{{32}}$

B. $\frac{7}{8} - \frac{{30}}{{32}}$

C. $\frac{5}{{16}} + \frac{7}{8}$

D. $\frac{5}{{16}} + \frac{7}{8} - \frac{{30}}{{32}}$

Câu 7. Trong hình dưới đây có bao nhiêu hình lập phương, bao nhiêu hình hộp chữ nhật?

Đề thi Giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án (4 đề + ma trận) (ảnh 2)

A. 2 hình lập phương, 3 hình hộp chữ nhật;

B. 1 hình lập phương, 3 hình hộp chữ nhật;

C. 2 hình lập phương, 2 hình hộp chữ nhật;

D. 0 hình lập phương, 4 hình hộp chữ nhật.

Câu 8 . Hãy chọn khẳng định sai.

Hình lập phương ABCD.A ' B ' C ' D ' có:

A. 8 đỉnh;

B. 4 mặt bên;

C. 6 cạnh;

D. 6 mặt.

Câu 9. Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,

AE = 4 cm. Khẳng định đúng là:

A. HG = 4 cm, HE = 2 cm, GC = 4 cm;

B. HG = 2 cm, HE = 2 cm, GC = 4 cm;

C. HG = 4 cm, HE = 2 cm, GC = 2 cm;

D. HG = 4 cm, HE = 4 cm, GC = 4 cm.

Câu 10. Chọn khẳng định đúng trong các khẳng định sau:

A. Hình lăng trụ đứng tam giác có mặt bên là hình tam giác;

B. Hình lăng trụ đứng tam giác là có mặt đáy là hình chữ nhật;

C. Hình lăng trụ đứng tam giác có mặt đáy là hình tam giác;

D. Hình lăng trụ đứng tam giác có mặt đáy là hình tứ giác.

Câu 11. Tấm bìa bên dưới có thể tạo lập thành một hình lăng trụ đứng có đáy là tam giác đều.

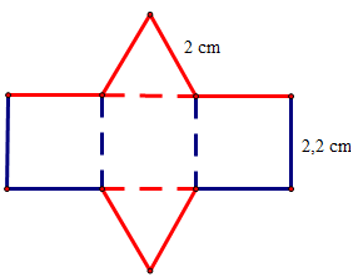
Đề thi Giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án (4 đề + ma trận) (ảnh 3)

Chiều cao của hình lăng trụ đứng là:

A. 2 cm;

B. 2,2 cm;

C. 4 cm;

D. 4,4 cm.

Câu 12. Chọn phát biểu sai:

A. Hai góc đối đỉnh thì bằng nhau;

B. Hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia được gọi là hai góc đối đỉnh;

C. Hai đường thẳng cắt nhau tại một điểm tạo thành hai cặp góc đối đỉnh;

D. Hai góc bằng nhau thì đối đỉnh.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm) Thực hiện phép tính:

$a. {{\left( \frac{-1}{2} \right)}^{2}}+\frac{3}{4}:\frac{-2}{3}$
$b. \left( 2\frac{1}{3}+\frac{1}{6} \right):\left( -3\frac{2}{3}+4\frac{1}{2} \right)$
$c. \left( -0,5-\frac{3}{5} \right):3+\frac{1}{3}+\frac{1}{6}:2$
Bài 2. (1,5 điểm) Tìm x, biết:

$a. 2x+\frac{1}{3}=\frac{5}{6}$

$b. 1\frac{2}{3}:x+\frac{3}{7}=-\frac{6}{5}$

c) (x – 5)² = (1 – 3x)².

Bài 3. (0,75 điểm) Bác Long có một căn phòng hình hộp chữ nhật có một cửa ra vào và một cửa sổ hình vuông với các kích thước như hình vẽ.

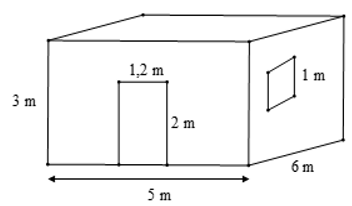
Đề thi Giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án (4 đề + ma trận) (ảnh 4)

Hỏi bác Long cần trả bao nhiêu chi phí để sơn bốn bức tường xung quanh của căn phòng này (không sơn cửa)? Biết rằng để sơn mỗi mét vuông tốn 30 nghìn đồng.

Bài 4. (1,5 điểm) Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ).

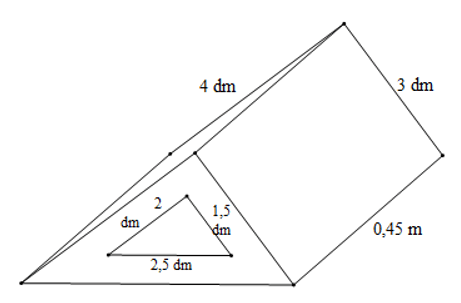
Đề thi Giữa kì 1 Toán lớp 7 Chân trời sáng tạo có đáp án (4 đề + ma trận) (ảnh 5)

a) Tính thể tích của khối gỗ.

b) Người ta muốn sơn tất cả các bề mặt của khối gỗ. Tính diện tích cần sơn (đơn vị mét vuông).

Bài 5 (1,25 điểm)

Vẽ góc xOy có số đo bằng 60⁰. Vẽ tia Om là tia đối của tia Ox.

a) Gọi tên hai góc kề bù có trong hình vừa vẽ.

b) Tính số đo góc yOm.

c) Vẽ tia Ot là tia phân giác của góc xOy. Tính số đo các góc tOy và tOm.

Bài 6 (0,5 điểm) Một công ty phát triển kĩ thuật có một số thông báo rất hấp dẫn: Cần thuê một nhóm kĩ thuật viên hoàn thành một dự án trong vòng 17 ngày, công việc rất khó khăn nhưng tiền công cho dự án rất thú vị. Nhóm kĩ thuật viên được nhận làm dự án sẽ lựa chọn một trong hai phương án trả tiền công như sau:

– Phương án 1: Nhận một lần và nhận tiền công trước với mức tiền 170 triệu đồng;

– Phương án 2: Ngày đầu tiên nhận 3 đồng, ngày sau nhận gấp 3 lần ngày trước đó.

Em hãy giúp nhóm kỹ thuật viên lựa chọn phương án để nhận được nhiều tiền công hơn và giải thích tại sao chọn phương án đó.

4. Đáp án đề kiểm tra giữa kì 1 Toán 7 CTST

Bảng đáp án trắc nghiệm

1. A	2. C	3. C	4. B	5. C	6. D
7. D	8. C	9. A	10. C	11. B	12. D

Hướng dẫn giải chi tiết tự luận

Bài 1. (1,5 điểm)

$a,{{\left( \frac{-1}{2} \right)}^{2}}+\frac{3}{4}:\frac{-2}{3}=\frac{1}{4}+\frac{3}{4}.\frac{3}{-2}=\frac{1}{4}-\frac{9}{8}=\frac{2}{8}-\frac{9}{8}=\frac{-7}{8}$

$\begin{align} & b,\left( 2\frac{1}{3}+\frac{1}{6} \right):\left( -3\frac{2}{3}+4\frac{1}{2} \right)=\left( \frac{7}{3}+\frac{1}{6} \right):\left( \frac{-7}{3}+\frac{9}{2} \right) \\ & =\left( \frac{14}{6}+\frac{1}{6} \right):\left( \frac{-14}{6}+\frac{27}{6} \right)=\frac{15}{6}:\frac{13}{6}=\frac{15}{6}.\frac{6}{13}=\frac{15}{13} \\ \end{align}$

$\begin{align} & c,\left( -0,5-\frac{3}{5} \right):3+\frac{1}{3}+\frac{1}{6}:2=\left( -\frac{1}{2}-\frac{3}{5} \right):3+\frac{1}{3}+\frac{1}{12}=-\frac{11}{10}:3+\frac{5}{12} \\ & =\frac{-11}{30}+\frac{5}{12}=\frac{-22}{60}+\frac{25}{60}=\frac{3}{60}=\frac{1}{20} \\ \end{align}$

Bài 2. (1,5 điểm)

Câu 2:

$\begin{align} & a,2x+\frac{1}{3}=\frac{5}{6} \\ & 2x=\frac{5}{6}-\frac{1}{3} \\ & 2x=\frac{1}{2} \\ & x=\frac{1}{4} \\ \end{align}$

Vậy

$\begin{align} & b,1\frac{2}{3}:x+\frac{3}{7}=-\frac{6}{5} \\ & \frac{5}{3}:x=\frac{-6}{5}-\frac{3}{7} \\ & \frac{5}{3}:x=\frac{-57}{35} \\ & x=\frac{5}{3}:\frac{-57}{35}=\frac{5}{3}.\frac{35}{-57} \\ & x=\frac{-175}{171} \\ \end{align}$

Vậy

c) (x – 5)² = (1 – 3x)².

Trường hợp 1: x – 5 = 1 – 3x.

x + 3x = 1 + 5.

4x = 6.

x = 6 4 x=64 .

x = 3 2 x=32 .

Trường hợp 2: x – 5 = ‒(1 – 3x)

x – 5 = ‒1 + 3x

x ‒ 3x = ‒1 + 5.

‒2x = 4.

x = 4 : (‒2).

x = ‒2.

Vậy x = 3 2 x=32 ; x = ‒2.

Bài 3. (0,75 điểm)

Để tính được số tiền bác Long dùng để sơn căn phòng ta phải tính được diện tích phần cần sơn.

Diện tích phần cần sơn = Diện tích xung quanh của căn phòng – Diện tích các cửa.

Diện tích xung quanh của căn phòng là:

S_xq = 2. (5 + 6) . 3 = 66 (m²).

Diện tích phần cửa lớn và cửa sổ là:

1,2 . 2 + 1 . 1 = 3,4 (m²)

Diện tích phần cần sơn là:

66 – 3,4 = 62,6 (m²).

Tổng chi phí cần để sơn là:

62,6. 30 000 = 1 878 000 (đồng).

Vậy bác Long cần 1 878 000 đồng để sơn bốn bức tường xung quanh của căn phòng này.

Bài 4. (1,5 điểm)

Đổi 3 dm = 30 cm; 4 dm = 40 cm; 5 dm = 50 cm;

1,5 dm = 15 cm; 2 dm = 20 cm; 2,5 dm = 25 cm;

0,45 m = 45 cm.

a) Thể tích của khối gỗ là:

1 2 12 . 40 . 30 . 45 – 1 2 12 . 20 . 15 . 25 = 23 250 (cm³).

b) Diện tích xung quanh của khối kim loại là:

(30 + 40 + 50).45 = 5 400 (cm²).

Diện tích xung quanh của cái lỗ là:

(20 + 15 + 25).45 = 2 700 (cm²).

Diện tích hai đáy trừ đi diện tích hai cái đáy lỗ là:

1 2 12 .30.40 – 1 2 12 .15.20 = 450 (cm²).

Diện tích bề mặt cần sơn là:

5 400 + 2 700 – 450 = 7 650 (cm²) = 0,765 (m²)

Vậy diện tích cần sơn là 0,765 mét vuông.

Bài 5 (1,25 điểm)

a) Hai góc kề bù có trong hình vẽ là góc xOy và góc yOm.

b) Quan sát hình vẽ ta có:

Góc xOy và góc yOm là hai góc kề bù (câu a)

Suy ra: $\widehat {xOy} + \widehat {yOm} = {180^0}$

$\begin{matrix} {60^0} + \widehat {yOm} = {180^0} \hfill \\ \Rightarrow \widehat {yOm} = {180^0} - {60^0} = {120^0} \hfill \\ \end{matrix}$

Vậy góc yOm có số đo là 120⁰

c) Theo bài ra ta có:

Ot là tia phân giác của góc xOy

=> $\widehat {xOt} = \widehat {yOt} = \frac{{\widehat {xOy}}}{2} = \frac{{{{60}^0}}}{2} = {30^0}$

Ta có:

$\widehat {tOm} = \widehat {yOm} + \widehat {yOt} = {120^0} + {30^0} = {150^0}$

(Hay $\widehat {tOm} = {180^0} - \widehat {xOt} = {180^0} - {30^0} = {150^0}$ )

Bài 6 (0,5 điểm)

Theo phương án 2 ta có: Số tiền nhận được vào ngày thứ nhất là 3 đồng; ngày thứ hai là 3 . 3 = 3² đồng; ngày thứ ba là 3² . 3 = 3³ đồng; … ; ngày thứ mười bảy là 3¹⁷ đồng.

Như vậy số tiền công nhận được theo phương án 2 là:

T = 3 + 3² + 3³ + … + 3¹⁷

Suy ra 3T = 3 . (3 + 3² + 3³ + … + 3¹⁷)

= 3. 3 + 3. 3² + 3 . 3³ + … + 3 . 3¹⁷

= 3² + 3³ + 3⁴ + … + 3¹⁸

Do đó 3T – T = (3² + 3³ + 3⁴ + … + 3¹⁸) – (3 + 3² + 3³ + … + 3¹⁷)

Hay 2T = 3¹⁸ – 3 = 387 420 489 – 3 = 387 420 486 (đồng)

Suy ra T = 193 710 243 (đồng) > 170 000 000 (đồng).

Vậy nhóm kĩ thuật viên nên chọn phương án 2 để nhận được nhiều tiền công hơn.

III. Đề kiểm tra giữa kì 1 Toán 7 Kết nối tri thức với cuộc sống

1. Khung ma trận đề kiểm tra giữa kì 1 Toán 7 KNTT

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá								Tổng điểm
			Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
			TN	TL	TN	TL	TN	TL	TN	TL
1	Số hữu tỉ (14 tiết)	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	3 (0,5đ)		1 (0,25đ)						4
1	Số hữu tỉ (14 tiết)	Các phép toán với số hữu tỉ				1 (0,5đ)		4 (2 đ)		1 (0,5đ)	4
2	Số thực (10 tiết)	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	2 (0,5đ)			1 (1đ)					3
2	Số thực (10 tiết)	Tập hợp các số thực	2 (0,5đ)					2 (1 đ)			3
3	Góc và đường thẳng song song (11 tiết)	Góc ở vị trí đặc biệt. Tia phân giác của một góc	2 (0,5đ)					1 (0,5đ)			3
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	1 (0,25đ)					2 (1đ)
		Định lí và chứng minh định lí	1 (0,25đ)	1 (0,5đ)
Tổng: Số câu Điểm			11 (2,75đ)	1 (0,5đ)	1 (0,25đ)	2 (1,5đ)	0 (0 đ)	9 (4,5đ)	0 (0 đ)	1 (0,5đ)	10
Tỉ lệ			32,5%		1,75%		45%		5%
Tỉ lệ chung			50%				50%

2. Bản đặc tả ma trận đề kiểm tra giữa kì 1 Toán 7 KNTT

STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá	Số câu hỏi theo mức độ
STT	Nội dung kiến thức	Đơn vị kiến thức	Mức độ kiến thức, kĩ năng cần kiềm tra, đánh giá	Nhận biết	Thông hiểu	Vận dụng	Vận dụng cao
1	Số hữu tỉ	Tập hợp các số hữu tỉ. Thứ tự thực hiện các phép tính.	Nhận biết: - Nhận biết được số hữu tỉ. - Nhận biết được tập hợp các số hữu tỉ ℚ. - Nhận biết được số đối của số hữu tỉ. - Nhận biết được thứ tự trong tập hợp số hữu tỉ.	3 (TN1,TN2, TN3)
			Thông hiểu: - Biểu diễn số hữu tỉ trên trục số.	1 (TN4)
			Vận dụng: - So sánh hai số hữu tỉ.
		Các phép toán với số hữu tỉ	Thông hiểu: - Mô tả được phép tính lũy thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai lũy thừa cùng cơ số, lũy thừa của lũy thừa). - Mô tả được thứ tự thực hiện phép tính, quy tắc dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ.		1 (TL1a)
			Vận dụng: - Thực hiện được các phép tính: cộng, trừ, nhân, chia trong tập hợp số hữu tỉ. - Vận dụng được các tính chất giao hoán, kết hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viết và tính nhẩm, tính nhanh một cách hợp lí). - Giải quyết được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số hữu tỉ (ví dụ: các bài toán liên quan chuyển động trong Vật lí, đo đạc, …).			4 (TL2a, TL2b, TL3a, TL3b)
			Vận dụng cao: - Giải quyết được một số vấn đề thực tiễn (phức hợp, không quen thuộc) gắn với các phép tính về số hữu tỉ. - Tính được tổng dãy số có quy luật.				(TL5)
2	Số thực	Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	Nhận biết: - Nhận biết số thập phân hữu hạn và số thập phân vô hạn tuần hoàn. - Nhận biết số vô tỉ. - Nhận biết căn bậc hai số học của một số không âm.	2 (TN5, TN6)
		Số thập phân vô hạn tuần hoàn. Số vô tỉ. Căn bậc hai số học	Thông hiểu: - Mô tả được cách viết chu kì của số thập phân vô hạn tuần hoàn. - Tính giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số nguyên dương bằng máy tính cầm tay - Làm tròn số căn cứ vào độ chính xác cho trước.		1 (TL1b)
		Tập hợp các số thực	Nhận biết: - Nhận biết số thực, số đối và giá trị tuyệt đối của số thực. - Nhận biết thứ tự trong tập hợp các số thực.	2 (TN7, TN8)
			Thông hiểu: - Biểu diễn số thực trên trục số trong trường hợp thuận lợi.
			Vận dụng: - So sánh hai số thực. - Vận dụng các tính chất và quy tắc để thực hiện các phép tính với số thực (tương tự như số hữu tỉ).			2 (TL2c, TL3c)
3	Góc và đường thẳng song song	Góc ở vị trí đặc biệt. Tia phân giác của một góc	Nhận biết: - Nhận biết hai góc kề bù, hai góc đối đỉnh. - Nhận biết tia phân giác của một góc.	2 (TN9, TN10)
		Góc ở vị trí đặc biệt. Tia phân giác của một góc	Vận dụng: - Vẽ tia phân giác của một góc bằng dụng cụ học tập. - Tính được số đo góc dựa vào tính chất của các góc ở vị trí đặc biệt. - Tính được số đo góc dựa vào tính chất của tia phân giác.			2 (TL4b, TL4c)
		Dấu hiệu nhận biết và tính chất hai đường thẳng song song. Tiên đề Euclid.	Nhận biết: - Nhận biết các góc tạo bởi một đường thẳng cắt hai đường thẳng. - Nhận biết cách vẽ hai đường thẳng song song. - Nhận biết tiên đề Euclid về đường thẳng song song.	1 (TN11)
			Thông hiểu: - Mô tả dấu hiệu nhận biết hai đường thẳng song song thông qua cặp góc đồng vị, cặp góc so le trong. - Mô tả một số tính chất của hai đường thẳng song song.
			Vận dụng: - Chứng minh hai đường thẳng song song. - Tính số đo của góc tạo bởi hai đường thẳng song song.			1 2 (TL4b, TL4c)
		Định lí và chứng minh định lí	Nhận biết: - Nhận biết một định lí, giả thiết, kết luận của định lí.	3 (TN12, TL4a)
			Vận dụng: - Làm quen với chứng minh định lí.

3. Đề thi giữa kì 1 Toán 7 sách KNTT

Câu 1. Khẳng định nào sau đây đúng nhất:

Nếu a ∈ℤ thì

A. a ∈ ℝ;

B. a ∈ℚ;

C. Cả A và B đều đúng.

D. Cả A và B đều sai.

Câu 2: Kết quả của phép tính $\frac{{22}}{4}:\frac{{11}}{8}$ bằng:

A. 1

B. 2

C. 3

D. 4

Câu 3: Giá trị x thỏa mãn $\frac{3}{4}x = \frac{{15}}{{16}}$ là:

A. $x = \frac{{ - 4}}{5}$

B. $x = \frac{4}{5}$

C. $x = \frac{{ - 5}}{4}$

D. $x = \frac{5}{4}$

Câu 4: $\frac{{ - 1}}{6}$ là kết quả của phép tính:

A. $\frac{{22}}{{14}}.\frac{7}{{11}}.\frac{1}{6}$	B. $\frac{3}{4}.\left( {\frac{{ - 7}}{{14}}} \right).\frac{4}{{21}}$
C. $\frac{5}{{16}}.\frac{8}{{15}}.2$	D. $\frac{{ - 4}}{{12}}.\left( {\frac{{ - 5}}{6}} \right).\left( {\frac{{ - 9}}{{15}}} \right)$

Câu 5. Trong các số sau đây số nào là số thập phân vô hạn không tuần hoàn:

A. 1,(3);

B. 1,2(21);

C. 1,11111…;

D. 2,64575…

Câu 6. Căn bậc hai số học của số a không âm là:

A. √ a ;

B. − √ a ;

C. √ a và − √ a

D. Không có đáp án.

Câu 7. Cho x = -12. Tính |x + 2|.

A. 10;

B. -10;

C. 12;

D. -12.

Câu 8. Khẳng định nào sau đây là đúng?

A. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm trước điểm 0, cách 0 một đoạn bằng √ 3 3 trên trục số;

B. Chỉ có một giá trị x thỏa mãn x² = 3 được biểu diễn bởi điểm nằm sau điểm 0, cách 0 một đoạn bằng √ 3 3 trên trục số;

C. Có hai giá trị x thỏa mãn x² = 3 được biểu diễn bởi hai điểm, một điểm nằm trước và một điểm nằm sau điểm 0, hai điểm đều cách điểm 0 một khoảng bằng √ 3 3 trên trục số;

D. Không có giá trị nào của x thỏa mãn x² = 3.

Câu 9. Cho hình vẽ sau:

Đề thi Giữa kì 1 Toán lớp 7 Kết nối tri thức có đáp án (4 đề + ma trận)

Số cặp góc kề bù (không kể góc bẹt) có trong hình vẽ trên là

A. 1;

B. 2;

C. 3;

D. 4.

Câu 10. Cho ˆ x O y = 120 ° xOy^=120° , tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:

A.120°;

B. 80°;

C. 60°;

D.150°.

Câu 11. Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:

A. Hai đường thẳng đó trùng nhau;

B. Hai đường thẳng cắt nhau tại A;

C. Hai đường thẳng song song;

D. Hai đường thẳng vuông góc.

Câu 12. Định lí sau được phát biểu thành lời là:

Giả thiết	a // b, c ⊥ a
Kết luận	c ⊥ b

A. Nếu một đường thẳng vuông góc một trong hai đường thẳng song song thì nó vuông góc với đường thẳng kia.

B. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó song song với đường thẳng kia.

C. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc 60⁰.

D. Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó tạo với đường thẳng kia một góc 180⁰.

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Biết biểu thức 6⁸. 12⁵ viết được dưới dạng 2^a. 3^b. Tính a – b.

b) Cho a = $√ 99$ = 9,94987471… và b = 5,(123).

i) Hai số b là số thập phân hữu hạn, số thập phân vô hạn tuần hoàn hay số vô tỉ? Tìm chữ số thập phân thứ năm của số b.

ii) Ước lượng tích của a và b.

Bài 2. (1,5 điểm) Thực hiện phép tính (bằng cách hợp lí nếu có thể)

$a. 1\frac{3}{5}.\frac{4}{7}+5\frac{2}{3}.\frac{4}{7}$	$b. \frac{3}{8}+\left( \frac{3}{4}-1\frac{1}{5} \right):\frac{16}{5}$
$c. {{\left( \frac{-4}{3} \right)}^{3}}:\frac{{{\left( \frac{-1}{3} \right)}^{2}}}{6}$

Bài 3. (1,5 điểm) Tìm x biết:

$a. \left( x-2 \right)\left( 3-2x \right)=0$
$b. \frac{1}{3}+\frac{2}{3}:x=5$

c) 7,2 : [41 – (2x – 5)] = 2³.5;

Bài 4. (2,0 điểm)

Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho $\widehat {xOz} = 135^\circ$ . Vẽ tia Ot sao cho $\widehat {yOt} = 90^\circ$ và $\widehat {zOt} = 135^\circ$ . Gọi Ov là tia phân giác của $\widehat {xOt}$ . Các góc $\widehat {xOv}$ và $\widehat {yOz}$ có phải là hai góc đối đỉnh không? Vì sao?

Bài 5. (0,5 điểm)

$\frac{1}{2} - \frac{2}{3} + \frac{3}{4} - \frac{4}{5} + \frac{5}{6} - \frac{6}{7} + \frac{7}{8} + \frac{6}{7} - \frac{5}{6} + \frac{4}{5} - \frac{3}{4} + \frac{2}{3} - \frac{1}{2} + 1$

4. Đáp án đề kiểm tra giữa kì 1 lớp 7 sách KNTT

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)

Câu	1	2	3	4	5	6	7	8	9	10	11	12
Đáp án	C	D	D	C	D	A	A	C	B	C	A	A

PHẦN II. TỰ LUẬN (7,0 điểm)

Bài 1. (1,5 điểm)

a) Ta có:

6⁸. 12⁵ = (2 . 3)⁸ . (3. 2²)⁵ = 2⁸ . 3⁸ . 3⁵ . (2²)⁵

= 2⁸ . 2^{2 . 5} . 3^{8 + 5} = 2^{8 + 10} . 3¹³ = 2¹⁸ . 3¹³.

Khi đó a = 18 và b = 13.

Do đó a – b = 18 – 13 = 5.

Vậy a – b = 5.

i) Số b = 5,(123) = 5,12312312… là số thập phân vô hạn tuần hoàn có chu kì là 123.

Chữ số thập phân thứ năm của số b là chữ số 2.

ii) Làm tròn a = √ 99 99 = 9,94987471… đến hàng đơn vị ta được a ≈ 10.

Làm tròn b = 5,12312312… đến hàng đơn vị ta được b ≈ 5.

Khi đó ước lượng tích của a và b là a . b ≈ 10 . 5 = 50.

Bài 2. (1,5 điểm)

$a. 1\frac{3}{5}.\frac{4}{7}+5\frac{2}{3}.\frac{4}{7}=\frac{8}{5}.\frac{4}{7}+\frac{17}{3}.\frac{4}{7}=\frac{4}{7}\left( \frac{8}{5}+\frac{17}{3} \right)=\frac{4}{7}.\left( \frac{24}{15}+\frac{85}{15} \right)=\frac{4}{7}.\frac{109}{15}=\frac{436}{105}$

$b. \frac{3}{8}+\left( \frac{3}{4}-1\frac{1}{5} \right):\frac{16}{5}$

$=\frac{3}{8}+\left( \frac{3}{4}-\frac{6}{5} \right).\frac{5}{16}=\frac{3}{8}+\frac{-9}{20}.\frac{5}{16}=\frac{3}{8}-\frac{9}{64}=\frac{15}{64}$

$c. {{\left( \frac{-4}{3} \right)}^{3}}:\frac{{{\left( \frac{-1}{3} \right)}^{2}}}{6}=\frac{{{\left( -4 \right)}^{3}}}{{{3}^{3}}}.\frac{6}{\frac{1}{{{3}^{2}}}}=-64.6=-384$

Bài 3. (1,5 điểm)

$a. \left( x-2 \right)\left( 3-2x \right)=0 \Rightarrow \left[ \begin{matrix} x-2=0 \\ 3-2x=0 \\ \end{matrix} \right.\Rightarrow \left[ \begin{matrix} x=2 \\ x=-\dfrac{3}{2} \\ \end{matrix} \right.$

Vậy $x=2$ hoặc $x=-\frac{3}{2}$

$b. \frac{1}{3}+\frac{2}{3}:x=5$

$\begin{align} & \frac{1}{3}+\frac{2}{3}:x=5 \\ & \Rightarrow \frac{2}{3}:x=5-\frac{1}{3}=\frac{14}{3} \\ & \Rightarrow \frac{2}{3.x}=\frac{14}{3} \\ & \Rightarrow x=\frac{1}{7} \\ \end{align}$

Vậy $x=\frac{1}{7}$

c) 7,2 : [41 – (2x – 5)] = 2³. 5.

7,2 : [41 – (2x – 5)] = 8 . 5

7,2 : [41 – (2x – 5)] = 40

41 – (2x – 5) = 7,2 : 40

41 – (2x – 5) = 0,18

2x – 5 = 41 – 0,18

2x – 5 = 40,82

2x = 40,82 + 5

2x = 45,82

x = 45,82 : 2

x = 22,91

Vậy x = 22,91.

Bài 4. (2,0 điểm)

Bài 4

Vì $\widehat {yOt} = 90^\circ \Rightarrow Oy \bot Ot \Rightarrow Ox \bot Ot$ nên $\widehat {xOt} = 90^\circ$

Vì Ov là tia phân giác của $\widehat {xOt}$ nên $\widehat {xOv} = \widehat {vOt} = \frac{1}{2}.\widehat {xOt} = \frac{1}{2}.90^\circ = 45^\circ$

Vì $\widehat {vOx} + \widehat {xOz} = 45^\circ + 135^\circ = 180^\circ$ nên Ov và Oz là hai tia đối nhau

Như vậy, các góc $\widehat {xOv}$ và $\widehat {yOz}$ là hai góc đối đỉnh vì Ox là tia đối của tia Oy, tia Ov là tia đối của tia Oz

Bài 5. (0,5 điểm)

$\frac{1}{2} - \frac{2}{3} + \frac{3}{4} - \frac{4}{5} + \frac{5}{6} - \frac{6}{7} + \frac{7}{8} + \frac{6}{7} - \frac{5}{6} + \frac{4}{5} - \frac{3}{4} + \frac{2}{3} - \frac{1}{2} + 1$

$= \left( {\frac{1}{2} - \frac{1}{2}} \right) + \left( { - \frac{2}{3} + \frac{2}{3}} \right) + \left( {\frac{3}{4} - \frac{3}{4}} \right) + \left( { - \frac{4}{5} + \frac{4}{5}} \right)$

$+ \left( {\frac{5}{6} - \frac{5}{6}} \right) + \left( { - \frac{6}{7} + \frac{6}{7}} \right) + \frac{7}{8} + 1$

$= 0 + \frac{7}{8} + 1 = \frac{7}{8} + \frac{8}{8} = \frac{{15}}{8}$

IV. Đề thi giữa học kì 1 Toán 7 Cánh diều

1. Ma trận đề thi giữa kì 1 Toán 7 Cánh diều

TT	Chủ đề	Nội dung/Đơn vị kiến thức	Mức độ đánh giá								Tổng % điểm
			Nhân biết		Thông hiểu		Vân dung		Vân dung cao
			TNKQ	TL	TNKQ	TL	TNKQ	TL	TNKQ	TL
1	Số hữu tỉ (12T)	Số hữu tỉ và tập hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ (4 T)	1- ( 0,2- C1)		1-(0,2-C 2)						4
		Các phép tính với số hữu tỉ (8 T)			2- (0,4 - C 3;4)	2- (1,0(B1a,b)		2-(1,0 B 2ab)		2- (1,0 B5a;b)	34
2	Số thực (10 T)	Căn bậc hai số học (1T)	1- (0,2 C5)								2
		Số vô tỉ. Số thực (1T)	1-(0,2 C 6)								2

		Tỉ lệ thức. Tính chất của dãy tỉ số bằng nhau. (8T)	4- (0,8- C7,8,9,10)					1-( 2,0 ( B3)		28
3	Các hinh hinh hoc cơ ban (10T)	Góc ở vị trí đặc biệt. Tia phân giác của một góc (3T)	1- (0,2 C13)	1-(0,5B 4a)						7
		Hai đường thẳng song song. Tiên đề Euclid về đường thẳng song song (7T)	2–(0,4Câu 11;15)		2-(0,4 C 12,14)	2-(1,5 B 4bc)				23
Tổng			2,0	0,5	1,0	2,5		3	1	22
Tỉ lệ %			20%	5%	10%	25%		30%	10%	100
Tỉ lệ chung			60%				40%			100

2. Bản đặc tả đề kiểm tra giữa kì 1 Toán 7 sách Cánh diều

T T	Chủ đề		Mức độ đánh giá	Số câu hỏi theo mức độ nhân thức
T T	Chủ đề		Mức độ đánh giá	Nhân biết	Thông hiểu	Vân dung	Vân dung cao
ĐẠI SỐ
1	Số hữu tỉ	Số hữu tỉ và tập	Nhân biết:	(TN1)	(TN1)

hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ	– Nhận biêt được số hữu tỉ và lấy được ví du về số hữu tỉ. – Nhận biêt được tập hợp các số hữu tỉ. – Nhận biêt được số đối của một số hữu tỉ. – Nhận biêt được thứ tự trong tập hợp các số hữu tỉ.
hợp các số hữu tỉ. Thứ tự trong tập hợp các số hữu tỉ	Thông hiểu: – Biểu diễn được số hữu tỉ trên truc số.
Các phép tính với số hữu tỉ	Thông hiểu: – Mô tả được phép tính luỹ thừa với số mũ tự nhiên của một số hữu tỉ và một số tính chất của phép tính đó (tích và thương của hai luỹ thừa cùng cơ số, luỹ thừa của luỹ thừa). – Mô tả được thứ tự thực hiện các phép tính, quy tắc dấu ngoặc, quy tắc chuyển vê trong tập hợp số hữu tỉ.	(TL2)
Các phép tính với số hữu tỉ	Vân dung: – Thực hiện được các phép tính:		(TN 3,4)	1 (TL 5)

cộng, trừ, nhân, chia trong tập hợp số hữu tỉ.

– Vận dung được các tính chất giao hoán, kêt hợp, phân phối của phép nhân đối với phép cộng, quy tắc dấu ngoặc với số hữu tỉ trong tính toán (tính viêt và tính nhâm, tính nhanh một cách hợp lí).

– Giải quyêt được một số vấn đề thực tiễn (đơn giản, quen thuộc) gắn với các phép tính về số hữu tỉ. (ví du: các bài toán liên quan đên chuyển động trong Vật lí, trong đo đạc,...).

Số thực

Căn bậc hai số học Số vô tỉ. Số thực

Nhân biết:

– Nhận biêt được khái niệm căn bậc hai số học của một số không âm.

(TN 5)

(TN 6)

Tỉ lệ thức. Tính chất của dãy tỉ số bằng nhau.

Vân dung:

– Vận dung được tính chất của tỉ lệ thức trong giải toán.

– Vận dung được tính chất của dãy tỉ số bằng nhau trong giải toán (ví du: chia một số thành các phần tỉ lệ với

các số cho trước,...).

5 (TL)

(TN 7,8,9,10)

5	Các hinh hinh học cơ bản	Góc ở vị trí đặc biệt. Tia phân giác của một góc Hai đường thẳng song song. Tiên đề Euclid về đường thẳng song song	Nhân biết: – Nhận biêt được tiên đề Euclid về đường thẳng song song. Thông hiểu: – Mô tả được một số tính chất của hai đường thẳng song song. – Mô tả được dấu hiệu song song của hai đường thẳng thông qua cặp góc đông vị, cặp góc so le trong.	3 (TL4a) (TN 11,13,15)	3 (TN 12,14) (TL 4b)	2 (TN14) (TL 4c)
TỔNG				2,5	3,5	3	1
TỶ LỆ %				25%	35%	30%	10%
TỶ LỆ CHUNG				60%		40%

3. Đề thi giữa kì 1 Toán 7 sách Cánh diều

PHẦN I. TRẮC NGHIỆM (3,0 điểm).

Chọn đáp án đúng trong các câu sau:

Câu 1. NB. Số đối của $\frac{-2}{3}$ là

Đề Toán 7 giữa kì 1 Cánh diều

Câu 2. TH. Cách biểu diễn số trên trục số nào dưới đây đúng.

Đề Toán 7 giữa kì 1 Cánh diều

Câu 3. NB. Số đối của $4\frac{1}{3}$ ; $\sqrt{5}$ ; $-\sqrt{44}$ lần lượt là

Đề Toán 7 giữa kì 1 Cánh diều

Câu 4. TH. Giá trị của biểu thức 2⁵ . $\frac{1}{_{2}2 }$ là

A. 1.

B. 8.

C. 9²

D. 9⁴

Câu 5. NB. Trong các cách viết sau, cách viết nào biểu diển số hữu tỉ?

Đề Toán 7 giữa kì 1 Cánh diều

Câu 6. NB. Các mặt bên của hình lăng trụ đứng ABCD.A'B'C'D' có mặt BB'C'C là

Đề Toán 7 giữa kì 1 Cánh diều

A. Các hình bình hành.

C. Các hình chữ nhật.

B. Các hình thang cân.

D. Các hình vuông.

Câu 7. NB. Hình lăng trụ đứng tam giác có số cạnh là

A. 8 .

B. 12

C. 9

D. 10

Câu 8. NB. Hình hộp chữ nhật có mặt là hình gì?

A. Hình vuông.

B. Hình chữ nhật.

C. Hình bình hành.

D. Hình thoi.

Câu 9. NB. Công thức tính diện tích xung quanh của hình hộp chữ nhật với chiều dài là, chiều rộng là, chiều cao là (cùng đơn vị đo) là:

Đề Toán 7 giữa kì 1 Cánh diều

Còn tiếp.............

Tham khảo toàn bộ đề và đáp án Đề kiểm tra giữa kì 1 Toán 7 sách Cánh diều năm 2022 tại đây: Đề thi giữa kì 1 Toán 7 năm 2022 sách Cánh diều

V. Đề thi giữa học kì 1 lớp 7 Tải nhiều

-------

Để chuẩn bị tốt cho kì thi giữa học kì 1 lớp 7 môn Toán sắp tới, VnDoc giới thiệu tới các bạn chuyên mục Đề thi giữa kì 1 lớp 7 với đầy đủ các môn. Đây là tài liệu hay cho thầy cô tham khảo ra đề, cũng là nguồn tài liệu để các em học sinh ôn luyện trước kì thi. Mời thầy cô và các em tham khảo.

Đánh giá bài viết

29 19.065

Bài trước

Bài sau