Định lý
Chuyên đề Toán học lớp 7: Định lý được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Định lý
A. Lý thuyết
1. Định lí. Giả thiết và kết luận của định lí
+ Một tính chất được khẳng định là đúng bằng suy luận gọi là một định lí
+ Giả thiết của định lú là điều cho biết. Kết luận của định lí là điều được suy ra
2. Chứng minh định lý
Chứng minh định lí là dung lập luận để từ giả thiết suy ra kết luận
Ví dụ: Cho định lý: “Nếu hai đường thẳng cùng song song với đường thẳng thứ ba thì hai đường thẳng song song” . Khi đó giả thiết – kết luận được ghi lại như sau
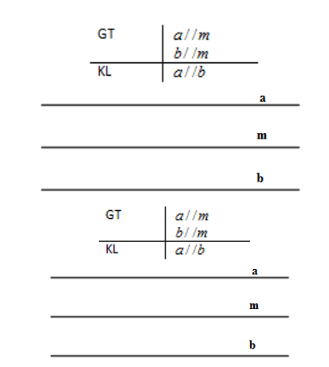
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Chứng minh định lý là:
A. Dùng lập luận để từ giả thiết suy ra kết luận
B. Dùng hình vẽ để từ giả thiết suy ra kết luận
C. Dùng đo đạc thực tế để từ giả thiết suy ra kết luận
D. Cả A, B, C đều sai
Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận
Chọn đáp án A.
Bài 2: Trong các câu sau, câu nào cho một định lý:
A. Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.
B. Đường thẳng nào vuông góc với một trong hai đường thẳng cắt nhau thì song song với đường thẳng kia.
C. Nếu hai đường thẳng và cùng song song với một đường thẳng thứ ba thì hai đường thẳng đó song song.
D. Nếu hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì hai đường thẳng đó song song.
Định lý: “Đường thẳng nào vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng kia.”
Chọn đáp án A.
Bài 3: Cho định lý: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau” (xem hình vẽ dưới đây). Giả thiết của định lý là:
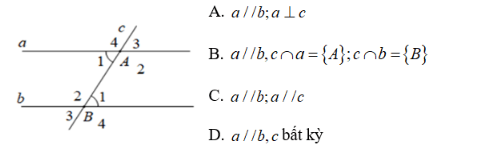
Giả thiết của định lý trên là: a // b, c ∩ a = {A}, c ∩ b = {B}
Chọn đáp án B.
Bài 4: Chọn định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông” (hình vẽ). Giả thiết, kết luận của định lý là:
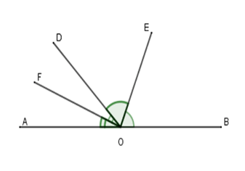
A. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OE ⊥ OF
B. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOF, OF là phân giác góc AOD. Kết luận: OE ⊥ OA
C. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOE. Kết luận: OE ⊥ OF
D. Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD. Kết luận: OB ⊥ OF
Giả thiết: Cho góc bẹt AOB và tia OD, OE là phân giác góc BOD, OF là phân giác góc AOD.
Kết luận: OE ⊥ OF
Chọn đáp án A.
Bài 5: Phần giả thiết:![]() (tham khảo hình vẽ) là của định lý nào dưới đây:
(tham khảo hình vẽ) là của định lý nào dưới đây:
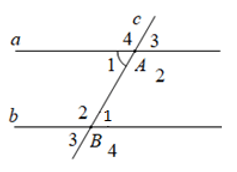
A. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc ngoài cùng phía bù nhau thì hai đường thẳng đó song song.
B. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc so le trong bù nhau thì hai đường thẳng đó song song.
C. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau thì hai đường thẳng đó song song.
D. Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Nếu hai đường thẳng cắt một đường thẳng thứ ba tạo thành hai góc trong cùng phía bù nhau thì hai đường thẳng đó song song.
Chọn đáp án D.
II. Bài tập tự luận
Bài 1: Điền vào chỗ trống những nội dung thích hợp để được các định lí đúng
a) Nếu M là trung điểm của đoạn AB thì ....
b) Nếu .... thì MA = MB = (1/2)AB
c) Nếu tia Ot là tia phân giác của góc xOy thì ....
a) Có thể điền vào chỗ trống vài cách sau đây:
+ M nằm giữa A và B
+ MA = MB
+ MA = MB = (1/2)AB
+ M nằm giữa A, B và
+ MA + MB = AB và MA = MB
b) Chỉ có thể điền vào chỗ trống: M là trung điểm của AB
c) Có thể điền vào chỗ trống vài cách sau đây:
+ Ot nằm giữa hai tia Ox và Oy
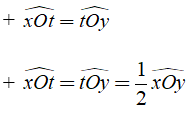
Bài 2: Chứng minh định lý: “Hai tia phân giác của hai góc kề bù vuông góc với nhau”.
Đáp án
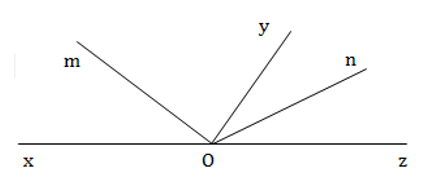
Gọi 2 góc kề bù là ∠xOy và ∠yOz , có lần lượt hai tia phân giác là Om và On
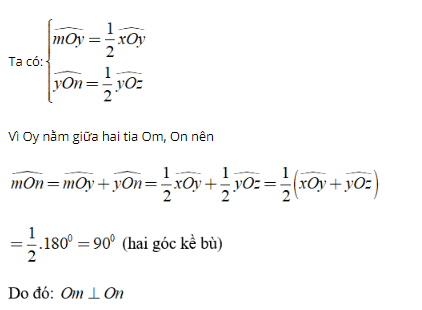
Vậy hai tia phân giác của hai góc kề bù vuông góc với nhau.
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 7: Định lý. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc







