Nghiệm của đa thức một biến

Chuyên đề Toán học lớp 7: Nghiệm của đa thức một biến được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.

1. Nghiệm của đa thức một biến là gì?

Nếu tại x = a, đa thức P(x) có giá trị bằng 0 thì ta nói a (hoặc x = a) là một nghiệm của đa thức đó.

Chú ý:

+ Một đa thức (khác đa thức không) có thể có một nghiệm, hai nghiệm,… hoặc không có nghiệm.

+ Số nghiệm của một đa thức (khác đa thức không) không vượt quá bậc của nó. Chẳng hạn: đa thức bậc nhất chỉ có một nghiệm, đa thức bậc hai không quá hai nghiệm,…

Ví dụ: Tìm nghiệm của đa thức P(x) = 2y + 6

Từ 2y + 6 = 0 ⇒ 2y = -6 ⇒ y = -3

Vậy nghiệm của đa thức P(x) là -3.

2. Trắc nghiệm Nghiệm của đa thức một biến

Bài 1: Cho đa thức f(x) = 2x² + 12x + 10. Trong các số sau, số nào là nghiệm của đa thức đã cho:

A. -9 B. 1 C. -1 D. -4

f(-9) = 2.(-9)² + 12.(-9) + 10 = 64 ≠ 0 ⇒ x = -9 không là nghiệm của f(x)

f(1) = 2.(1)² + 12.(1) + 10 = 24 ≠ 0 ⇒ x = 1 không là nghiệm của f(x)

f(-1) = 2.(-1)² + 12.(-1) + 10 = 0 ⇒ x = 1 là nghiệm của f(x)

f(-4) = 2.(-4)² + 12.(-4) + 10 = -6 ≠ 0 ⇒ x = -4 không là nghiệm của f(x)

Chọn đáp án C

Bài 2: Cho các giá trị của x là 0; -1; 1; 2; -2. Giá trị nào của x là nghiệm của đa thức P(x) = x² + x - 2

A. x = 1; x = -2

B. x = 0; x = -1; x = -2

C. x = 1; x = 2

D. x = 1; x = -2; x = 2

P(0) = 0² + 0 - 2 = -2 ≠ 0 ⇒ x = 0 không phải là nghiệm của P(x)

P(-1) = (-1)² + 1.(-1) - 2 = -2 ≠ 0 ⇒ x = -1 không là nghiệm của P(x)

P(1) = 1² + 1.1 - 2 = 0 ⇒ x = 1 là nghiệm của P(x)

P(2) = 2² + 1.2 - 2 = 4 ≠ 0 ⇒ x = 2 không là nghiệm của P(x)

P(-2) = (-2)² + 1.(-2) - 2 = 0 ⇒ x = -2 không là nghiệm của P(x)

vậy x = 1; x = -2 là nghiệm của P(x)

Chọn đáp án A

Bài 3: Tập nghiệm của đa thức f(x) = (x + 14)(x - 4) là:

A. {4; 14} B. {-4; 14} C. {-4; -14} D. {4; -14}

Vậy tập nghiệm của đa thức f(x) là {4; -14}

Chọn đáp án D

Bài 4: Cho đa thức sau f(x) = x² + 5x - 6. Các nghiệm của đa thức đã cho là:

A. 2 và 3 B. 1 và - 6 C. -3 và -6 D. -3 và 8

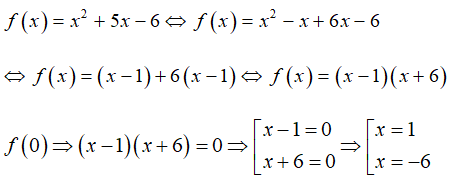
Vậy nghiệm của đa thức f(x) là 1 và -6

Chọn đáp án B

Bài 5: Tổng các nghiệm của đa thức x² - 16 là:

A. -16 B. 8 C. 4 D. 0

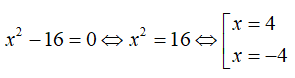
Vậy x = 4; x = -4 là nghiệm của đa thức x² - 16

Tổng các nghiệm là 4 + (-4) = 0

Chọn đáp án D

Bài 6: Số nghiệm của đa thức x³ + 27 là:

A. 1 B. 2 C. 0 D. 3

Ta có x³ + 27 = 0 ⇒ x³ = -27 ⇒ x³ = (-3)³ ⇒ x = -3

Vậy đa thức đã cho có một nghiệm x = -3

Chọn đáp án A.

3. Bài tập tự luận Nghiệm của đa thức một biến

Bài 1: Chứng tỏ các đa thức sau không có nghiệm

a) P(x) = x² + 1 b) Q(y) = 2y⁴ + 5

Đáp án

a) Vì x² ≥ 0 nên x² + 1 ≥ 1

Do đó: P(x) = x² + 1 > 0 nên đa thức P(x) vô nghiệm.

b) Vì y⁴ ≥ 0 nên 2y⁴ + 5 > 0

Do đó: Q(y) = 2y⁴ + 5 > 0 nên đa thức Q(x) vô nghiệm.

Bài 2: Tìm nghiệm của đa thức

a) x² - 2003x - 2004 = 0

b) 2005x² - 2004x - 1 = 0

Đáp án

a) Đa thức x² - 2003x - 2004 = 0 có hệ số a = 1, b = -2003, c = -2004

Khi đó ta có: a - b + c = 1 - (-2003) + (-2004) = 0

Nên đa thức x² - 2003x - 2004 = 0 có nghiệm x = -1

b) Đa thức 2005x² - 2004x - 1 = 0 có hệ số a = 2005, b = -2004, c = -1

Khi đó ta có: a + b + c = 2005 - 2004 - 1 = 0

Nên đa thức 2005x² - 2004x - 1 = 0 có nghiệm x = 1.

Bài tham khảo thêm:

• Bài tập Nghiệm của đa thức một biến
• Trắc nghiệm Nghiệm của đa thức một biến
• Toán 7 Bài 2: Đa thức một biến - Nghiệm của đa thức một biến